Кинематика. Основные понятия

Краткая историческая справка
Развитие кинематики как науки началось еще в древнем мире и связано с таким именем как Галилей , который вводит понятие ускорения . Развитие кинематики в XVIII в. связано с работами Эйлера, заложившего основы кинематики твердого тела и создавшего аналитические методы решения задач механики. Более глубокие исследования геометрических свойств
Более глубокие исследования геометрических свойств движения тела были вызваны развитием техники в начале XIX в. и, в частности, быстрым развитием машиностроения.
Крупные исследования в области кинематики механизмов и машин принадлежат и русским ученым: основоположнику русской школы теории машин и механизмов П.Л. Чебышеву(1821-1894), Л.В. Ассуру (1878-1920), Н.И. Мерцалову (1866-1948), Л.П.Котельникову (1865-1944) и другим ученым.

Основные понятия кинематики:
Кинематика (с греч. κινειν — двигаться) - раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Основная задача кинематики:
зная закон движения данного тела, определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности.

Кинематика - это описание движения тел с математическими ответами на вопросы:
Где?
Когда?
Как?

Основные понятия кинематики:
Материальная точка
Механическое движение
Система отсчета
Траектория
Путь
Перемещение
Скорость
Ускорение

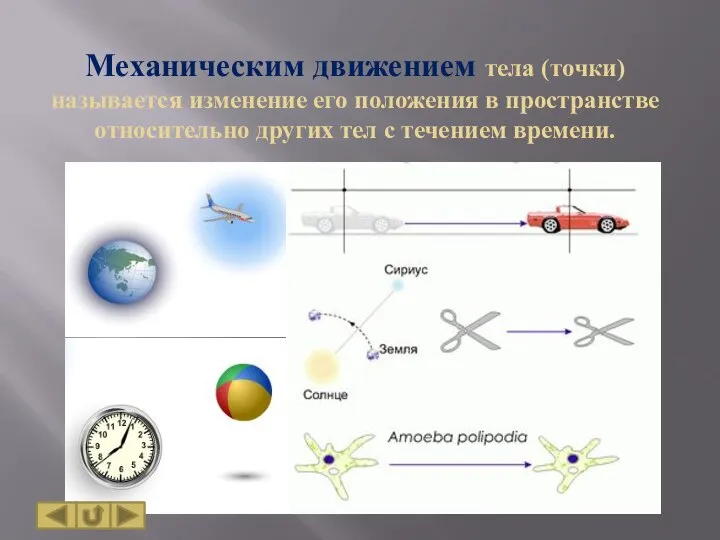
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

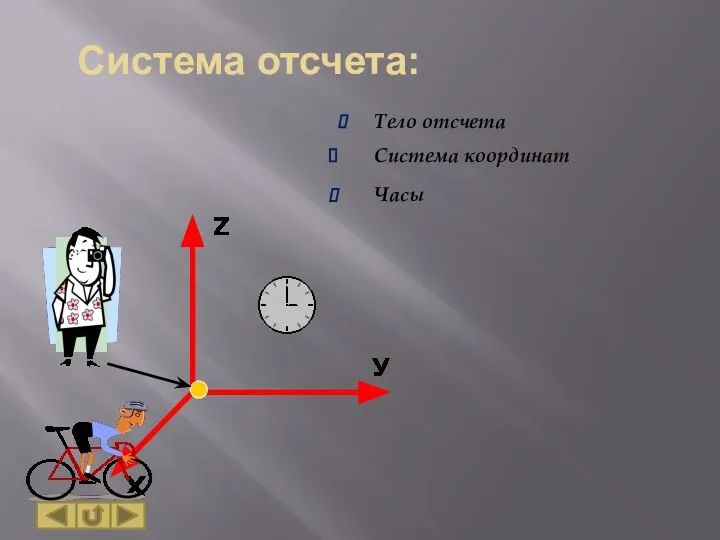
Система отсчета:
Тело отсчета
Система координат
Часы

Материальная точка
Тело можно считать материальной точкой, если:
1. расстояния, проходимые телом, значительно больше размеров этого тела;
2. тело движется поступательно, т.е. все его точки движутся одинаково в любой момент времени.

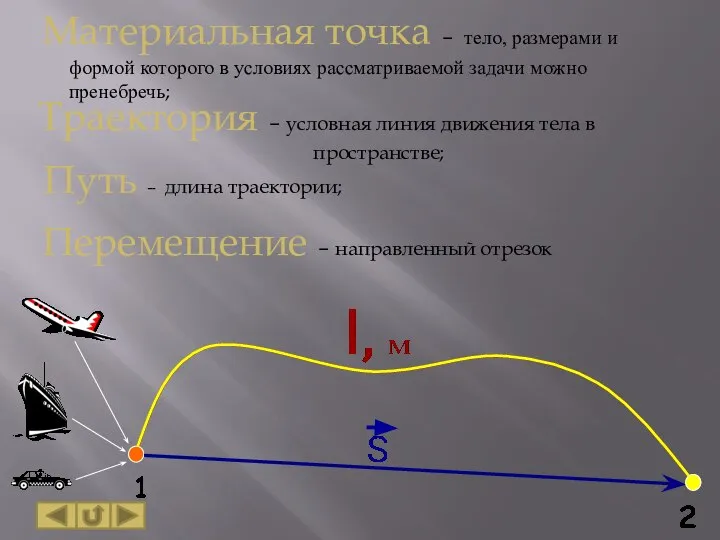
Материальная точка – тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь;
Траектория – условная линия движения тела в пространстве;
Путь – длина траектории;
Перемещение – направленный отрезок

Способы задания движения точки
естественный
При этом способе задают: траекторию точки и закон движения по этой траектории
Положение точки относительно некоторой системы отсчета задано ее координатами
Уравнения движения точки в прямоугольных координатах
x = f 1 (t ) , y = f 2 (t ) , z = f 3 (t )
координатный

Скорость:
скорость неравномерного движения:
скорость равномерного движения –
Направление скорости при:
прямолинейном движении – неизменно
криволинейном движении – по касательной к траектории в
данной точке
векторная величина характеризует быстроту движения, показывает, какое перемещение тело совершает в единицу времени
Движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. называют ПРЯМОЛИНЕЙНЫМ РАВНОМЕРНЫМ.
Движение, при котором за равные промежутки времени тело совершает неравные перемещения называют неравномерным или переменным.
[м/с]

Ускорение -
величина, характеризующая изменение
скорости при неравномерном движении тела. Средним ускорением неравномерного движения в интервале от t до t + ∆t называется векторная величина, равная отношению изменения скорости ∆v к интервалу времени ∆t:

Составляющая аτ вектора ускорения, направленная вдоль касательной к траектории в данной точке, называется тангенциальным (касательным) ускорением. Тангенциальное ускорение характеризует изменение вектора скорости по модулю. Вектор аτ направлен в сторону движения точки при возрастании ее скорости (рисунок - а) и в противоположную сторону - при убывании скорости (рисунок - б).
а
б

Тангенциальная составляющая ускорения аτ равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю:
Вторая составляющая ускорения, равная:
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют так же центростремительным ускорением).
Полное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих:

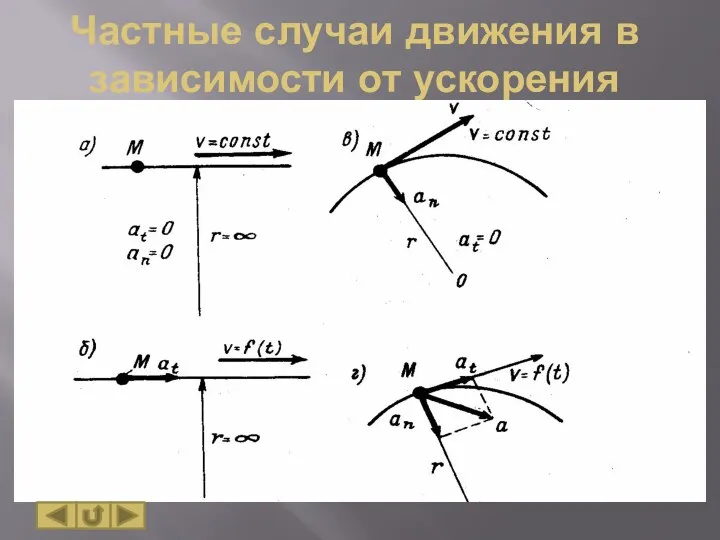
Частные случаи движения в
зависимости от ускорения

Равномерное Равноускоренное движение движение
Графиком перемещения будет являться парабола

Равномерное Равноускоренное движение движение

Равномерное Равноускоренное движение движение

ЗАКРЕПЛЕНИЕ МАТЕРИАЛА