Слайд 2Двойной маятник:
оптимальное управление раскачиванием и торможением
Лекция 1
Гимнаст раскачивается на перекладине,

управляя, в основном, углом в тазобедренном суставе; момент в запястном суставе при этом весьма мал.
Человек управляет колебаниями качелей вокруг точки подвеса, перемещаясь на них подходящим образом, в то время как в точке подвеса качелей отсутствует какой-либо «внешний» управляющий момент. В обоих последних случаях человек надлежащим образом использует силу тяжести.
Животные, человек могут перемещать “звенья” своего тела только одно относительно другого. Однако делают они это так, чтобы внешние силы, возникающие при относительном движении, – силы взаимодействия с окружающей средой, гравитационные силы – осуществляли движение тела как целого желаемым образом.
Например, ходьба, бег животных, ползание пресмыкающихся происходит благодаря силам трения с опорной поверхностью. Животные “организуют” надлежащие воздействия этих внешних сил при относительном движении звеньев тела.
Слайд 4Уравнения движения двойного маятника

Слайд 5Кинетическая энергия:
Потенциальная энергия:
Обобщенная работа:
Уравнения Лагранжа:
- момент инерции жесткого двухзвенника
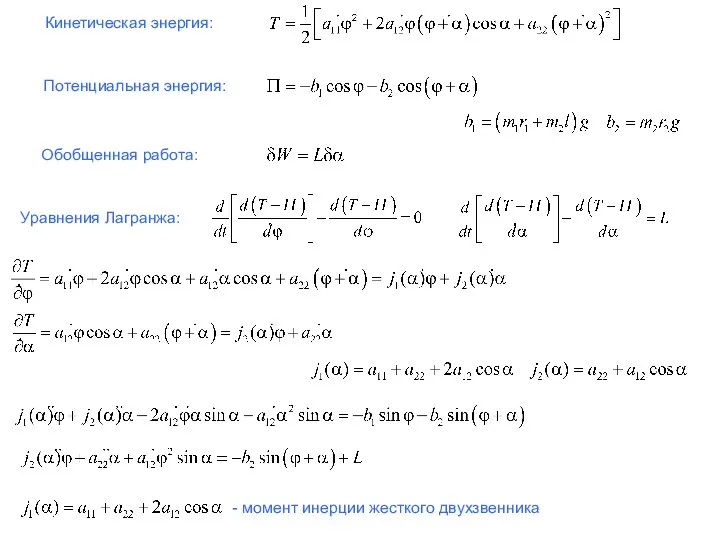
Слайд 9Вместо угла ϕ введем новую переменную p:
Приведённый угол
Если
то
поскольку

Слайд 10Оптимальное управление, раскачивающее маятник
Начальное состояние:
Если
то
Постановка задачи:
Если
то
и

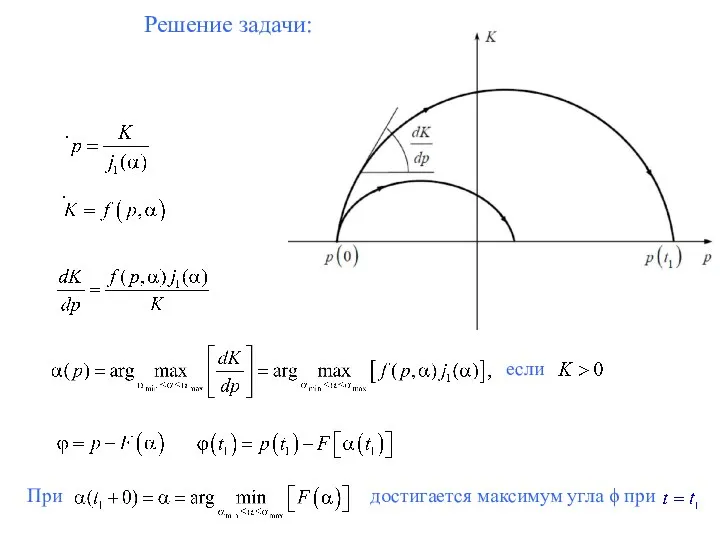
Слайд 11Решение задачи:
если
При
достигается максимум угла ϕ при


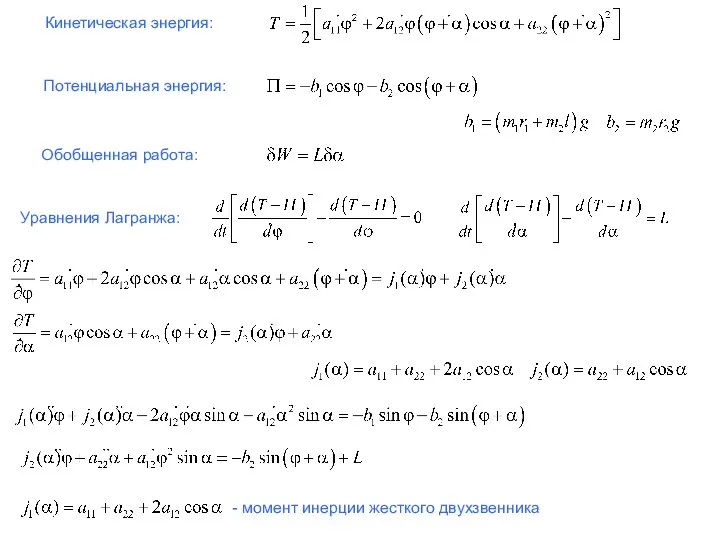





 מצגת חתכים נוספת
מצגת חתכים נוספת Мир в ультрафиолетовых лучах
Мир в ультрафиолетовых лучах Подготовка к ЕГЭ. Решение задач
Подготовка к ЕГЭ. Решение задач Равновесие сил с учётом трения покоя, сцепления
Равновесие сил с учётом трения покоя, сцепления Ускорение
Ускорение Презентация на тему Решение задач импульс, работа. энергия
Презентация на тему Решение задач импульс, работа. энергия  Основы ядерной электроники
Основы ядерной электроники Соединения заформовкой
Соединения заформовкой Проверочные вопросы по теме Этапы работы над исследовательским проектом
Проверочные вопросы по теме Этапы работы над исследовательским проектом Тепловые явления
Тепловые явления Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие проводников с током
Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие проводников с током Физика. Вводная лекция
Физика. Вводная лекция Методы получения изображений видимого излучения
Методы получения изображений видимого излучения Тест по теме: Электромагнитное поле
Тест по теме: Электромагнитное поле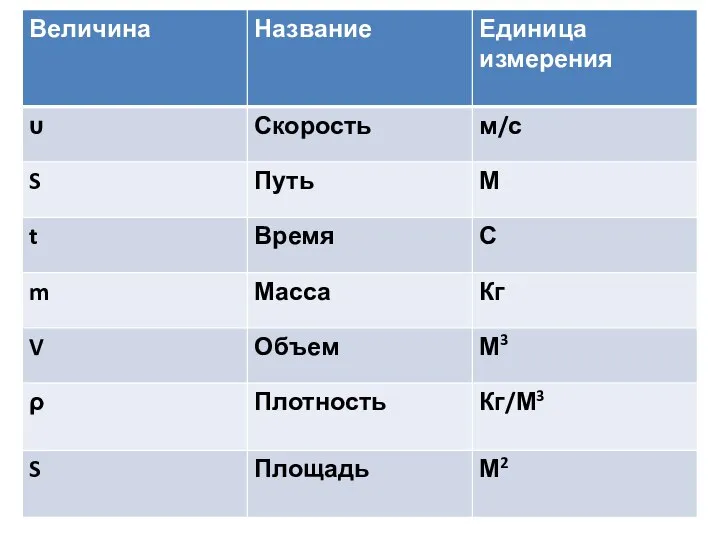 Формулы и величины
Формулы и величины Расчет давления в жидкости
Расчет давления в жидкости Тепловые явления в природе
Тепловые явления в природе Тройная точка воды
Тройная точка воды Проект по фізиці. Шлях, який проходить вчитель за день
Проект по фізиці. Шлях, який проходить вчитель за день Импульс тела
Импульс тела Закон сохранения импульса
Закон сохранения импульса Презентация на тему Спектроскоп
Презентация на тему Спектроскоп  Презентация на тему Единицы массы
Презентация на тему Единицы массы  Прямолинейное равноускоренное движение. Ускорение
Прямолинейное равноускоренное движение. Ускорение Механические колебания. 9 класс
Механические колебания. 9 класс Зонная структура примесных полупроводников. Примесная проводимость. Типы примесных состояний
Зонная структура примесных полупроводников. Примесная проводимость. Типы примесных состояний brounovskoe_dvizhenie
brounovskoe_dvizhenie Презентация на тему Электромагнитные колебания
Презентация на тему Электромагнитные колебания