Содержание
- 2. Основы теории автоматического управления Теория автоматического управления - наука, которая изучает процессы управления, методы их исследования
- 3. Классификация САУ (САР) Все системы автоматического управления и регулирования делятся на следующие основные классы: 1 .По
- 4. Основные понятия ТАУ Параметры технологического процесса - это физические величины, определяющие ход технологического процесса (напряжение, сила
- 5. Основные понятия ТАУ Мгновенное значение – это значение регулируемой величины в рассматриваемый момент времени. Измеренное значение
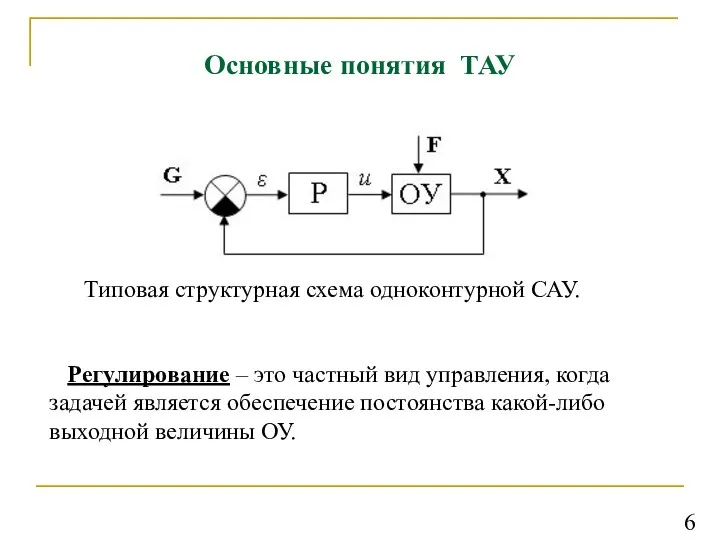
- 6. Основные понятия ТАУ Регулирование – это частный вид управления, когда задачей является обеспечение постоянства какой-либо выходной
- 7. Основные понятия ТАУ Регулирование – это частный вид управления, когда задачей является обеспечение постоянства какой-либо выходной
- 8. Основные понятия ТАУ G – задающее воздействие (входное воздействие Х) – воздействие на систему, определяющее заданный
- 9. Основные понятия ТАУ Р – регулятор, это комплекс устройств, присоединяемых к регулируемому объекту и обеспечивающих автоматическое
- 10. Классификация САР 1. По назначению (по характеру изменения задания): - стабилизирующая САР, это система, алгоритм функционирования
- 11. Классификация САР 2. По количеству контуров: - одноконтурные - содержащие один контур, - многоконтурные - содержащие
- 12. Классификация САР 4. По функциональному назначению: - температуры; - давления; - расхода; - уровня; - напряжения
- 13. Классификация САР Принцип суперпозиции (наложения): Если на вход объекта подается несколько входных воздействий, то реакция объекта
- 14. Классификация элементов САР 1. По функциональному назначению: - измерительные, - усилительно-преобразовательные, - исполнительные, - корректирующие. 2.
- 15. Классификация элементов САР 3. По наличию или отсутствию вспомогательного источника энергии: - активные (с источником энергии),
- 16. Классификация элементов САР 5. По поведению в статическом режиме: - статические, это системы в которых имеется
- 17. Характеристики и модели элементов и систем Статической характеристикой элемента называется зависимость установившихся значений выходной величины от
- 18. Характеристики и модели элементов и систем Астатическим называется элемент, у которого при постоянном входном воздействии сигнал
- 19. Характеристики и модели элементов и систем САР называется статической, если при постоянном входном воздействии ошибка управления
- 20. Динамические характеристики Переходной характеристикой h(t) называется реакция объекта на единичное ступенчатое воздействие при нулевых начальных условиях,
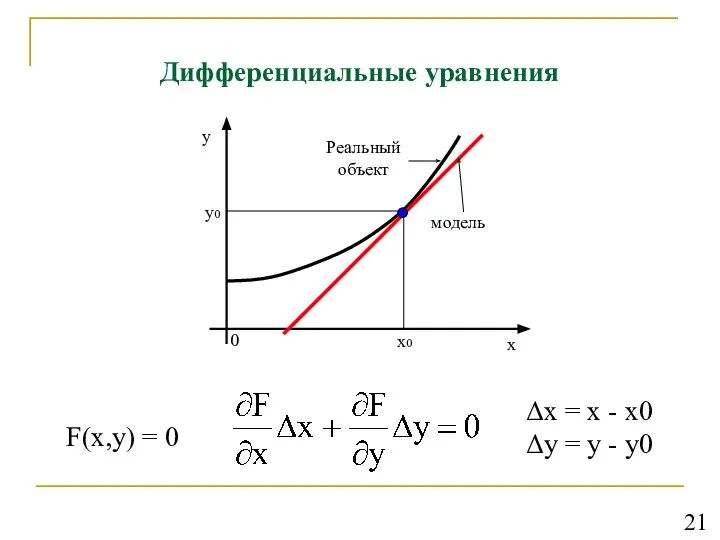
- 21. Дифференциальные уравнения Любые процессы передачи, обмена, преобразования энергии и вещества математически можно описать в виде дифференциальных
- 22. Дифференциальные уравнения Δх = х - х0 Δу = у - у0 F(х,у) = 0 21
- 23. Преобразования Лапласа Прямое преобразование Лапласа Обратное преобразование Лапласа 22
- 24. Передаточные функции Передаточной функцией называется отношение изображения выходного воздействия Y(s) к изображению входного X(s) при нулевых
- 25. Типовые звенья САР - усилительное Передаточная функция - идеально интегрирующее Передаточная функция Выходная величина Выходная величина
- 26. Типовые звенья САР - реальное интегрирующее Передаточная функция - идеально дифференцирующее Передаточная функция Выходная величина 25
- 27. Типовые звенья САР - реальное дифференцирующее Передаточная функция - апериодическое Передаточная функция Дифференциальное уравнение 26
- 28. Типовые звенья САР - колебательное Передаточная функция - запаздывающее Передаточная функция Дифференциальное уравнение Выходная величина 27
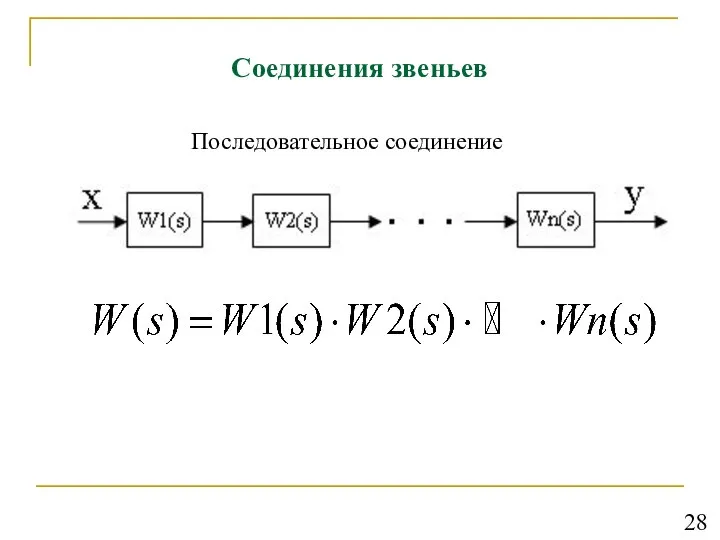
- 29. Соединения звеньев Последовательное соединение 28
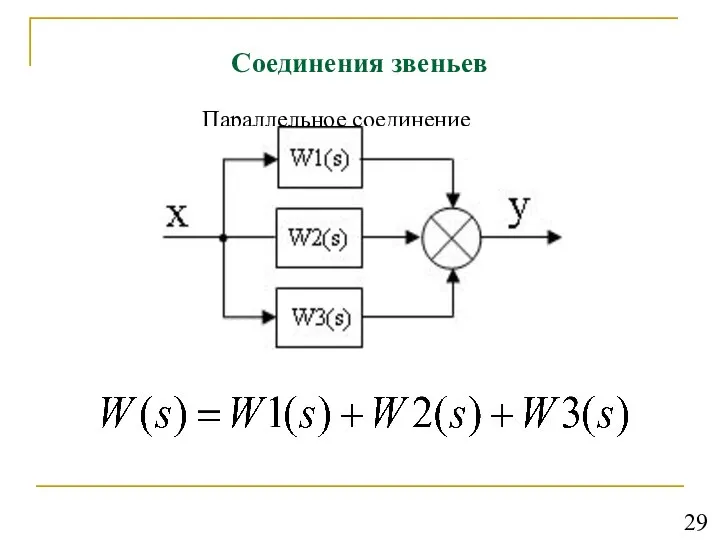
- 30. Соединения звеньев Параллельное соединение 29
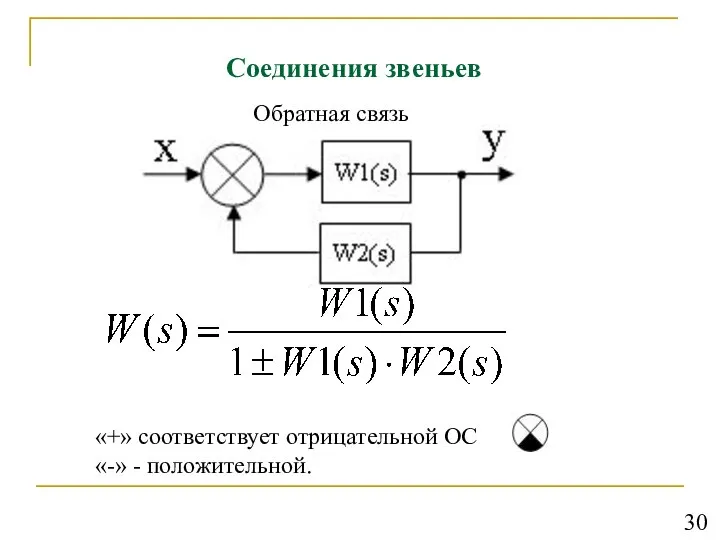
- 31. Соединения звеньев Обратная связь «+» соответствует отрицательной ОС «-» - положительной. 30
- 32. Передаточные функции САР 1) Для нахождения передаточной функции CAP в разомкнутом состоянии необходимо разомкнуть систему путем
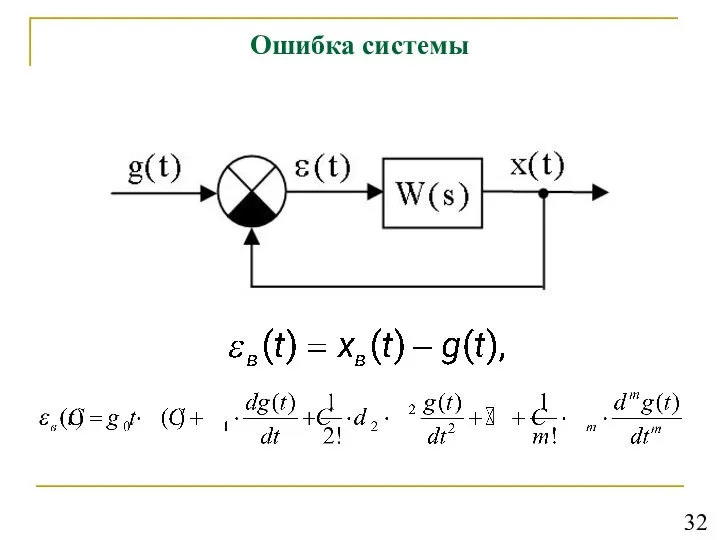
- 33. Ошибка системы 32
- 34. Коэффициенты ошибок 33
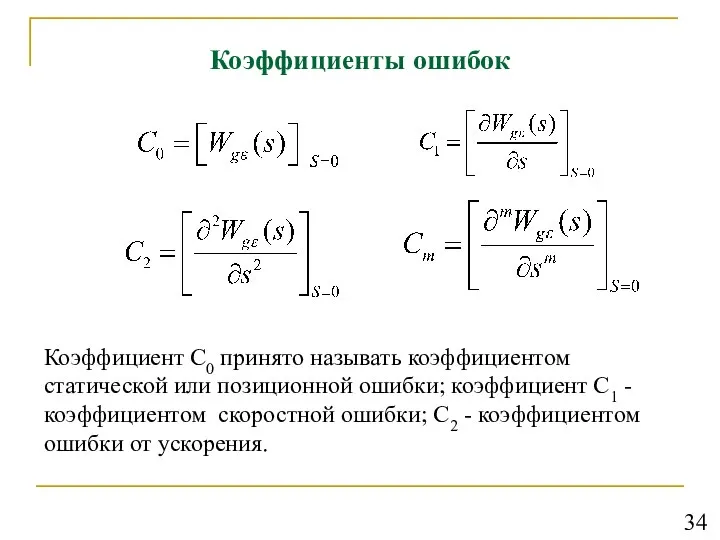
- 35. Коэффициенты ошибок Коэффициент С0 принято называть коэффициентом статической или позиционной ошибки; коэффициент С1 - коэффициентом скоростной
- 36. Коэффициенты ошибок 35
- 37. Критерий устойчивости Михайлова Характеристический полином 36
- 38. Критерий устойчивости Михайлова При изменении частоты ω вектор D(jω), изменяясь по величине и направлению, будет описывать
- 39. Критерий устойчивости Михайлова 38
- 40. Критерий устойчивости Михайлова Для того чтобы система автоматического управления была устойчива , необходимо и достаточно ,
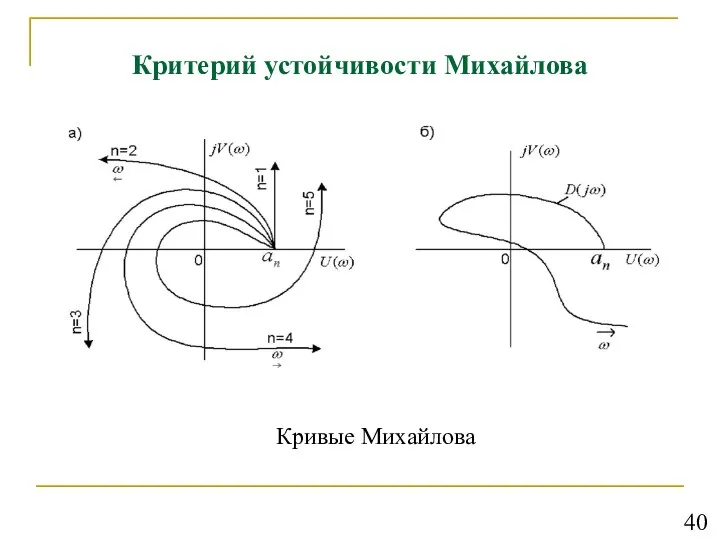
- 41. Критерий устойчивости Михайлова Кривые Михайлова 40
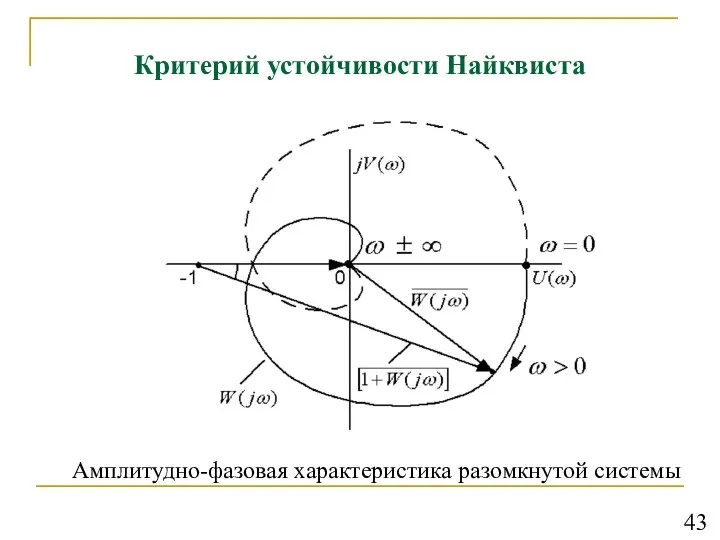
- 42. Критерий устойчивости Найквиста Критерий позволяет по амплитудно-фазовой частотной характеристике разомкнутой системы W(j ω) судить об устойчивости
- 43. Критерий устойчивости Найквиста Если k = 0 частотная характеристика не охватывает точку (-1,j0) , то система
- 44. Критерий устойчивости Найквиста Амплитудно-фазовая характеристика разомкнутой системы 43
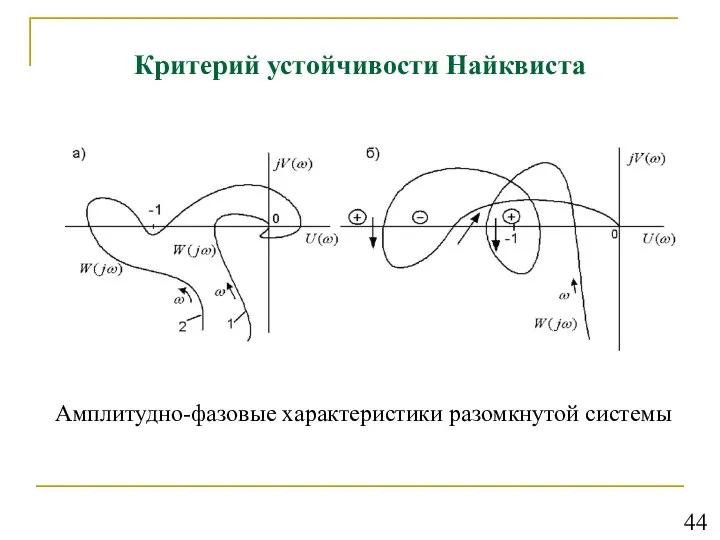
- 45. Критерий устойчивости Найквиста Амплитудно-фазовые характеристики разомкнутой системы 44
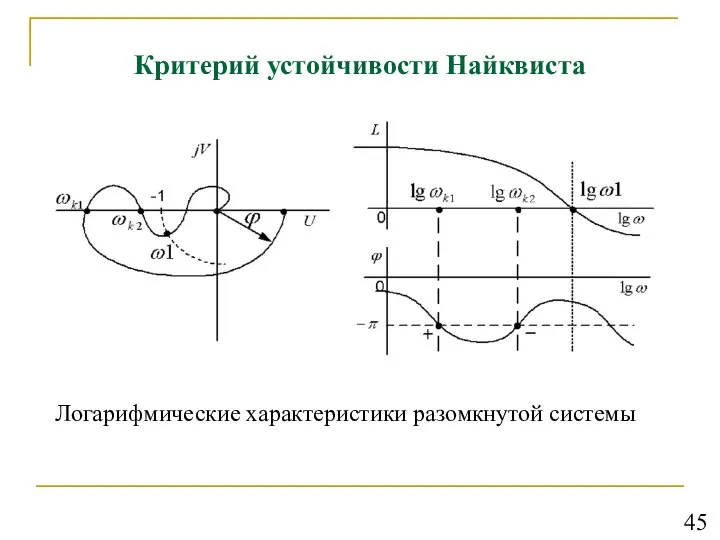
- 46. Критерий устойчивости Найквиста Логарифмические характеристики разомкнутой системы 45
- 47. Критерий устойчивости Гурвица Для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры
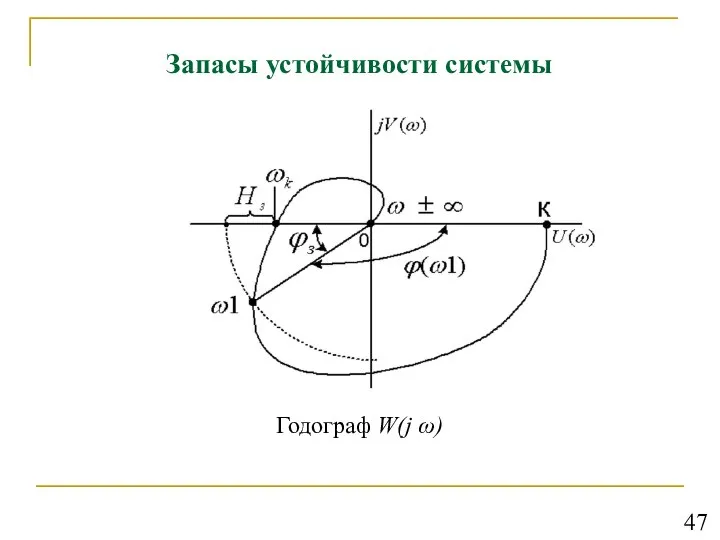
- 48. Запасы устойчивости системы Годограф W(j ω) 47
- 49. Показатели качества 1) прямые - определяемые непосредственно по кривой переходного процесса, 2) корневые - определяемые по
- 50. Оценки качества переходной характеристики Формула Хевисайда Перерегулирование 49
- 51. Оценки качества переходной характеристики Формула Хевисайда Перерегулирование 50
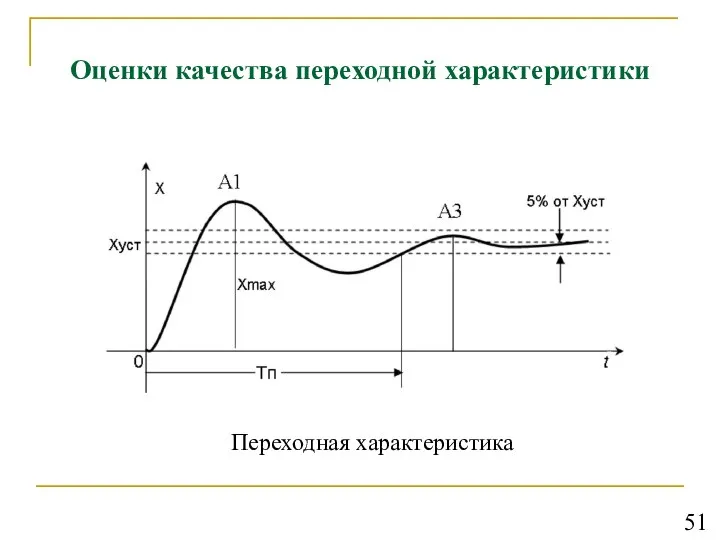
- 52. Оценки качества переходной характеристики Переходная характеристика 51
- 53. Оценки качества переходной характеристики Степень затухания Статическая ошибка εст = х - xуст Время регулирования (время
- 54. Корневые показатели качества Степень устойчивости Степень колебательности 53
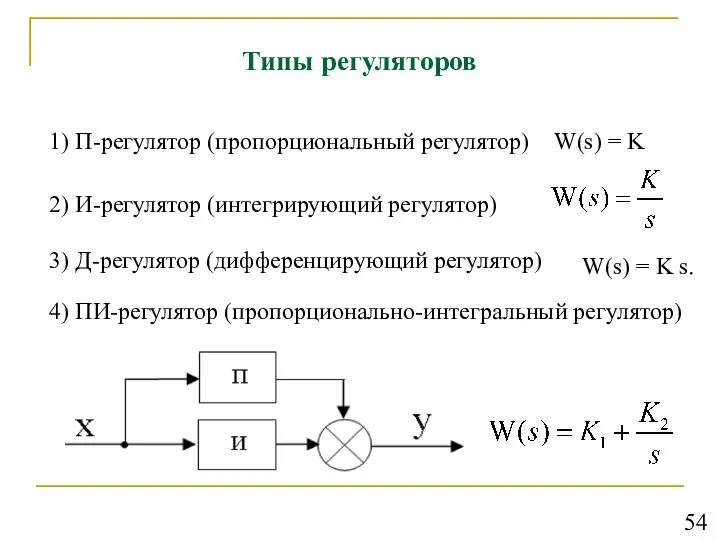
- 55. Типы регуляторов 1) П-регулятор (пропорциональный регулятор) W(s) = K 2) И-регулятор (интегрирующий регулятор) 3) Д-регулятор (дифференцирующий
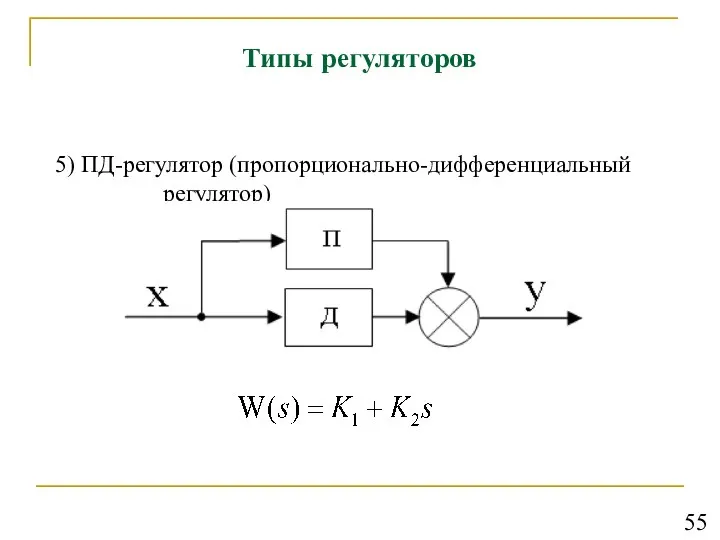
- 56. Типы регуляторов 5) ПД-регулятор (пропорционально-дифференциальный регулятор) 55
- 58. Скачать презентацию








































 Определение удельной плотности и температуры растворов
Определение удельной плотности и температуры растворов Условие равновесия рычага
Условие равновесия рычага 8 кл 3-4 Вн энергия. виды теплопередачи
8 кл 3-4 Вн энергия. виды теплопередачи Снежные причуды. Всё о снеге и снежинках
Снежные причуды. Всё о снеге и снежинках Презентация на тему Архимедова сила и ее значение в жизни человека
Презентация на тему Архимедова сила и ее значение в жизни человека  Электромагнитные колебания и волны
Электромагнитные колебания и волны Презентация на тему Первый закон термодинамики
Презентация на тему Первый закон термодинамики  Вес тела. Невесомость
Вес тела. Невесомость Сдвиг. Срез. Смятие
Сдвиг. Срез. Смятие Презентация по физике "Внутреннее устройство разных типов двигателей" -
Презентация по физике "Внутреннее устройство разных типов двигателей" -  Квантовые свойства микрочастиц. Волны де Бройля. Волновая функция
Квантовые свойства микрочастиц. Волны де Бройля. Волновая функция Электростатика. Электродинамика
Электростатика. Электродинамика Презентация на тему газовые законы
Презентация на тему газовые законы  Презентация на тему Электрическое поле (10 класс)
Презентация на тему Электрическое поле (10 класс)  Методы повышения конструкционной прочности деталей машин
Методы повышения конструкционной прочности деталей машин Соединение конденсаторов
Соединение конденсаторов Швидкість реакції між металом або сплавом з реакційним газом
Швидкість реакції між металом або сплавом з реакційним газом Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей
Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей Расчет средней энергии нормальных колебаний кристаллической решетки
Расчет средней энергии нормальных колебаний кристаллической решетки Примеры расчета индукции магнитного поля
Примеры расчета индукции магнитного поля Нанотехнологии, как приобретенное направление развития науки в РФ
Нанотехнологии, как приобретенное направление развития науки в РФ Исследование электронных свойств переходных металлов методами ОЭС и РФЭС. Атомоподобные оже-спектры
Исследование электронных свойств переходных металлов методами ОЭС и РФЭС. Атомоподобные оже-спектры Оптоволоконные лазеры
Оптоволоконные лазеры Закон сохранения энергии, работа и мощность в механике
Закон сохранения энергии, работа и мощность в механике Электромагнитное поле. Викторина
Электромагнитное поле. Викторина Поглощенная доза излучения. Основы дозиметрии
Поглощенная доза излучения. Основы дозиметрии Механическая работа и мощность
Механическая работа и мощность Презентация на тему Тепловые явления
Презентация на тему Тепловые явления