Содержание
- 2. Введение “Всякий человек, знакомый с механикой, знает закон Д’Аламбера, понимает его значение и с уважением произносит
- 3. Д’Аламбер, Жан Лерон 2
- 4. Родители Клодина Герен де Тансен Филипп Детуш 3
- 5. Колледж имени Мазарини 4
- 6. Трактат о динамике 5 Принцип инерции Принцип сложения движения Принцип равновесия Принцип Даламбера
- 7. Принцип Д’Аламбера для точки Пусть на материальную точку массой m действуют активные силы с их равнодействующей
- 8. Принцип Д’Аламбера для системы тел Для каждой точки системы: 7 Сложив уравнения всех точек системы почленно,
- 9. Энциклопедия, или Толковый словарь наук, искусств и ремёсел 8
- 10. Жюли де Леспинас 9
- 11. 10 Кратер Д’Аламбер (лат. d'Alembert) — громадный ударный кратер в северном полушарии обратной стороны Луны. Название
- 12. 11
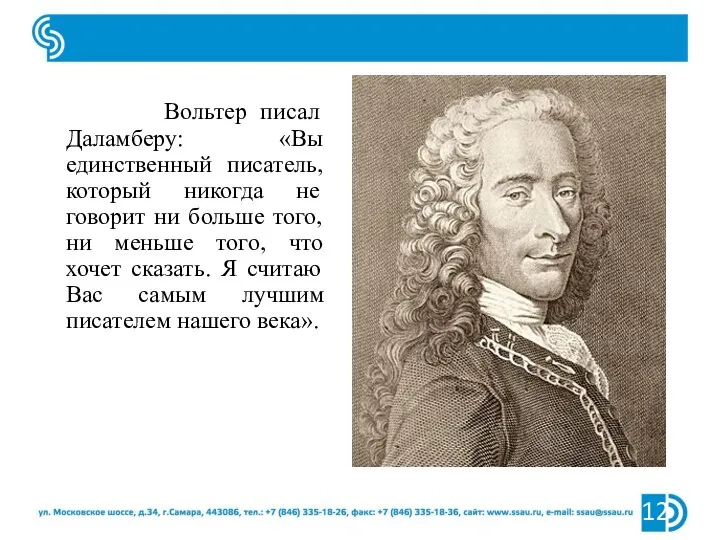
- 13. Вольтер писал Даламберу: «Вы единственный писатель, который никогда не говорит ни больше того, ни меньше того,
- 14. «Да, математика — это моя самая старая любовь, самая верная возлюбленная!» Статуя Д’Аламбера в Лувре 13
- 16. Скачать презентацию












 Что значит минута
Что значит минута Электростатика. Электрические взаимодействия
Электростатика. Электрические взаимодействия Виды излучений. Источники света
Виды излучений. Источники света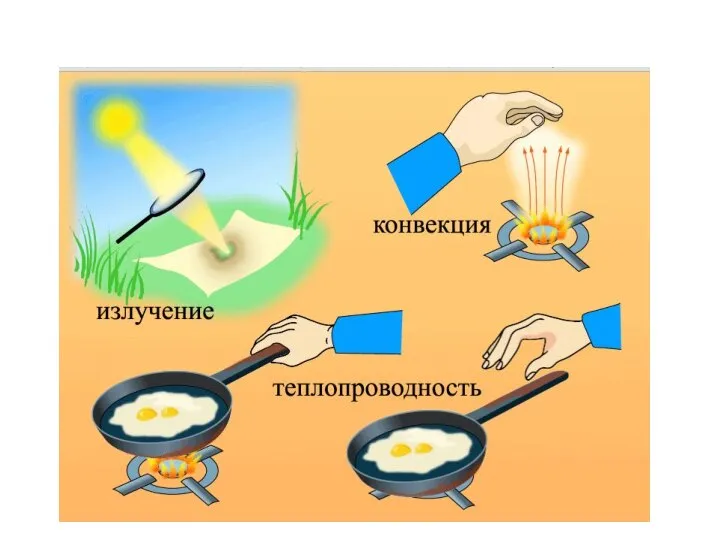 Молекулярная физика
Молекулярная физика Термодинамика фазовых равновесий. Правило фаз Гиббса
Термодинамика фазовых равновесий. Правило фаз Гиббса Презентация на тему Изменение агрегатного состояния вещества
Презентация на тему Изменение агрегатного состояния вещества  Интерпретация спектральной классификации. (Тема 18)
Интерпретация спектральной классификации. (Тема 18) Работа газа и пара при расширении. Двигатель внутреннего сгорания
Работа газа и пара при расширении. Двигатель внутреннего сгорания ВКР: Пороговые значения достаточной статистики. Задачи обнаружения сигнала со случайной начальной фазой
ВКР: Пороговые значения достаточной статистики. Задачи обнаружения сигнала со случайной начальной фазой Переменный ток
Переменный ток Задачи небесной механики
Задачи небесной механики Архимед көче
Архимед көче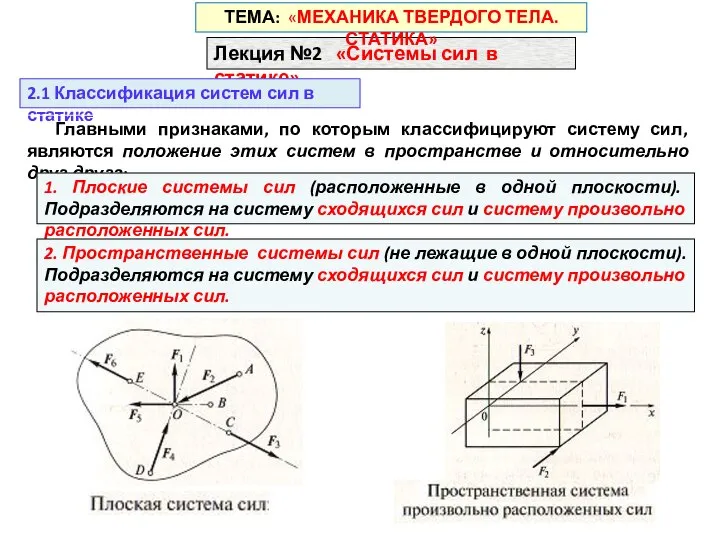 Системы сил в статике
Системы сил в статике Электрический двигатель постоянного тока. Лабораторная работа
Электрический двигатель постоянного тока. Лабораторная работа Энергия магнитного поля
Энергия магнитного поля Сложение сил. Равнодействующая сил
Сложение сил. Равнодействующая сил Потребление и экономия электрической энергии в школе и дома
Потребление и экономия электрической энергии в школе и дома Медицинское открытие. Бионические контактные линзы
Медицинское открытие. Бионические контактные линзы Сложение потенциальных потоков
Сложение потенциальных потоков Единая система допусков и посадок деталей и узлов машин, принципы её построения
Единая система допусков и посадок деталей и узлов машин, принципы её построения Электричество и магнетизм
Электричество и магнетизм Агрегатные состояния вещества
Агрегатные состояния вещества Строение атома
Строение атома Расчет стержневых конструкций по предельному равновесию
Расчет стержневых конструкций по предельному равновесию Количество теплоты, обобщающий урок-практикум, 8, 10 класс
Количество теплоты, обобщающий урок-практикум, 8, 10 класс Методы диагностирования автотранспортных средств
Методы диагностирования автотранспортных средств Теплоёмкость газа
Теплоёмкость газа Состав и характеристика атомного ядра
Состав и характеристика атомного ядра