Дифракция света

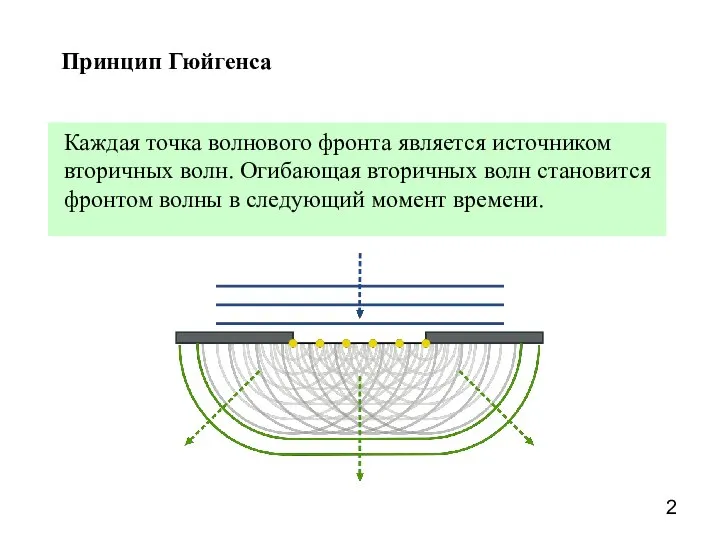
Принцип Гюйгенса
Каждая точка волнового фронта является источником вторичных волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени.

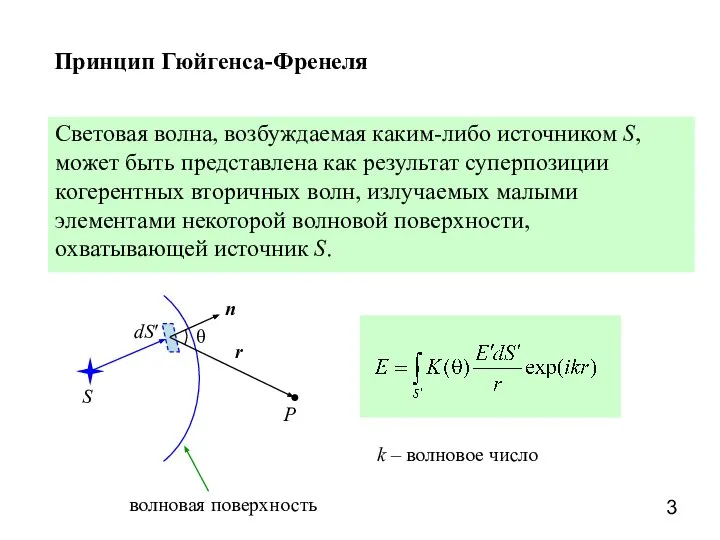
Принцип Гюйгенса-Френеля
Световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых малыми элементами некоторой волновой поверхности, охватывающей источник S.
S
dS′
n
r
θ
P
k – волновое число
волновая поверхность

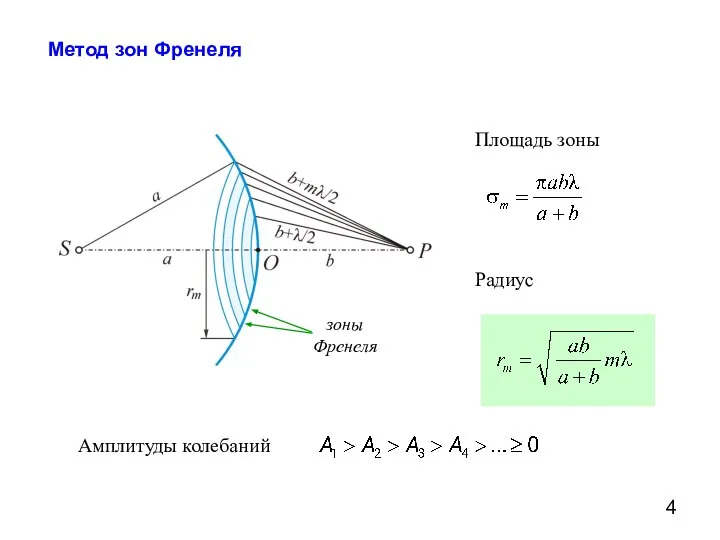
Метод зон Френеля
зоны
Френеля
Площадь зоны
Радиус
Амплитуды колебаний

Колебания, приходящие в точку P от двух соседних зон, находятся в противофазе. Поэтому
Амплитуда Am убывает очень медленно и поэтому можно считать
После перегруппировки

Метод векторных диаграмм
Каждая зона разбивается на серию узких кольцевых подзон. Колебание, создаваемое каждой подзоной в точке P, изображается на диаграмме в виде маленькой стрелочки. Стрелочки повернуты друг относительно друга на угол Δφ, соответствующий сдвигу фаз колебаний.
Каждая следующая стрелочка чуть короче предыдущей.
действие 1-й зоны
действие 2-х зон
действие 3-х зон

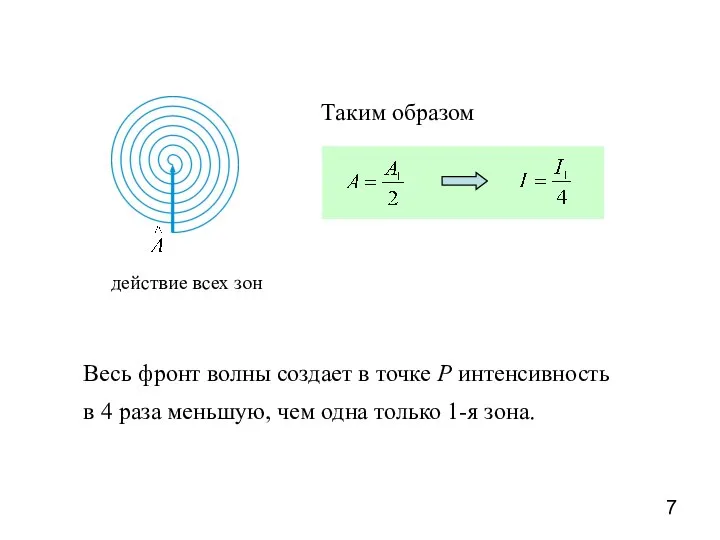
действие всех зон
Таким образом
Весь фронт волны создает в точке Р интенсивность в 4 раза меньшую, чем одна только 1-я зона.

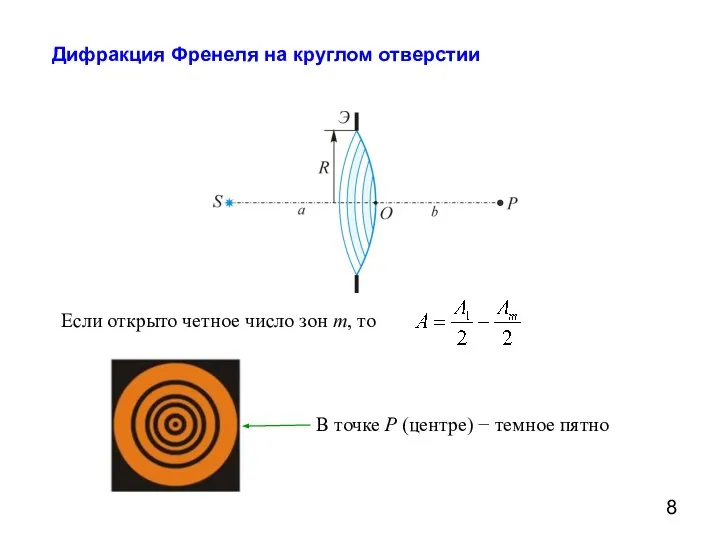
Дифракция Френеля на круглом отверстии
Если открыто четное число зон m, то
В точке P (центре) − темное пятно

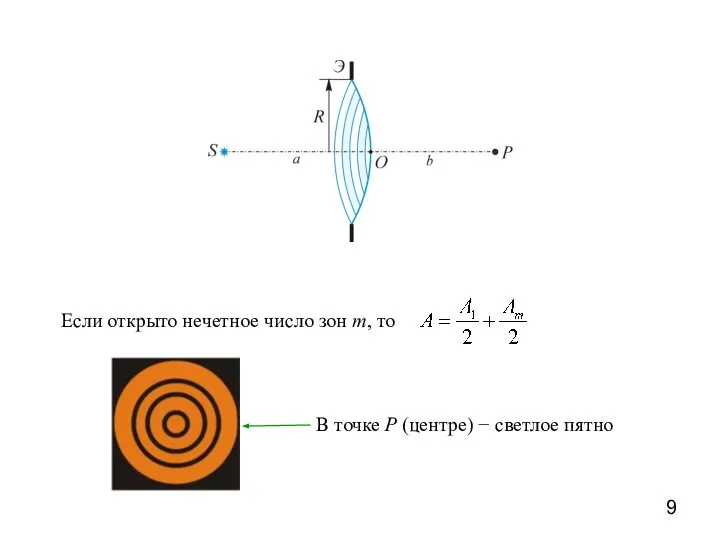
Если открыто нечетное число зон m, то
В точке P (центре) − светлое пятно

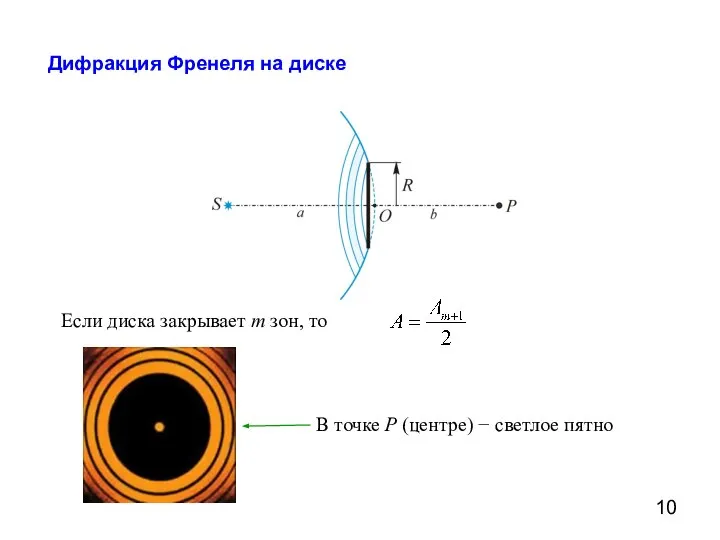
Дифракция Френеля на диске
Если диска закрывает m зон, то
В точке P (центре) − светлое пятно

Зонная пластинка
Зонные пластинки Френеля. Слева − открыты нечетные зоны, справа − чётные.
Если на пути световых волн поставить такую пластинку, то интенсивность света в точке P резко возрастает. Амплитуда в этой точке будет равна сумме амплитуд от нечетных (или четных) зон. Соответственно интенсивность I = 4n2I0, где I0 − интенсивность при свободном распространении света, n − число открытых зон.
Пластинка подобна линзе:

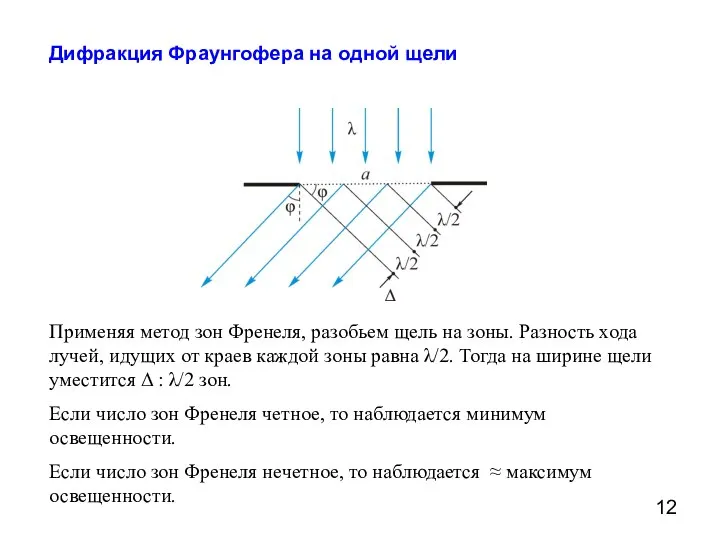
Дифракция Фраунгофера на одной щели
Применяя метод зон Френеля, разобьем щель на зоны. Разность хода лучей, идущих от краев каждой зоны равна λ/2. Тогда на ширине щели уместится Δ : λ/2 зон.
Если число зон Френеля четное, то наблюдается минимум освещенности.
Если число зон Френеля нечетное, то наблюдается ≈ максимум освещенности.

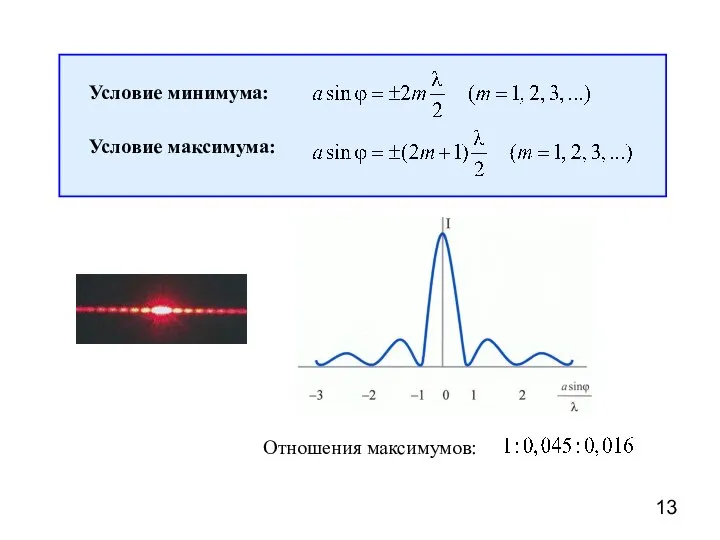
Условие минимума:
Условие максимума:
Отношения максимумов:

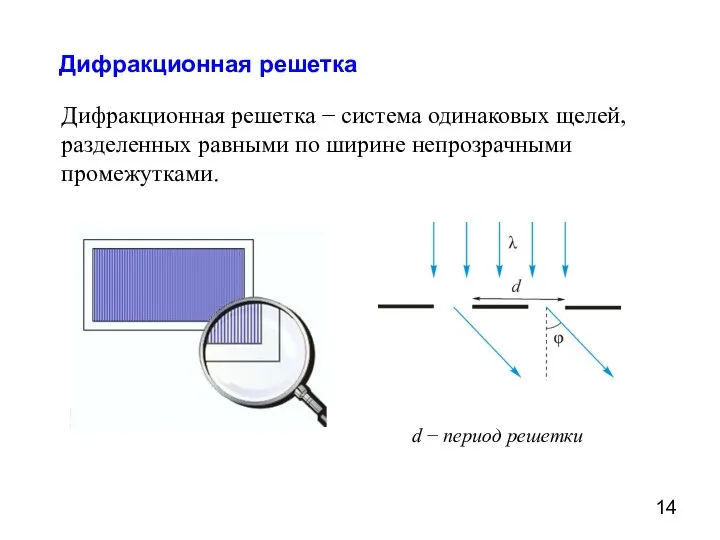
Дифракционная решетка
Дифракционная решетка − система одинаковых щелей, разделенных равными по ширине непрозрачными промежутками.
d − период решетки

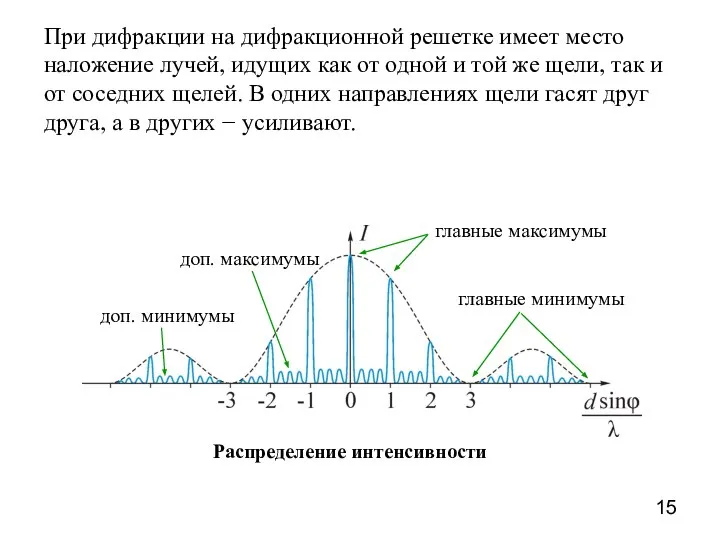
При дифракции на дифракционной решетке имеет место наложение лучей, идущих как от одной и той же щели, так и от соседних щелей. В одних направлениях щели гасят друг друга, а в других − усиливают.
Распределение интенсивности
главные максимумы
главные минимумы
доп. максимумы
доп. минимумы

Условие главных максимумов
m − порядок главного максимума
Для данных направлений колебания от отдельных щелей взаимно усиливают друг друга. Интенсивность главного максимума в N2 раз превосходит интенсивность от щели в этом же направлении. N − число щелей.
Наибольший порядок главного максимума

Условие главных минимумов
a − ширина щели
В данных направлениях интенсивность, создаваемая каждой из щелей в отдельности, равна нулю, поэтому и результирующая интенсивность в этих направлениях будет также равна нулю.

Условие дополнительных минимумов
N − число щелей
Между соседними главными максимумами имеется N−1 дополнительный минимум. В данных направлениях колебания от отдельных щелей взаимно погашают друг друга.
Между дополнительными минимумами располагаются N−2 слабых дополнительных максимумов. Интенсивность этих максимумов не превышает 1/22 интенсивности ближайшего главного максимума.

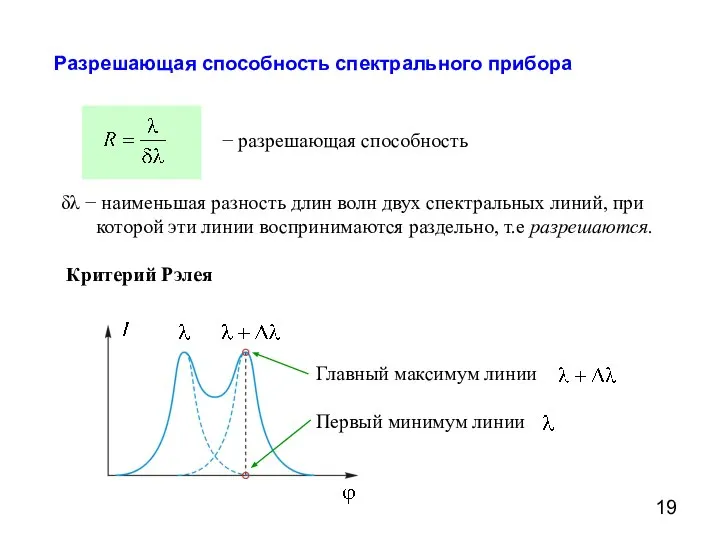
Разрешающая способность спектрального прибора
δλ − наименьшая разность длин волн двух спектральных линий, при
которой эти линии воспринимаются раздельно, т.е разрешаются.
Критерий Рэлея
Главный максимум линии
Первый минимум линии
− разрешающая способность

Две спектральные линии с равными интенсивностями разрешены, если главный максимум одной линии совпадает с первым минимумом другой.
Отсюда, разрешающая способность дифракционной решетки

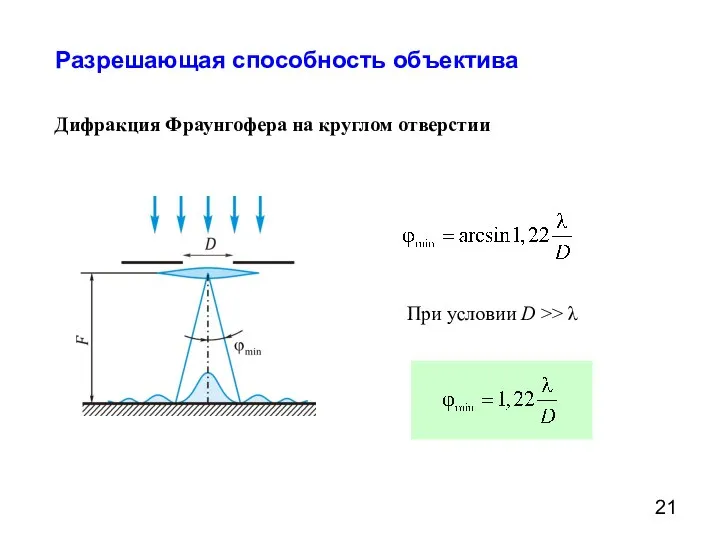
Разрешающая способность объектива
Дифракция Фраунгофера на круглом отверстии
При условии D >> λ

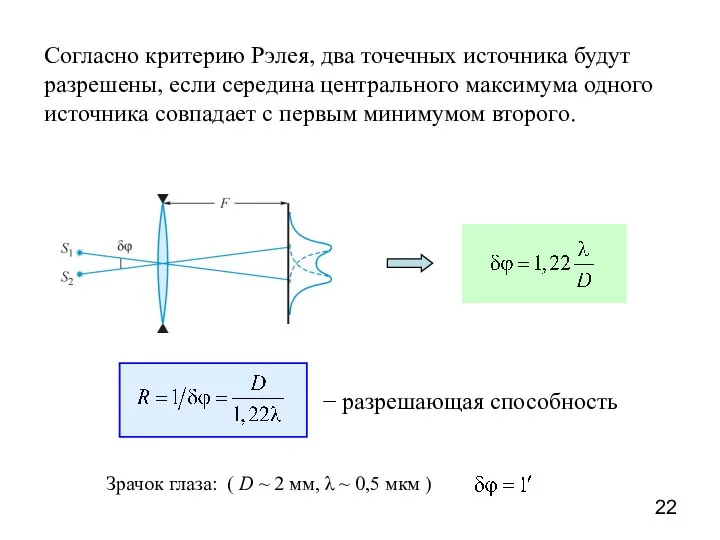
Согласно критерию Рэлея, два точечных источника будут разрешены, если середина центрального максимума одного источника совпадает с первым минимумом второго.
− разрешающая способность
Зрачок глаза: ( D ~ 2 мм, λ ~ 0,5 мкм )

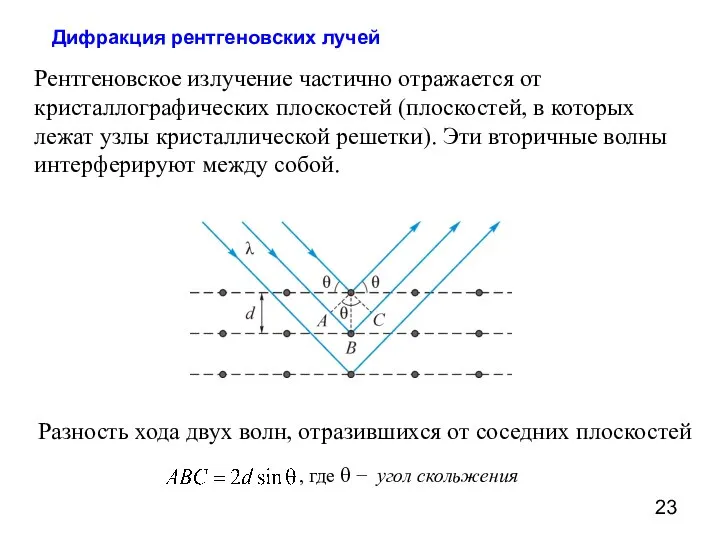
Дифракция рентгеновских лучей
Рентгеновское излучение частично отражается от кристаллографических плоскостей (плоскостей, в которых лежат узлы кристаллической решетки). Эти вторичные волны интерферируют между собой.
Разность хода двух волн, отразившихся от соседних плоскостей
, где θ − угол скольжения

Дифракционные максимумы:
− формула Вульфа-Брегга
Применение рентгеновской дифракции:
1) Рентгеноструктурный анализ
По известным λ и θ находят межплоскостные расстояния и определяют кристаллическую структуру.
2) Рентгеновская спектроскопия
По известным d и θ находят длину волны рентгеновского
излучения.