Содержание
- 2. От динамики Аристотеля к динамике Ньютона Аристотель, 384-322 г. до н.э. Николай Кузанский 1401-1464 Аристотель: каждому
- 3. Динамика как раздел механики При движении тела его скорость может изменяться по модулю и направлению движение
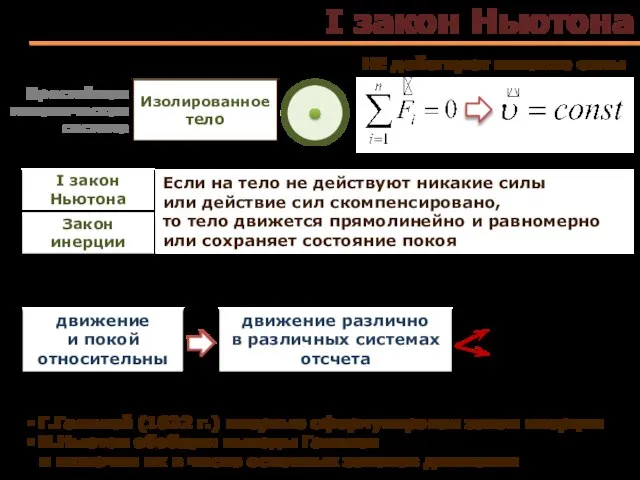
- 4. I закон Ньютона Простейшая механическая система Изолированное тело НЕ действуют никакие силы Если на тело не
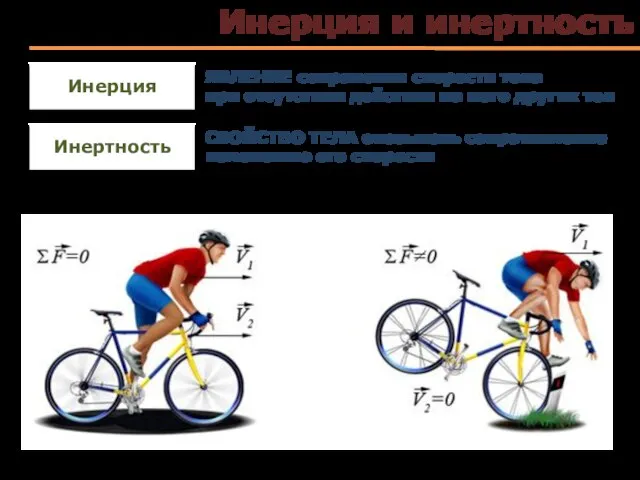
- 5. Инерция и инертность Инерция ЯВЛЕНИЕ сохранения скорости тела при отсутствии действия на него других тел Инертность
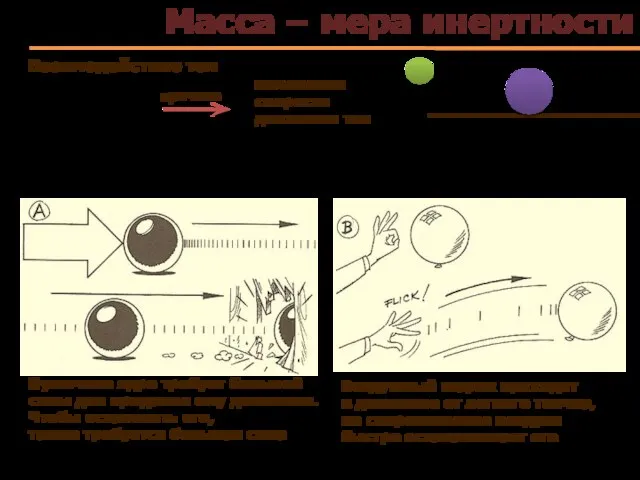
- 6. Масса в классической механике Инертная масса тела Количественная мера инертности тела Скалярная физическая величина, характеризующая способность
- 7. Масса – мера инертности изменения скорости движения тел Взаимодействие тел причина Пушечное ядро требует большой силы
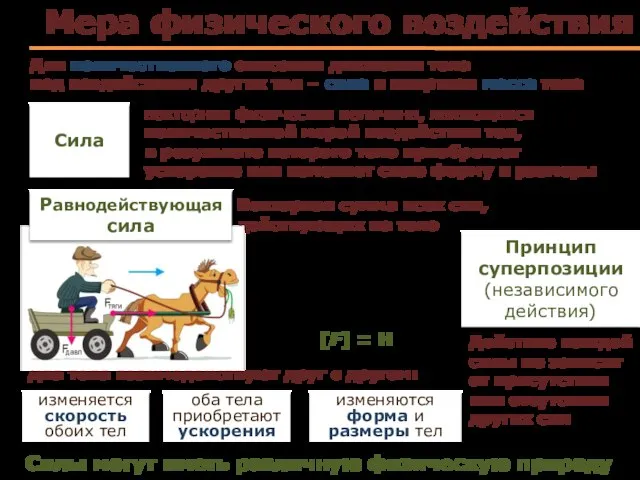
- 8. оба тела приобретают ускорения изменяется скорость обоих тел Мера физического воздействия Для количественного описания движения тела
- 9. Сила F характеризуется: численным значением направлением в пространстве точкой приложения Сила
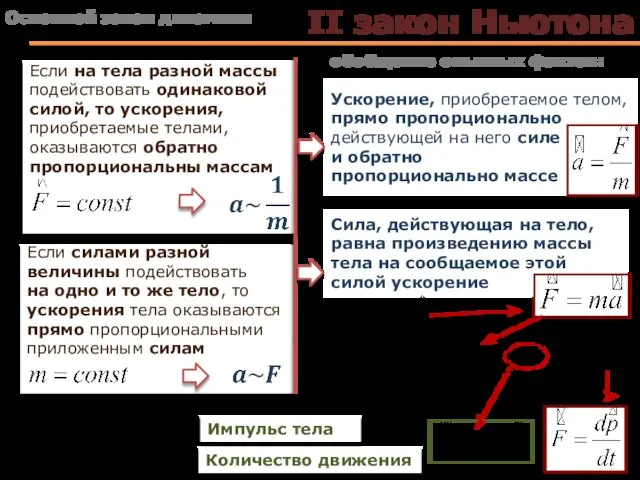
- 10. Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам
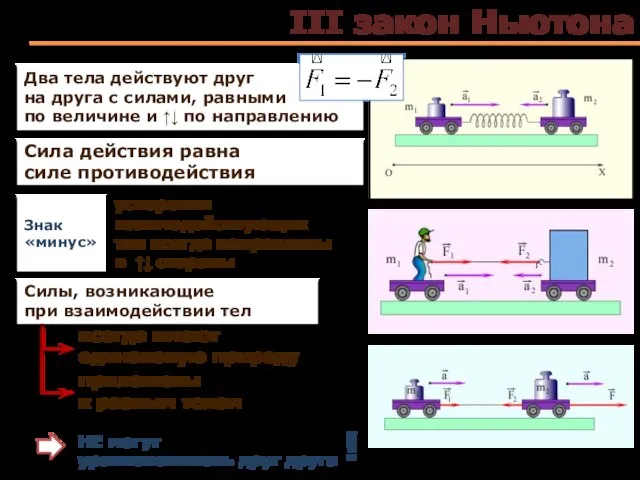
- 11. III закон Ньютона Два тела действуют друг на друга с силами, равными по величине и ↑↓
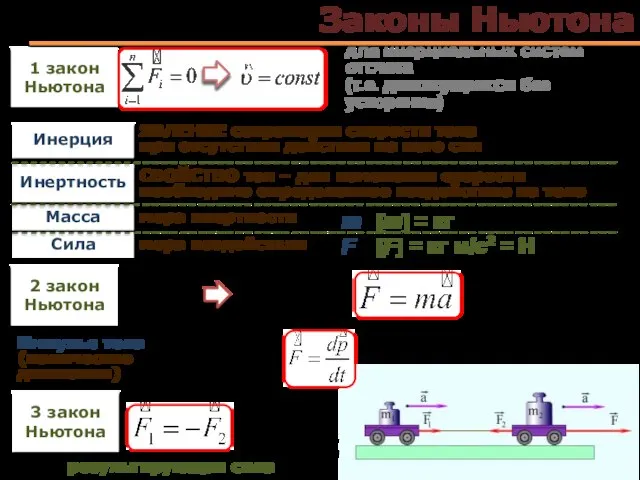
- 12. Законы Ньютона 1 закон Ньютона для инерциальных систем отсчета (т.е. движущихся без ускорения) 2 закон Ньютона
- 13. Инерциальные системы отсчета В механике Ньютона законы взаимодействия тел формулируются для класса ИСО Инерциальные системы отсчета
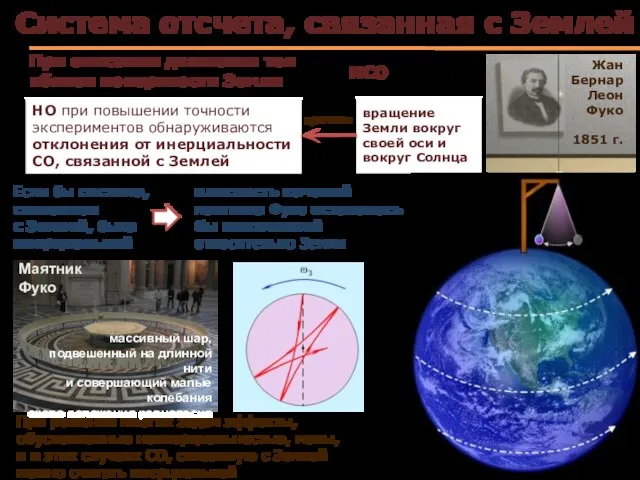
- 14. Система отсчета, связанная с Землей НО при повышении точности экспериментов обнаруживаются отклонения от инерциальности СО, связанной
- 15. гелиоцентрическая (звездная) система отсчета: начало координат – в центре Солнца, оси проведены в направлении определенных звезд
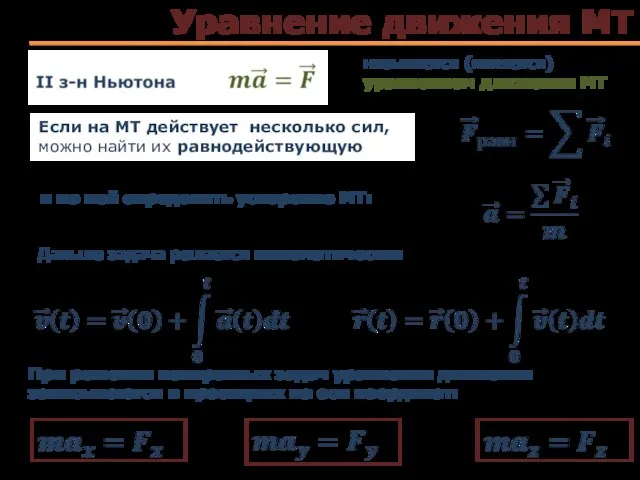
- 16. Уравнение движения МТ называется (является) уравнением движения МТ Если на МТ действует несколько сил, можно найти
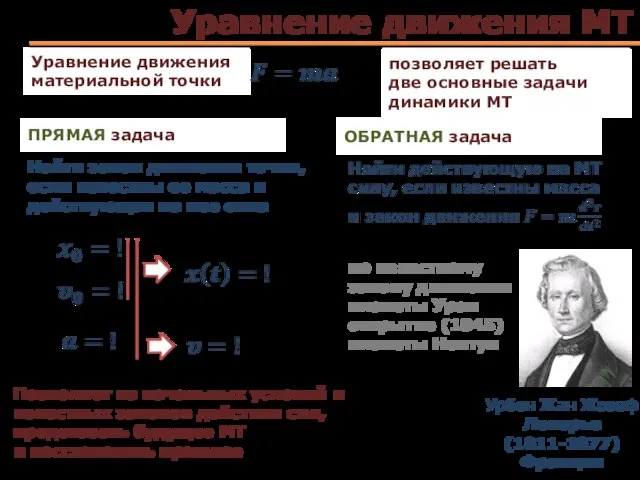
- 17. Уравнение движения МТ Уравнение движения материальной точки позволяет решать две основные задачи динамики МТ ПРЯМАЯ задача
- 18. Преобразования Галилея Преобразования Галилея Законы Ньютона справедливы в инерциальных системах отсчета при скоростях, много меньших скорости
- 19. Принцип относительности Галилея Все механические явления в различных ИСО (инерциальных системах отсчета) подчиняются одним и тем
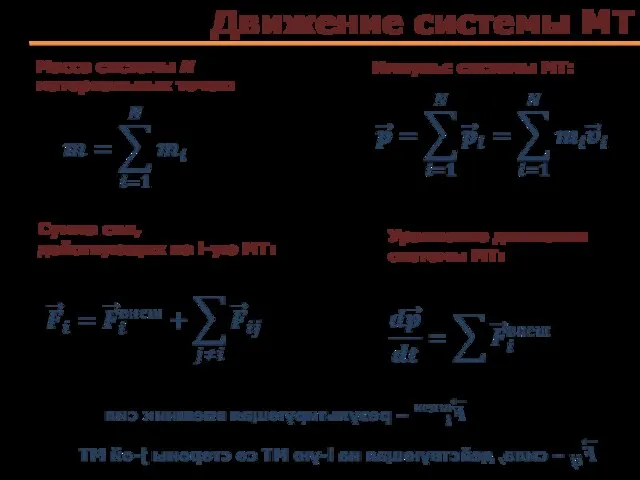
- 20. Движение системы МТ Масса системы N материальных точек: Импульс системы МТ: Сумма сил, действующих на i-ую
- 21. Центр масс системы МТ СКОРОСТЬ движения центра масс: ИМПУЛЬС системы МТ:
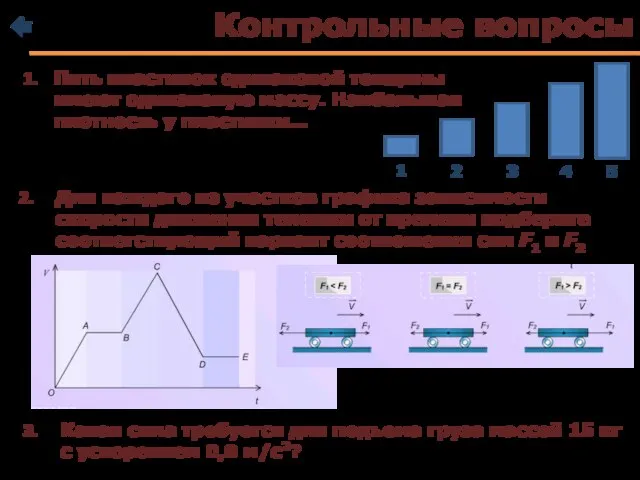
- 22. Контрольные вопросы Пять пластинок одинаковой толщины имеют одинаковую массу. Наибольшая плотность у пластинки… 1 2 3
- 23. Сильное Слабое Электромагнитное Гравитационное Определяет взаимодействие между кварками и определяет структуру ядер Действует на расстояниях r
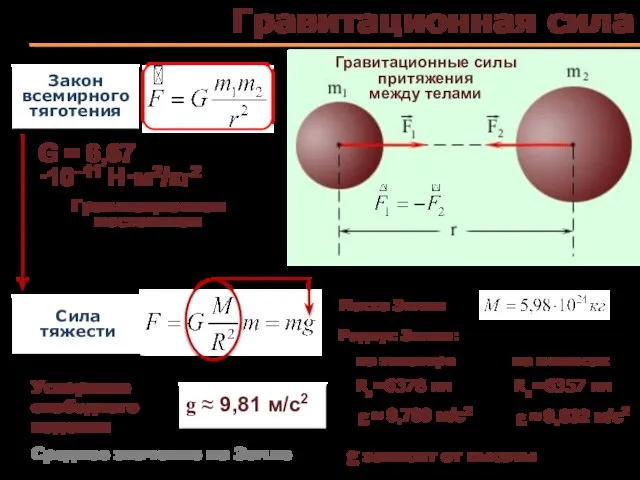
- 24. Гравитационная сила Закон всемирного тяготения Гравитационные силы притяжения между телами Сила тяжести G = 6,67·10–11 Н·м2/кг2
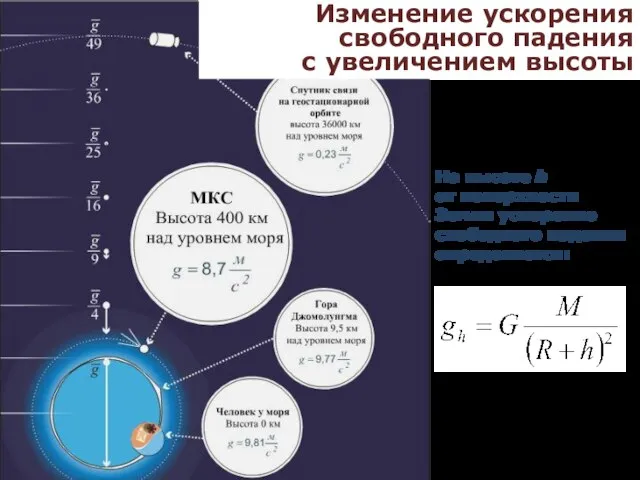
- 25. Изменение ускорения свободного падения с увеличением высоты На высоте h от поверхности Земли ускорение свободного падения
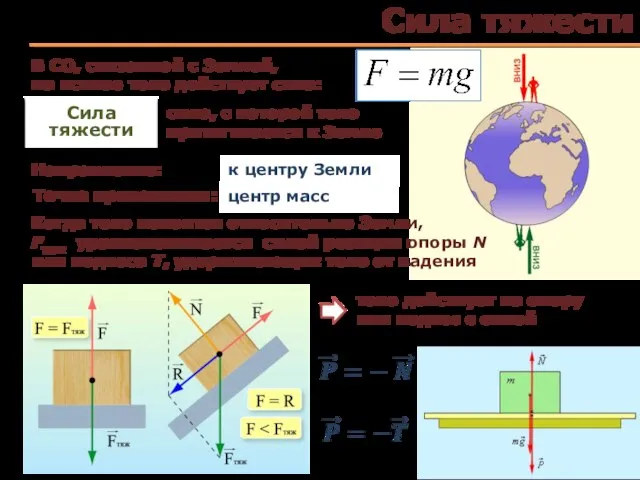
- 26. Сила тяжести Сила тяжести Направление: сила, с которой тело притягивается к Земле Точка приложения: ? ?
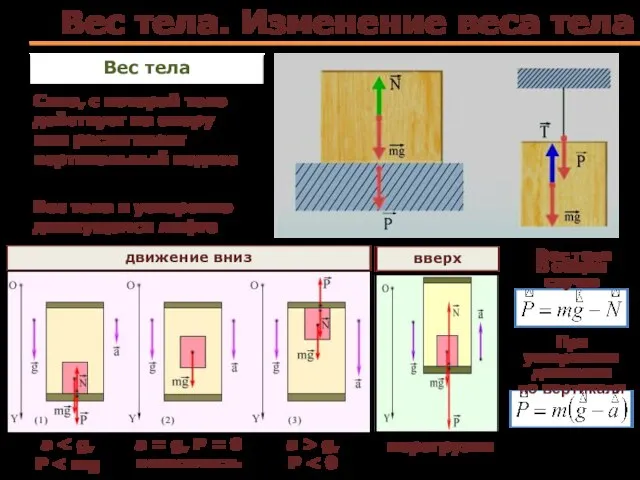
- 27. Вес тела. Изменение веса тела Вес тела Вес тела В общем случае При ускоренном движении по
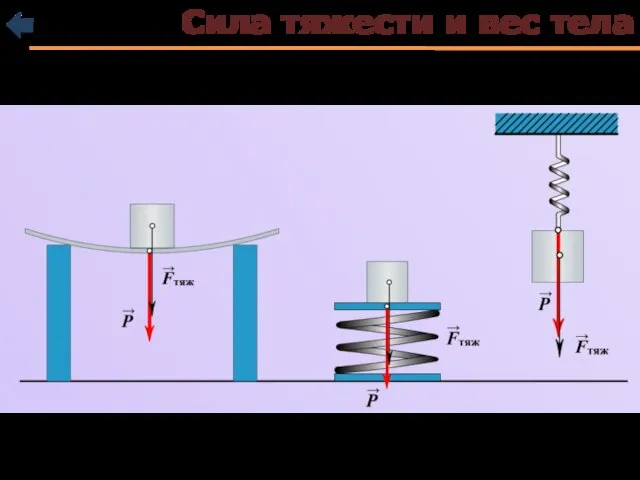
- 28. Сила тяжести и вес тела
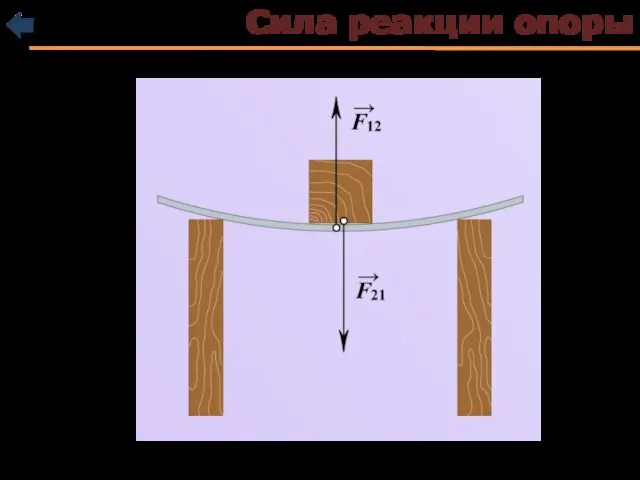
- 29. Сила реакции опоры
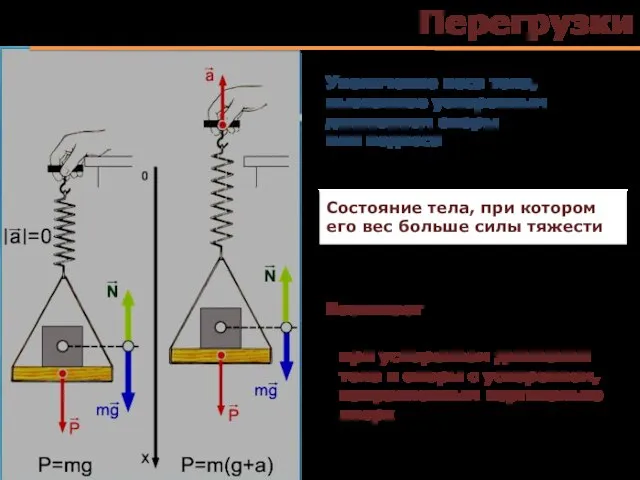
- 30. Перегрузки при ускоренном движении тела и опоры с ускорением, направленным вертикально вверх Увеличение веса тела, вызванное
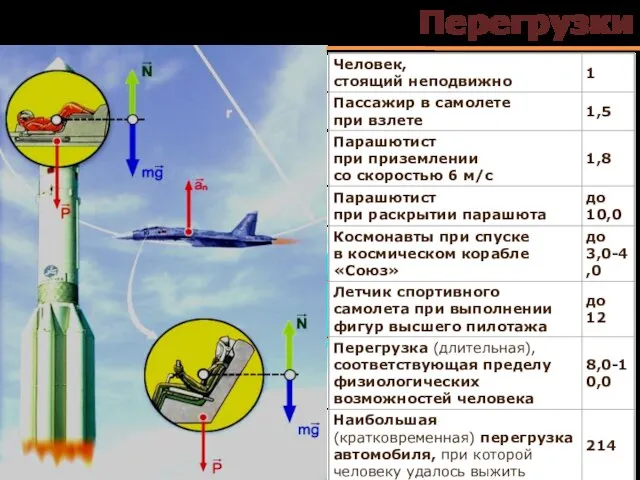
- 31. Перегрузки
- 32. Невесомость на Земле в невесомости
- 33. Упругие силы Под действием приложенных к нему сил всякое реальное тело ДЕФОРМИРУЕТСЯ, т.е. изменяет свои размеры
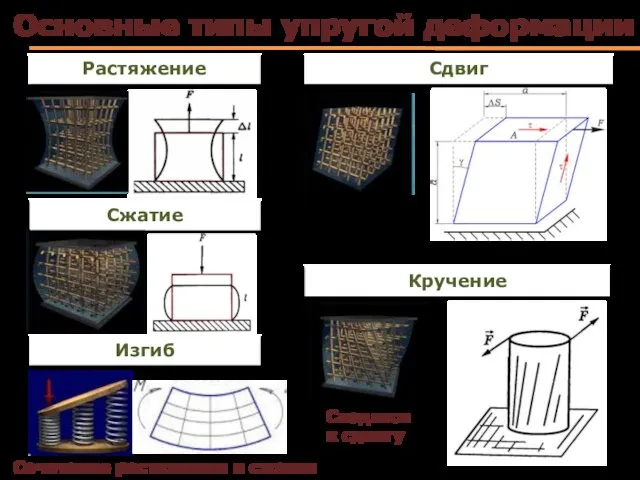
- 34. Основные типы упругой деформации Сдвиг Сводится к сдвигу Изгиб Сочетание растяжения и сжатия Растяжение Сжатие Кручение
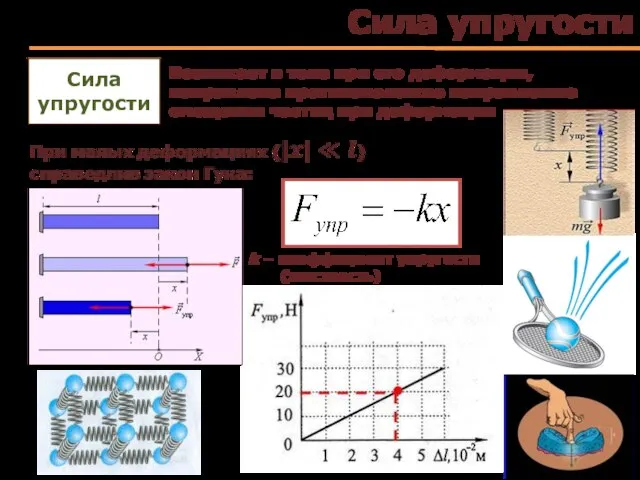
- 35. Сила упругости Сила упругости Возникает в теле при его деформации, направлена противоположно направлению смещения частиц при
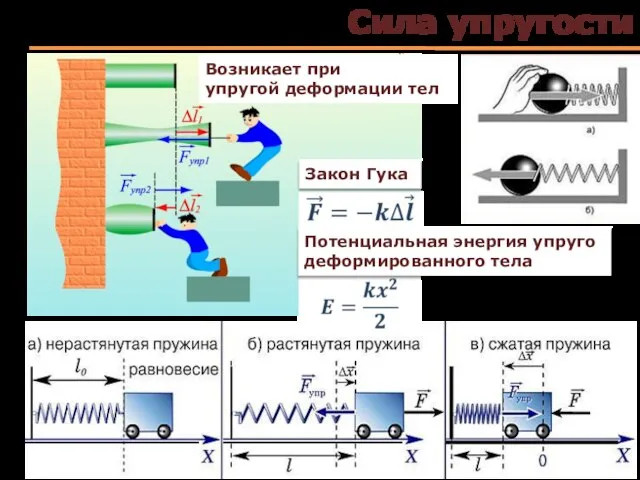
- 36. Сила упругости Возникает при упругой деформации тел Потенциальная энергия упруго деформированного тела Закон Гука
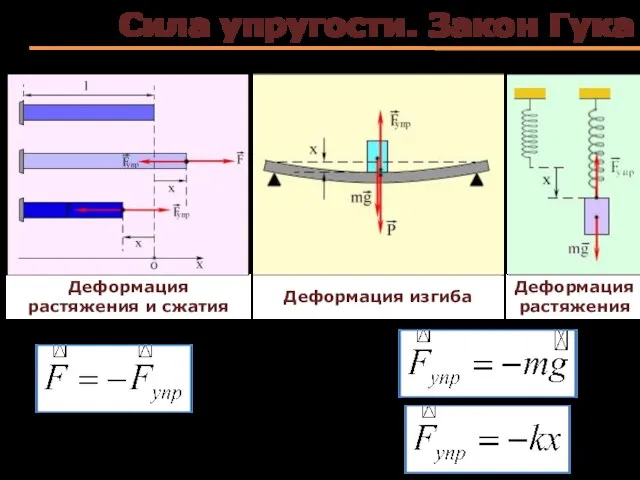
- 37. Сила упругости. Закон Гука Деформация изгиба Деформация растяжения Деформация растяжения и сжатия
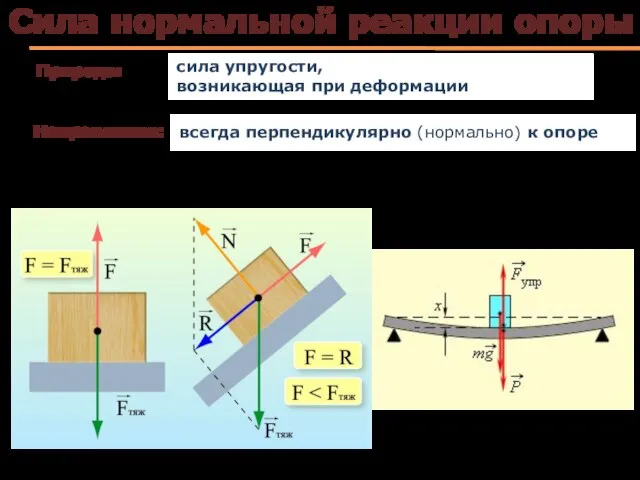
- 38. Сила нормальной реакции опоры Природа: сила упругости, возникающая при деформации Направление: всегда перпендикулярно (нормально) к опоре
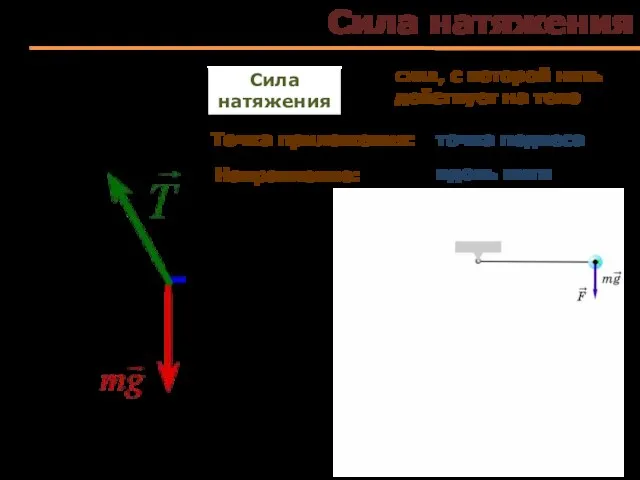
- 39. Сила натяжения сила, с которой нить действует на тело Точка приложения: Сила натяжения Направление: точка подвеса
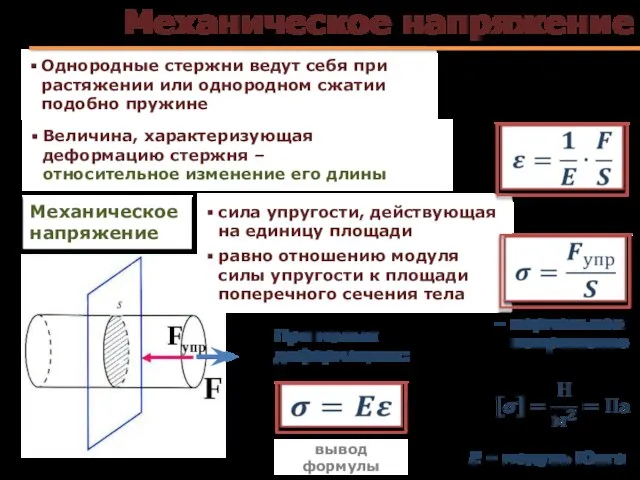
- 40. Механическое напряжение Однородные стержни ведут себя при растяжении или однородном сжатии подобно пружине Величина, характеризующая деформацию
- 42. Модуль Юнга Зависит только от свойств материала и НЕ зависит от размеров и формы тела Показывает
- 43. Батут
- 44. Катапульты
- 45. Лук
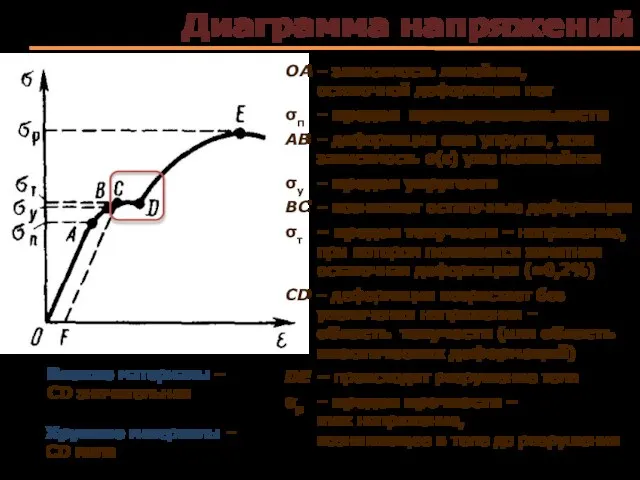
- 46. Диаграмма напряжений ОА – зависимость линейная, остаточной деформации нет σп – предел пропорциональности АВ – деформация
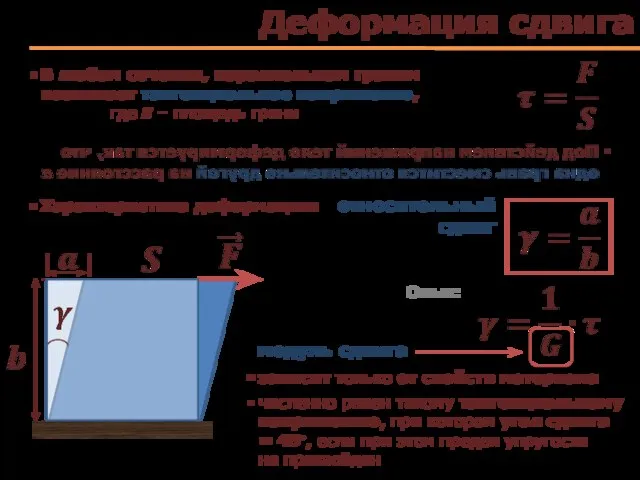
- 47. Деформация сдвига В любом сечении, параллельном граням возникает тангенциальное напряжение, где S – площадь грани Характеристика
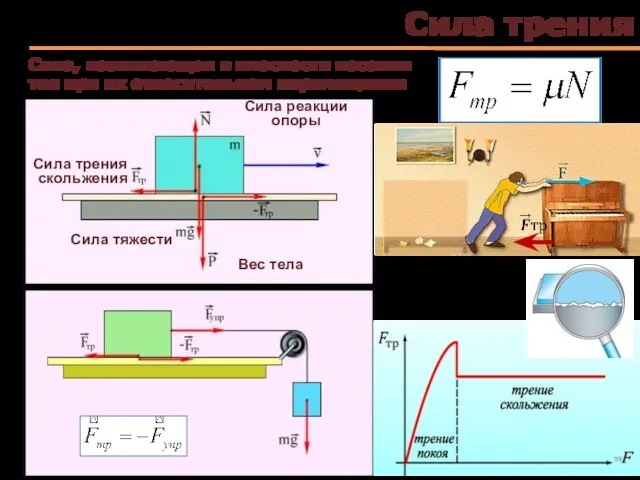
- 48. Силы трения появляются при перемещении соприкасающихся тел или их частей друг относительно друга Силы трения Внешнее
- 49. Сила трения Сила, возникающая в плоскости касания тел при их относительном перемещении Сила реакции опоры Сила
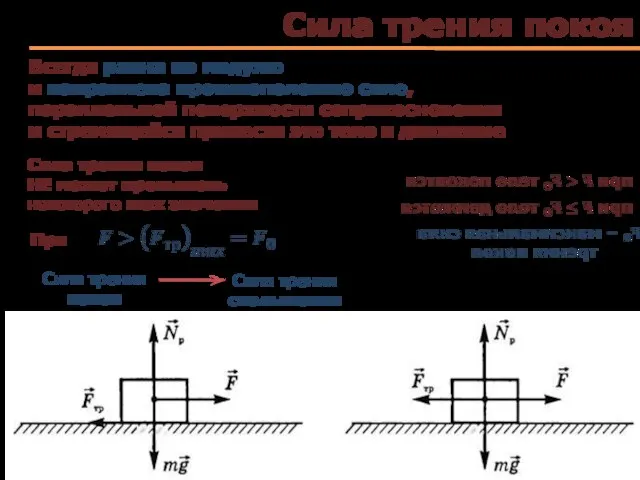
- 50. Сила трения покоя
- 51. Сила трения покоя Всегда равна по модулю и направлена противоположно силе, параллельной поверхности соприкосновения и стремящейся
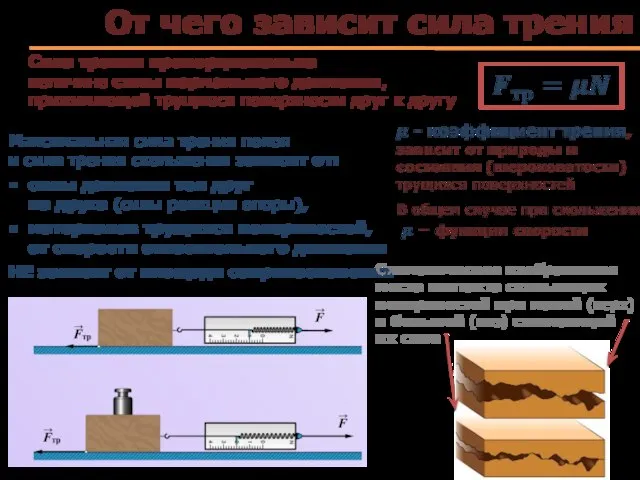
- 52. От чего зависит сила трения Сила трения пропорциональна величине силы нормального давления, прижимающей трущиеся поверхности друг
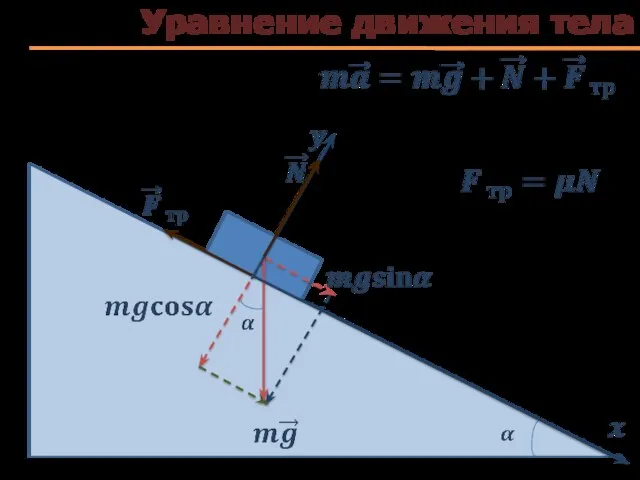
- 53. Уравнение движения тела
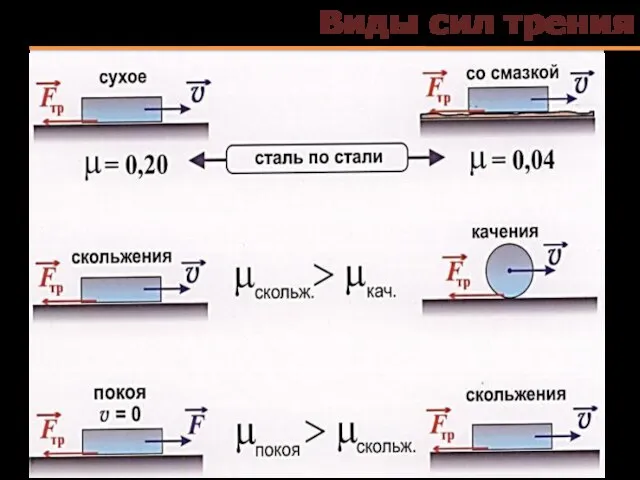
- 54. Виды сил трения
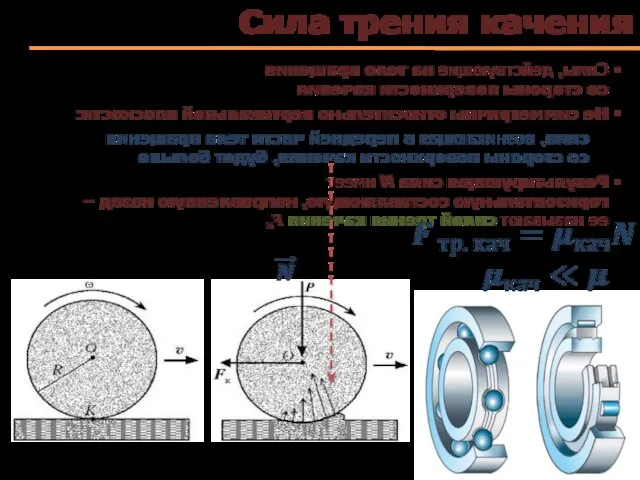
- 55. Сила трения качения
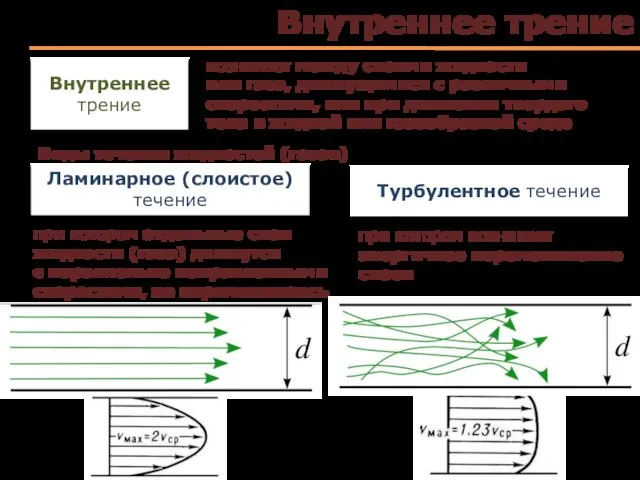
- 56. Внутреннее трение Виды течения жидкостей (газов) Внутреннее трение возникает между слоями жидкости или газа, движущимися с
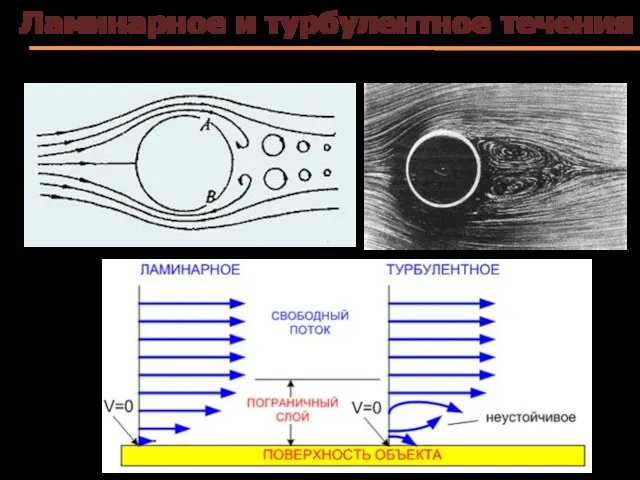
- 57. Ламинарное и турбулентное течения
- 58. Ламинарное и турбулентное течения
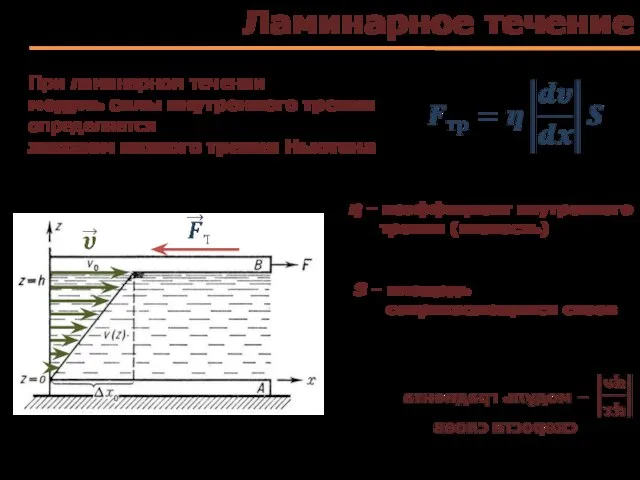
- 59. Ламинарное течение η – коэффициент внутреннего трения (вязкость) S – площадь соприкасающихся слоев При ламинарном течении
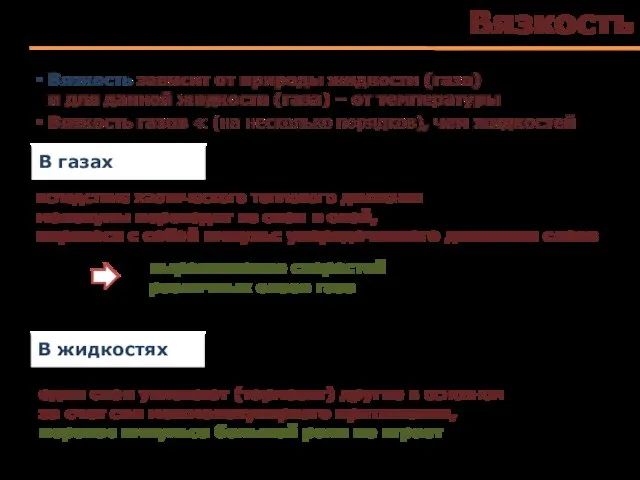
- 60. Вязкость одни слои увлекают (тормозят) другие в основном за счет сил межмолекулярного притяжения, перенос импульса большой
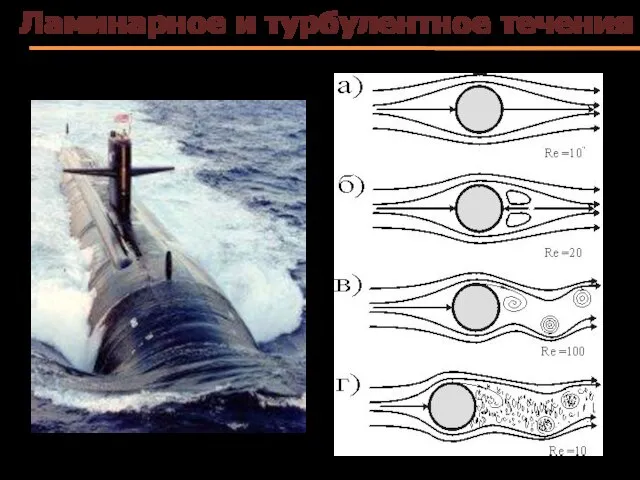
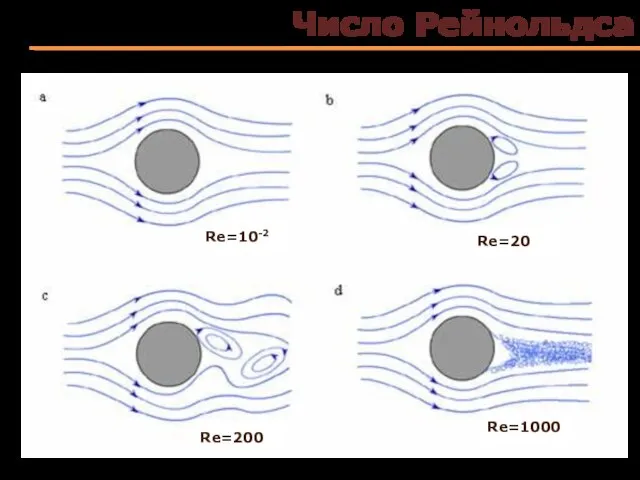
- 61. Число Рейнольдса Характер течения жидкостей (газов) или обтекания тел средой определяется безразмерным числом Рейнольдса Число Re
- 62. Число Рейнольдса Re=10-2 Re=20 Re=1000 Re=200
- 63. Закон Стокса Движение сферического тела в безграничной среде при малых значениях Re Движение сферического тела в
- 64. Контрольные вопросы Тело массой m подвешено на пружине жесткостью k в лифте, движущемся вверх А) с
- 65. Неинерциальные системы отсчета
- 66. Движение в неинерциальных СО Если система отсчета движется с ускорением, т.е. является неинерциальной, то законы Ньютона
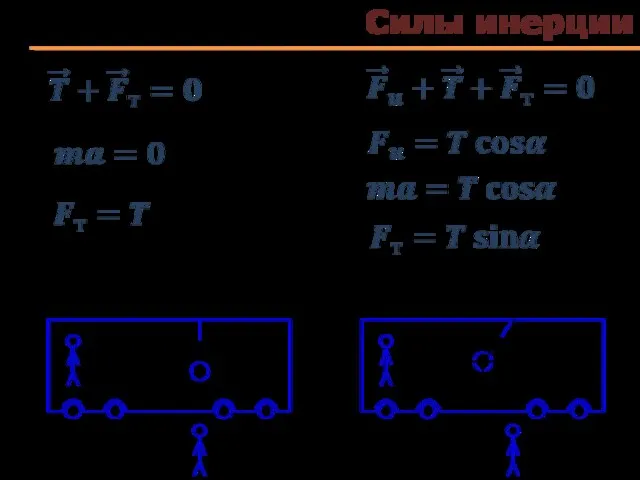
- 67. Силы инерции II з-н Н в неинерциальной СО: Воспользоваться законами Ньютона в неинерциальной СО можно, если
- 68. Силы инерции
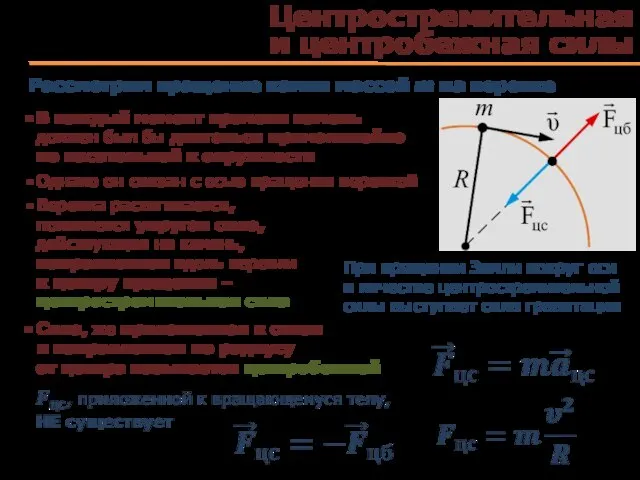
- 69. Центростремительная и центробежная силы Рассмотрим вращение камня массой m на веревке В каждый момент времени камень
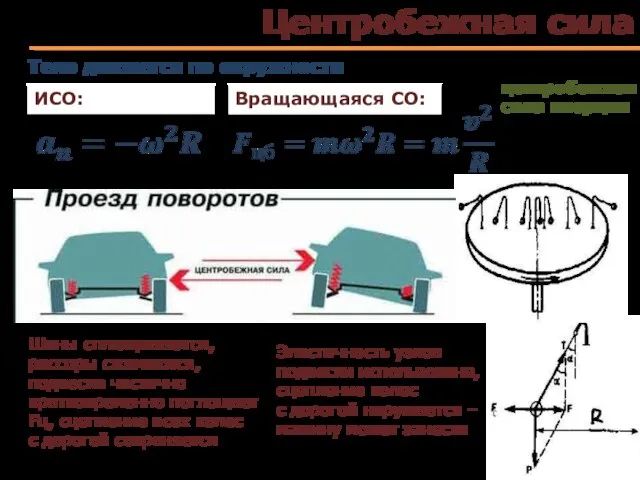
- 70. Центробежная сила ИСО: Вращающаяся СО: центробежная сила инерции Тело движется по окружности Шины сплющиваются, рессоры сжимаются,
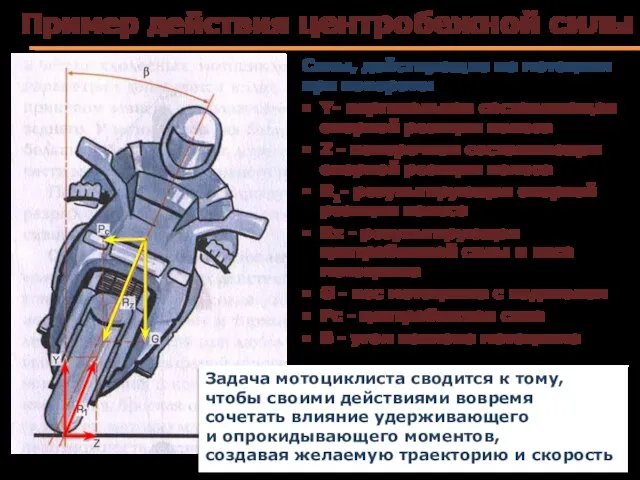
- 71. Пример действия центробежной силы Задача мотоциклиста сводится к тому, чтобы своими действиями вовремя сочетать влияние удерживающего
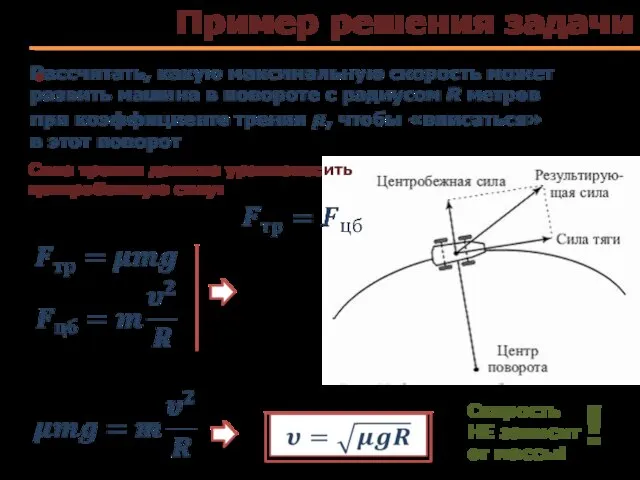
- 72. Пример решения задачи Скорость НЕ зависит от массы! Сила трения должна уравновесить центробежную силу: !
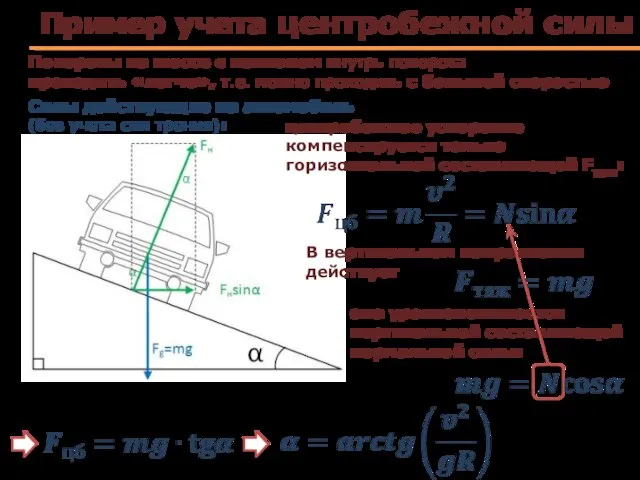
- 73. Пример учета центробежной силы Повороты на шоссе с наклоном внутрь поворота проходить «легче», т.е. можно проходить
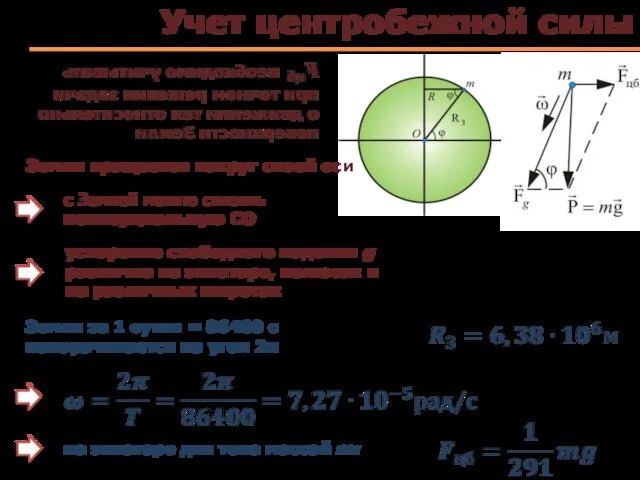
- 74. Учет центробежной силы Земля за 1 сутки = 86400 с поворачивается на угол 2π на экваторе
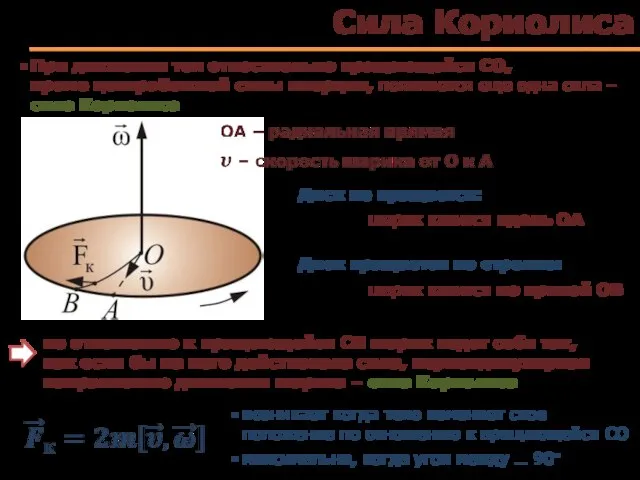
- 75. Сила Кориолиса При движении тел относительно вращающейся СО, кроме центробежной силы инерции, появляется еще одна сила
- 76. Гаспар-Гюстав Кориолис Французский математик, механик и инженер Также известен теоремой об ускорениях в абсолютном и относительном
- 77. Примеры проявления силы Кориолиса При свободном падении тел действие силы Кориолиса приводит к отклонению тел к
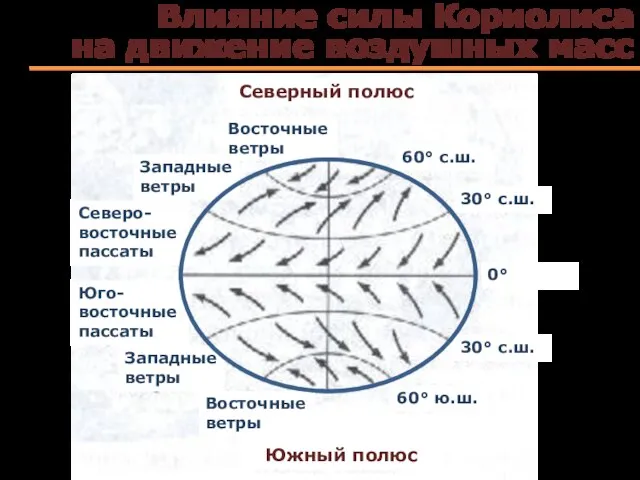
- 78. Влияние силы Кориолиса на движение воздушных масс Северный полюс Южный полюс Восточные ветры Западные ветры Северо-восточные
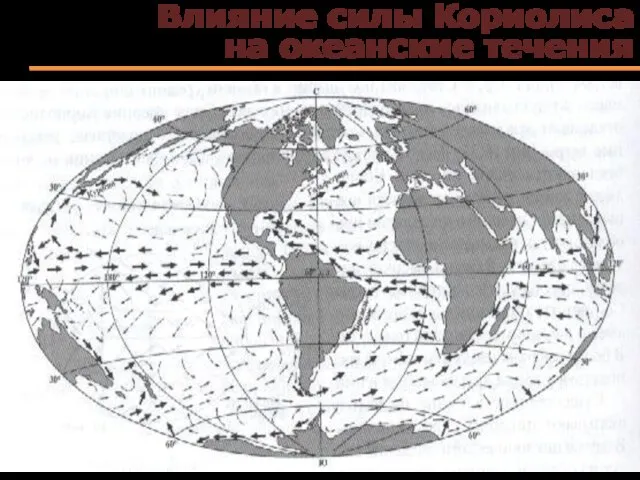
- 79. Влияние силы Кориолиса на океанские течения
- 80. Примеры проявления силы Кориолиса На северном полюсе сила Кориолиса все время направлена вправо по ходу маятника,
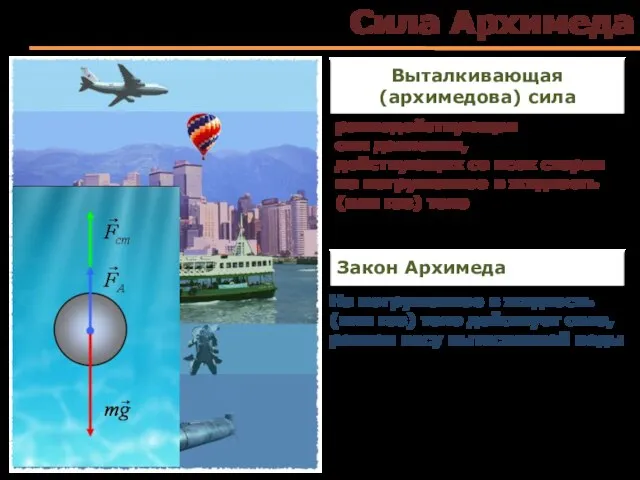
- 81. Сила Архимеда равнодействующая сил давления, действующих со всех сторон на погруженное в жидкость (или газ) тело
- 83. Скачать презентацию




























 Магнитные свойства материалов
Магнитные свойства материалов Консультация ГИА-9 по физике
Консультация ГИА-9 по физике Архитектурно-строительная акустика
Архитектурно-строительная акустика Презентация на тему Диффузия
Презентация на тему Диффузия  Дисперсия света
Дисперсия света Физика атомного ядра. Строение атомного ядра
Физика атомного ядра. Строение атомного ядра Естественная радиоактивность. Закон радиоактивного распада
Естественная радиоактивность. Закон радиоактивного распада Закон сохранения электрического заряда. Закон Кулона
Закон сохранения электрического заряда. Закон Кулона Строение атома. Состав атомных ядер. Изотопы. (8 класс)
Строение атома. Состав атомных ядер. Изотопы. (8 класс) Машина и механизм
Машина и механизм Презентация на тему Химические действия света (11 класс)
Презентация на тему Химические действия света (11 класс)  Значение режима смазывания для увеличения долговечности работы машин и механизмов
Значение режима смазывания для увеличения долговечности работы машин и механизмов Теплопередача через однослойную стенку
Теплопередача через однослойную стенку f3c279363c6051c6009ac4b1a3800ded
f3c279363c6051c6009ac4b1a3800ded Движение тела по окружности с постоянной по модулю скорости
Движение тела по окружности с постоянной по модулю скорости Классификация зубчатых передач
Классификация зубчатых передач Механическая работа и мощность
Механическая работа и мощность Электроэнергетические системы и сети. Определение параметров элементов электрической сети
Электроэнергетические системы и сети. Определение параметров элементов электрической сети Теория возмущений
Теория возмущений Понятие о цветовом пространстве на примере RGB. Цвет как вектор. Изменение яркости и насыщенности
Понятие о цветовом пространстве на примере RGB. Цвет как вектор. Изменение яркости и насыщенности ВПР. ВА и НКК. Лекция 3
ВПР. ВА и НКК. Лекция 3 Презентация_Sintecon_хроматография_краткая_обо_всем
Презентация_Sintecon_хроматография_краткая_обо_всем Курс физики. Введение
Курс физики. Введение Механические колебания
Механические колебания Механическая работа
Механическая работа Prezentatsia_8
Prezentatsia_8 Єдиний шлях, який веде до знань – це діяльність
Єдиний шлях, який веде до знань – це діяльність Тепловые двигатели. Виды двигателей
Тепловые двигатели. Виды двигателей