Физический маятник

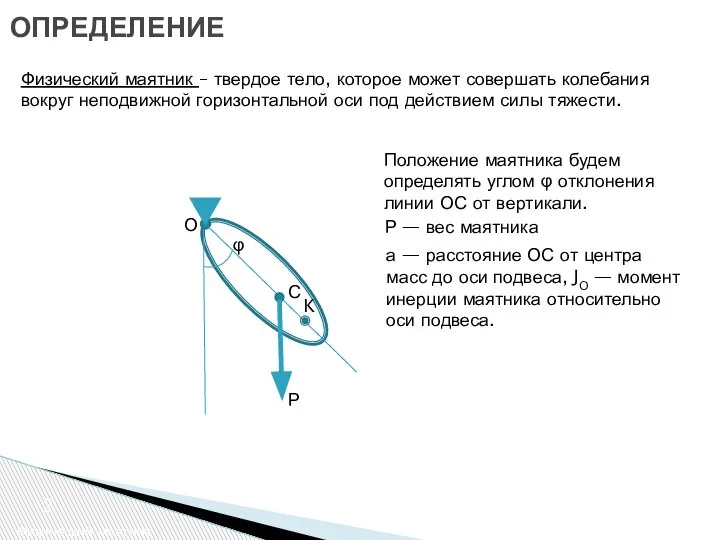
ОПРЕДЕЛЕНИЕ
Физический маятник
Физический маятник – твердое тело, которое может совершать колебания вокруг неподвижной горизонтальной оси под действием силы тяжести.
Положение маятника будем определять углом φ отклонения линии ОС от вертикали.
Р — вес маятника
а — расстояние ОС от центра масс до оси подвеса, JO — момент инерции маятника относительно оси подвеса.

ЗАКОН КОЛЕБАНИЙ МАЯТНИКА
Физический маятник
Для определения закона колебаний маятника воспользуемся дифференциальным уравнением вращательного движения.
В данном случае Mo= -P a sin φ, т.к. при φ <0 момент положителен, а при φ >0 момент отрицателен.
Ограничимся рассмотрением малых колебаний маятника, считая угол малым и приближенно , тогда уравнение примет вид:
Это уравнение совпадает по виду с дифф. Уравнением свободных прямолинейных колебаний, следовательно его общим решением будет:
Закон колебания при данных условиях:

СЛЕДСТВИЕ. ПРИВЕДЕННАЯ ДЛИНА
Физический маятник
Малые колебания физического маятника являются гармоническими, период колебаний маятника (при замене k) определяется формулой:
Т.е. при малых колебаниях период не зависит от начального угла.
При длине l1 период колебаний математического маятника совпадает с периодом колебаний соответствующего физического маятника.
Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

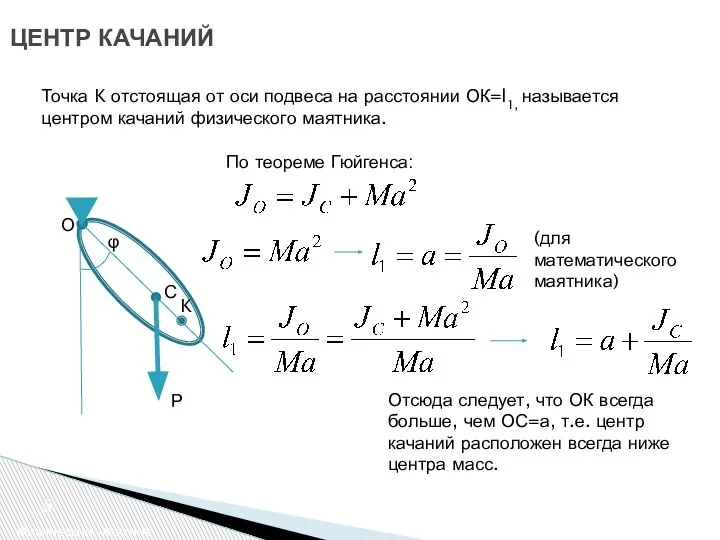
ЦЕНТР КАЧАНИЙ
Физический маятник
Точка K отстоящая от оси подвеса на расстоянии ОК=l1, называется центром качаний физического маятника.
По теореме Гюйгенса:
Отсюда следует, что ОК всегда больше, чем ОС=а, т.е. центр качаний расположен всегда ниже центра масс.
(для математического маятника)

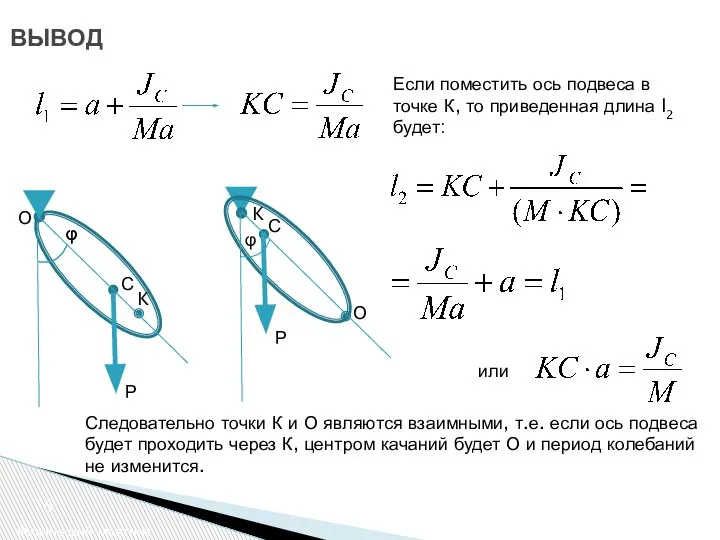
ВЫВОД
Физический маятник
Если поместить ось подвеса в точке К, то приведенная длина l2 будет:
Следовательно точки К и О являются взаимными, т.е. если ось подвеса будет проходить через К, центром качаний будет О и период колебаний не изменится.
или

Принцип Д’Аламбера
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА

Жан Леро́н Д’Аламбе́р
(16.11 1717 — 29.10 1783)
французский учёный-энциклопедист.
философ, математик и механик.
Член
Парижской академии наук(1740)
Французской академии наук(1754)
Петербургской академии(1764) и других академий наук.
Принцип Д’Аламбера
8

В каждый момент движения материальной точки активные силы, реакции связей и сила инерции образуют уравновешенную систему сил.
Принцип Даламбера для материальной точки:
9
Принцип Д’Аламбера
Введем вектор силы инерции точки и назовем введенный вектор Даламберовой или просто силой инерции. Эта сила - фиктивная.

10
Принцип Д’Аламбера
Запишем второй закон Ньютона:
Теперь если ввести, помимо всех внутренних и внешних сил фиктивную силу инерции, то ...
Сила инерции данной точки уравновешивает все приложенные к ней внутренние и внешние силы.
иначе:

Принцип Д’Аламбера
11
Пример:
Груз массой m опускается равноускоренно с помощью невесомого троса, перекинутого через блок, и за время t проходит расстояние L. Определить силу натяжения троса.

Принцип Даламбера для механической системы:
Принцип Д’Аламбера
12
Для движущейся механической системы в любой момент времени геометрическая сумма главных векторов внешних активных сил, сил реакций связей и сил инерции равна нолю; геометрическая сумма главных моментов внешних активных сил, реакций связей и сил инерции равна нулю.

Принцип Д’Аламбера
13
- главный вектор активных сил
- главный вектор реакций связей
- главный вектор сил инерции
главный момент активных сил
- главный момент реакций связей.
- главный момент сил инерции

Принцип Д’Аламбера
14
Сложим все уравнения полученной системы:
или

ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ
СИЛ ИНЕРЦИИ
Принцип Д’Аламбера
12
Как определить эти величины?
Теорема об изменении момента
импульса