Динамика и безопасность ядерных реакторов

Динамика и безопасность ЯР. Введение.
ВВЕДЕНИЕ
ОСНОВНАЯ ЗАДАЧА ФИЗИКИ ЯР – определение количества (потока) нейтронов в любой точке пространства активной зоны ЯР в любой момент времени. Так как мощность ЯР
P ~ Ф,
то, изменяя поток, мы управляем ЯР.
Как известно, в общем случае Ф = f (r, E, Ω, t).
Используя диффузионно-возрастное приближение, а также многогрупповой подход, для каждой энергетической группы нейтронов в АЗ
Ф = f (r, E, Ω, t) → Ф = f (r, t).

Динамика и безопасность ЯР. Введение.
Кроме того, ранее рассматривался ядерный реактор, который находится в критическом состоянии с неизменным во времени распределением потоков нейтронов. Следовательно, такой реактор имел и неизменную во времени мощность. Это означает
Ф = f (r,t) → Ф = f (r).
Это важная составляющая управления ЯР, т.к. большую часть времени работы реактор находится в критическом состоянии.
При этом нужно учитывать, что реактор имеет загрузку топлива, много большую, чем критическая. В противном случае реактор не обеспечивает необходимого времени работы.

Динамика и безопасность ЯР. Введение.
Такое положение приводит к необходимости влиять на поток нейтронов с помощью стержней управления. При этом происходит выгорание топлива и изменение температуры компонентов АЗ. Все это говорит о том, что в реальности ядерный реактор всегда находится в нестационарном состоянии.
Таким образом, мы имеем дело с динамикой ЯР – областью физики ЯР, основной задачей которого является описание поведения ЯР во времени при условии изменении внутреннего состояния реактора.
Динамика рассматривает нестационарные процессы, обусловленные как внешними воздействиями, так и изменением физических свойств активной зоны (внутренние воздействия), с учетом их взаимного и совокупного влияния на спектр и баланс нейтронов.

Динамика и безопасность ЯР. Введение.
К внешним воздействиям относится воздействия, вызванные применением стержней регулирования (пуск, остановка, маневрирование мощностью). Закономерности влияния таких воздействий изучаются в рамках кинетики ЯР – области физики ЯР, основной задачей которой является описание поведения реактора во времени при условии постоянства внутреннего состояния реактора.
Кинетика ЯР рассматривает изменение плотности потока нейтронов (мощности реактора) как реакцию на внешнее воздействие, приводящее к изменению баланса нейтронов в АЗ (например, перемещение регулирующих органов).

Динамика и безопасность ЯР. Введение.
Изменение физических свойств активной зоны (внутреннее воздействие) обусловлено:
Изменением температуры материалов активной зоны в процессе эксплуатации.
Выгоранием ядерного топлива, следствием которого являются:
накопление продуктов деления (отравление, шлакование ЯР);
образование трансурановых элементов.
Процессы выгорания топлива происходят сравнительно медленно в широком временном диапазоне: от часов (отравление) до сотен суток. Влияние внешних воздействий и изменение температуры осуществляются достаточно быстро (секунды, минуты).

Динамика и безопасность ЯР. Введение.
Все внешние и внутренние воздействия проявляются совместно и приводят к изменению мощности реактора во времени.
При всех изменениях в работе ЯР становится важной безопасность ядерного реактора.
Безопасность ядерного реактора – состояние ЯР, при котором действие внешних и внутренних факторов не приводит к ухудшению работы реактора или к невозможности его функционирования.

Разделы курса
1. Кинетика ядерного реактора.
2. Изменение нуклидного состава топлива в активной зоне ядерного реактора.
3. Температурные эффекты в ядерном реакторе.
4. Безопасность ядерного реактора.
Динамика и безопасность ЯР. Введение.

Основная литература
1. Копосов Е. Б. Кинетика ядерных реакторов: учебное пособие / Е. Б. Копосов. – М.: МГТУ им. Н.Э. Баумана, 2015.
2. Бартоломей Г.Г, Бать Г.А., Байбаков В.Д., Алтухов М.С. Основы теории и методы расчета ядерных энергетических реакторов. – М.: Энергоатомиздат, 1989.
3. Самойлов О.В., Усынин Г.Б., Бахметьев А.М. Безопасность ядерных энергетических установок. – М.: Энергоатомиздат, 1989.
4. Владимиров В.И. Практические задачи по эксплуатации ядерных реакторов. – М.: Изд-во «Либроком», 2009.
Динамика и безопасность ЯР. Введение.

Дополнительная литература
Глесстон С., Эдлунд М. Основы теории ядерных реакторов. – М.: Изд-во иностранной литературы, 1954.
Кесслер Г. Ядерная энергетика. – М.: Энергоатомиздат, 1968.
Камерон И. Ядерные реакторы. – М.: Энергоатомиздат, 1987.
Кузнецов В.А. Судовые ядерные энергетические установки. – Л.: Судостроение, 1989.
Динамика и безопасность ЯР. Введение.

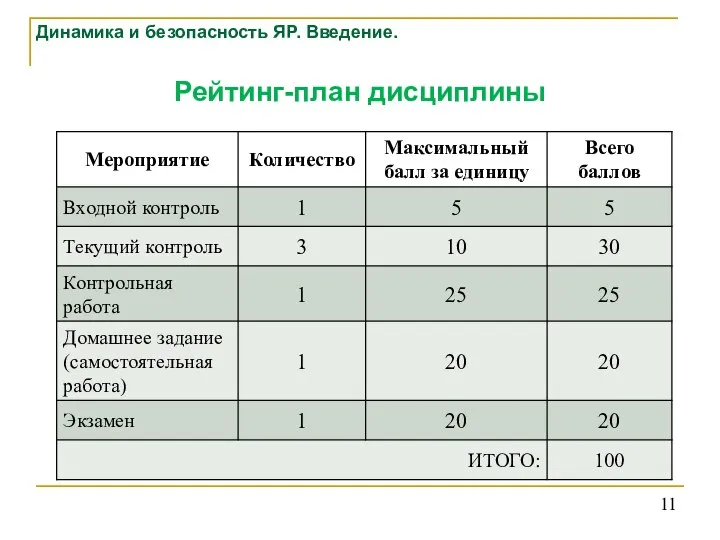
Рейтинг-план дисциплины
Динамика и безопасность ЯР. Введение.

1. Кинетика ядерного реактора
1.1. Основные понятия и приближения.
1.2. Элементарное уравнение кинетики.
1.3. Среднее время жизни нейтронного поколе-ния в реакторе.
1.4. Анализ кинетики реактора с учетом запаз-дывающих нейтронов.
1.5. Единицы измерения реактивности.
1.6 Основные положения кинетики подкритичес-кого реактора.*
* Вопрос рассмотреть самостоятельно.
Динамика и безопасность ЯР. Кинетика ядерного реактора.

1.1. Основные понятия и приближения
Развитие цепной реакции деления в АЗ ЯР характеризуется величиной kэф= k∞∙P, которая учитывает как размножающие свойства среды через k∞, так и геометрию среды через P.
Как отмечалось, реальный реактор всегда находится в нестационарном состоянии. Отсюда возникает необходимость измерять степень отклонения состояния реактора от критического. Для этого в общем случае используют ряд характеристик:
1. Избыточный коэффициент размножения (абсолютная реактивность, коэффициент избыточной мультипликации):
.
Динамика и безопасность ЯР. Кинетика ядерного реактора.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
По определению , где Nn+1 и Nn – число нейтро-нов следующего и данного поколения, соответственно. Тогда, учитывая, что Nn+1 = Nn ± ΔN, где ΔN – изменение числа нейтронов при переходе из поколения в поколение:
.
Избыточный коэффициент размножения показывает абсолютное отклонение kэф от единицы (критического состояния) и имеет физический смысл: относительное изменение количества нейтронов в следующем поколении к общему количеству нейтронов данного поколения. ∆kэф безразмерна, для анализа кинетики используется достаточно редко.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
2. Реактивность – ρ. По определению .
Переходя к числу нейтронов того или иного поколения получим:
.
В итоге реактивность показывает относительное отклонение kэф от единицы (критического состояния) и имеет физический смысл: относительное изменение количества нейтронов в следующем (новом) поколении.
Если в реакторе kэф → 1, то ρ ≈ ∆ kэф.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Для анализа нестационарных процессов в ЯР удобнее пользоваться именно понятием реактивности:
Во-первых, реактивность может легко и удобно являться мерой состояния реактора: подкритическому состоянию реактора соответствует kэф<1 и ρ < 0; в критическом реакторе kэф = 1 и ρ = 0 ; надкритическому состоянию реактора соответствует kэф>1 и ρ > 0.
Во-вторых, что самое важное даже при небольшом отклонении ρ от критического состояния изменения относительно критического значения (ноль) значительно больше, чем изменения kэф относительно того же критического значения (единица).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
3. Запас реактивности реактора (ЗР) – ρз (t)
Это величина положительной реактивности, которая создаётся за счёт загрузки в активную зону сверхкритического количества ядерного топлива и нейтрализуется введением в активную зону компенсирующих поглотителей и предназначается для обеспечения требуемой кампании реактора.
ЗР – это величина положительной реактивности, которая могла бы быть высвобождена сразу при мысленном (только мысленном!) удалении из активной зоны всех компенсирующих поглотителей.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
ЗР реактора нужен для поддержания реактора в критическом состоянии при работе его на постоянном уровне мощности в течение всей кампании и для компенсации потерь реактивности реактора в процессе его работы.
Однако некоторые процессы в реакторе протекают очень быстро и требуют столь же быстрых мер по компенсации возникающих изменений реактивности. Следовательно, в величине ЗР должна быть такая его часть, которая позволяла бы оператору (или системе автоматики) быстро реагировать на любые быстропротекающие изменения реактивности реактора и компенсировать их с целью поддержания критического режима работы реактора на заданном уровне мощности.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Часть запаса реактивности, компенсируемая одними подвижными поглотителями в реакторе, называется оперативным запасом реактивности (ОЗР)
Оперативной эта часть общего запаса реактивности названа,
во-первых, потому, что она находится в распоряжении оператора реакторной установки (перемещением стержней-поглотителей в активной зоне занимается оператор),
во-вторых, потому, что эти перемещения поглотителей могут производиться достаточно быстро (оперативно), что и обеспечивает быструю компенсацию изменений реактивности реактора в некоторых переходных процессах.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Величина запаса реактивности в продолжение всей кампании активной зоны реактора, уменьшается.
Но в любой момент кампании она складывается: из оперативного запаса реактивности, из запасов реактивности, компенсируемых неподвижными (выгорающими) поглотителями и жидким поглотителем (борной кислотой в воде, содержащейся в объёме активной зоны реактора):
ρз (t) = ρзоп(t) + ρзвп(t) + ρзж(t).

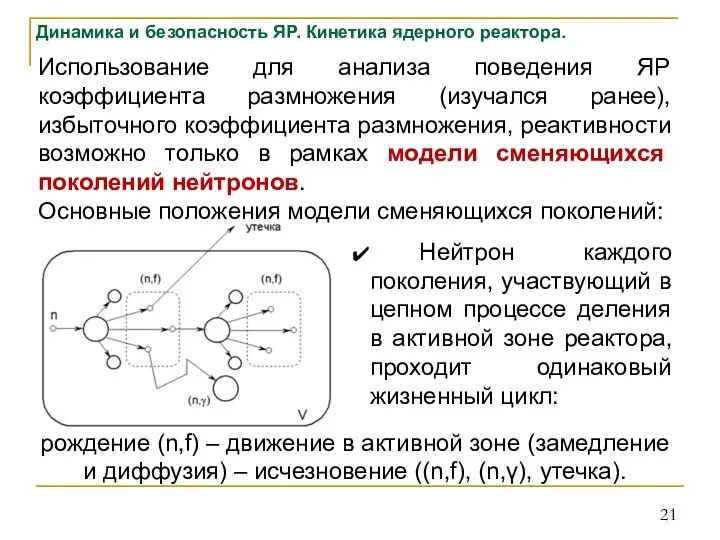
Использование для анализа поведения ЯР коэффициента размножения (изучался ранее), избыточного коэффициента размножения, реактивности возможно только в рамках модели сменяющихся поколений нейтронов.
Основные положения модели сменяющихся поколений:
Нейтрон каждого поколения, участвующий в цепном процессе деления в активной зоне реактора, проходит одинаковый жизненный цикл:
рождение (n,f) – движение в активной зоне (замедление и диффузия) – исчезновение ((n,f), (n,γ), утечка).
Динамика и безопасность ЯР. Кинетика ядерного реактора.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Нейтроны каждого поколения рождаются одновременно.
Нейтроны каждого поколения живут определенное одинаковое время l (время жизни нейтронного поколения).
Нейтроны каждого поколения одновременно заканчивают свой жизненный цикл, участвуя в реакции деления и, тем самым, порождая нейтроны следующего поколения.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
В кинетики реакторов используют следующие приближения.
1. Рассматривается модель “точечного реактора”.
Это означает, что нас интересует поведение реактора во времени как устройства в целом, а не пространственное изменение потоков. Формально это сводится к тому, что в любой момент времени форма пространственного распределения нейтронного потока остается постоянной и близко к критическому состоянию реактора.
2. Рассматривается лишь скачкообразное изменение реактивности. После скачка значение реактивности остается постоянным во времени:
ρ (t) = cons`t ≠ 0.

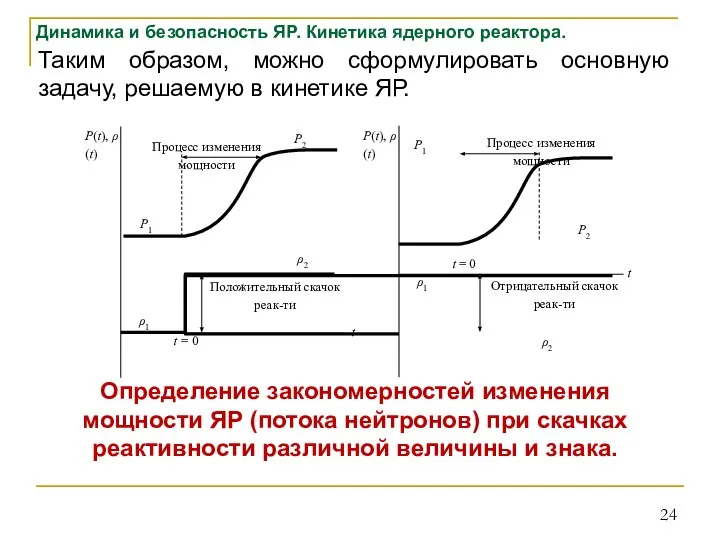
Динамика и безопасность ЯР. Кинетика ядерного реактора.
Таким образом, можно сформулировать основную задачу, решаемую в кинетике ЯР.
Определение закономерностей изменения мощности ЯР (потока нейтронов) при скачках реактивности различной величины и знака.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
1.2. Элементарное уравнение кинетики
Пусть реактор в начальный момент времени (t0 = 0) был критичен (то есть эффективный коэффициент размножения в нём был равен единице, а реактивность – нулю). При этом средний поток тепловых нейтронов в ЯР составлял Ф(t).
Пусть ЯР была сообщена скачком некоторая величина реактивности (для определённости - реактивности положительного знака), вследствие чего эффективный коэффициент размножения kэф поднимется над единицей на некоторую величину Δkэф – избыточный коэффициент размножения.
Тогда величина потока в ЯР станет kэф ·Ф(t).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
kэфФ(t) - Ф(t) = Ф(t) (kэф - 1) = Ф(t) Δkэф.
Введем в рассмотрение (пока формально) величину l – время жизни нейтронного поколения.
Тогда скорость изменения потока нейтронов за время l будет равно:
. (1)
Дифференциальное уравнение (1) называется элементарное уравнение кинетики реактора (ЭУКР).
ЭУКР - дифференциальное уравнение с разделяющимися переменными:
. (2)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Проведя прямое интегрирование (2) при начальных условиях t = 0 Ф(0) = Ф0, получим решение ЭУКР:
. (3)
Выражение (3) определяет закон изменения потока нейтронов (мощности ЯР) во времени после скачкообразного изменения эффективного коэффициента размножения (введения реактивности).
При малых отклонениях состояния ЯР от критического kэф → 1, то ρ ≈ Δ kэф получаем:
.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Выражение (3) можно представить в следующем виде:
, (4)
где T = l∕∆kэф – период реактора. Из (4) можно определить физический смысл периода реактора: это время, в течение которого поток нейтронов (а значит и мощность) изменяются в е = 2,72 раза.
При введении положительной реактивности Т > 0. Если введена отрицательная реактивность, то Т < 0.
Чем выше величина периода Т, тем менее круто (более плавно) происходит изменение мощности при сообщении критическому реактору реактивности того или иного знака (и наоборот).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
В практике эксплуатации реакторов часто пользуются не периодом реактора, а периодом удвоения мощности Т2, под которым понимают время, в течение которого поток нейтронов (а значит и мощность) изменяется в 2 раза. Используя (4) можно найти связь периода удвоения и периода реактора:
.

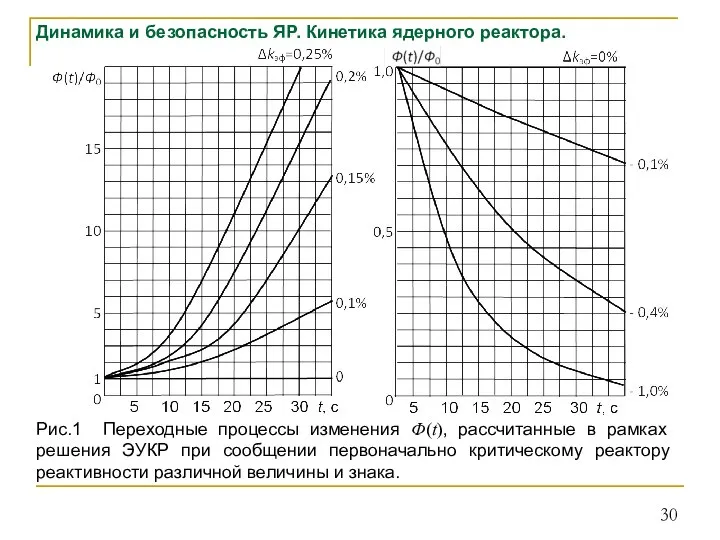
Динамика и безопасность ЯР. Кинетика ядерного реактора.
Рис.1 Переходные процессы изменения Ф(t), рассчитанные в рамках решения ЭУКР при сообщении первоначально критическому реактору реактивности различной величины и знака.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Выводы:
Переходный процесс изменения во времени среднего потока тепловых нейтронов в реакторе после сообщения первоначально критическому реактору реактивности любой величины и знака имеет экспоненциальный характер.
Чем больше абсолютная величина сообщаемой первоначально критичному реактору реактивности, тем круче, интенсивнее, протекают в реакторе переходные процессы изменения плотности нейтронов.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
1.3. Среднее время жизни нейтронного поколения в реакторе.
Сравнение результатов, полученных при решении ЭУКР, с переходными процессами в реальных реакторах показывает ряд существенных отличий. Например, решение ЭУКР не описывает наличие скачков мощности реактора в начальные моменты реальных переходных процессов.
Эти несоответствия подталкивают к мысли о том, что в ЭУКР что-то не учтено. И это что-то должно быть связано с величиной среднего времени жизни поколения нейтронов в реакторе l: иных характеристик самого реактора в ЭУКР нет.

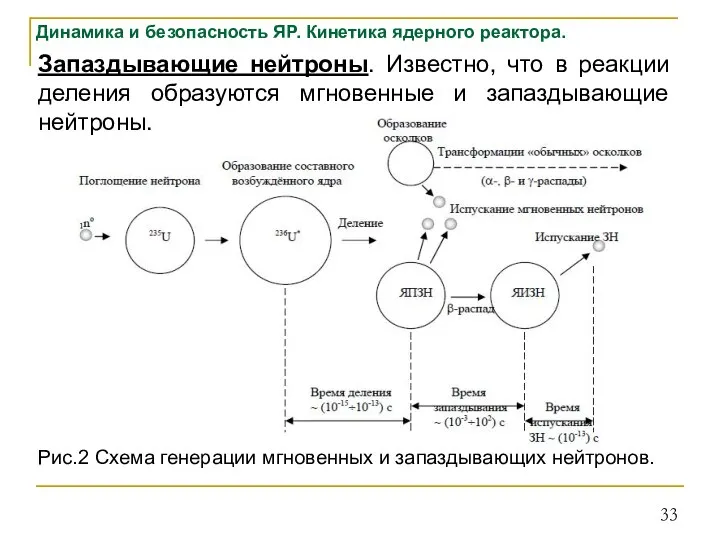
Динамика и безопасность ЯР. Кинетика ядерного реактора.
Запаздывающие нейтроны. Известно, что в реакции деления образуются мгновенные и запаздывающие нейтроны.
Рис.2 Схема генерации мгновенных и запаздывающих нейтронов.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Мгновенные нейтроны образуются непосредственно в реакции деления. Запаздывающие нейтроны возникают внутри бета-радиоактивных цепочек распада продуктов деления.
Ядра, являющиеся родоначальниками радиоактивных цепочек, в которых образуются запаздывающие нейтроны, называются ядрами-предшественниками запаздывающих нейтронов (ЯПЗН), а ядра, непосредственно испускающие запаздывающие нейтроны – ярами-излучателями запаздывающих нейтронов (ЯИЗН).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Ядро-излучатель испускает запаздывающий нейтрон практически мгновенно (время жизни ядра порядка 10-14 с), но со значительным опозданием по отношению к моменту деления, поэтому время запаздывания практически полностью совпадает со временем жизни ядра-предшественника.
Встречаются более 60 типов осколков деления, которые, способны испускать запаздывающие нейтроны. Не все ЯПЗН играют существенную роль в процессе размножения нейтронов в реакторе:
некоторые имеют малый выход в реакции деления;
некоторые имеют очень малый период полураспада (ЗН не отличаются от мгновенных);
некоторые имеют очень большой периодом полураспада (ЗН образуются за пределами переходных процессов).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Таким образом, остается не более пятнадцати ЯПЗН, которые дают более 98% всех генерируемых запаздывающих нейтронов.
Количество запаздывающих нейтронов определяется долей запаздывающих нейтронов β – это среднее число запаздывающих нейтронов, приходящееся на один получаемый нейтрон деления в критическом реакторе бесконечных размеров (β всегда много меньше 1).
Например, в делениях ядер 235U из каждых 10000 нейтронов деления лишь 64 нейтрона будут запаздывающими, а остальные 9936 нейтронов - мгновенными (или 0.64% всех нейтронов - запаздывающие, а остальные 99.36% нейтронов - мгновенные).

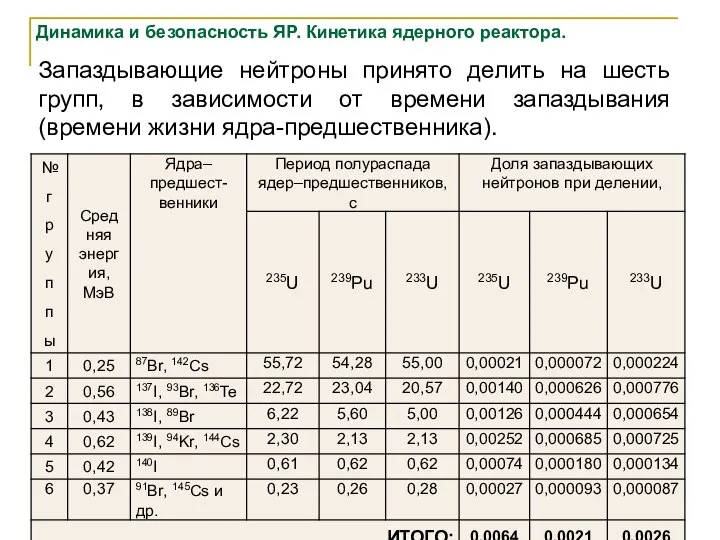
Динамика и безопасность ЯР. Кинетика ядерного реактора.
Запаздывающие нейтроны принято делить на шесть групп, в зависимости от времени запаздывания (времени жизни ядра-предшественника).

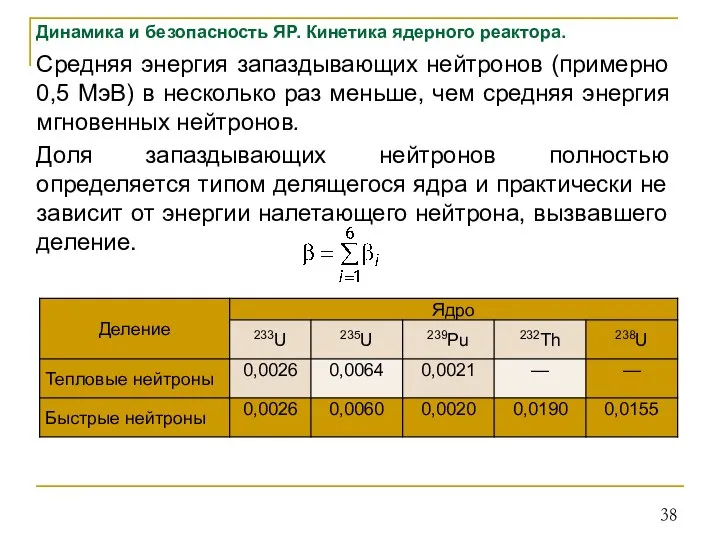
Динамика и безопасность ЯР. Кинетика ядерного реактора.
Средняя энергия запаздывающих нейтронов (примерно 0,5 МэВ) в несколько раз меньше, чем средняя энергия мгновенных нейтронов.
Доля запаздывающих нейтронов полностью определяется типом делящегося ядра и практически не зависит от энергии налетающего нейтрона, вызвавшего деление.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Средним временем жизни нейтронного поколения l в ЯР будем называть промежуток времени от момента поглощения в топливе делящего нейтрона n-го поколения до момента поглощения нейтрона следующего n+1 поколения.
Время запаздывания lзап практически полностью определяется временем жизни ядер-предшественников*.
* Выражения и оценки для среднего времени жизни получить самостоятельно

Динамика и безопасность ЯР. Кинетика ядерного реактора.
1.4. Анализ кинетики реактора с учетом запаздывающих нейтронов
Ранее мы анализировали кинетику ЯР на основании элементарного уравнения кинетики. Однако в действительности временная зависимость потока нейтронов гораздо сложнее, т.к. необходим корректный учет запаздывающих нейтронов.
Уравнение обратных часов (УОЧ). Для получения УОЧ запишем нестационарное уравнение диффузии:
где Q(r,t) – функция источника нейтронов; V – скорость нейтронов. Разделим переменные Ф(r,t)= Ф(r)·Ф(t), Q(r,t)= Q(r)·Q(t) и подставим это в записанное уравнение диффузии:

Динамика и безопасность ЯР. Кинетика ядерного реактора.
(1)
Пусть состояние ЯР близко к критическому. В этом случае для пространственного распределения потока нейтронов будет справедливо уравнение реактора:
отсюда
Полученное подставим в (1), разделив обе его части на Ф(r):
(1*)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
В выражении (1*) проделаем следующие действия:
Т.к. Q(r) прямо пропорциональна Ф(r), то Q(r)∕Ф(r)=К (константа). Обозначим К·Q(t) = S (t).
Разделим обе части уравнения на Σa.
Вспомним, что D ∕ Σa =L2 (квадрат длины диффузии).
Установим, что 1 ∕ (VΣa)=l0 – время жизни нейтрона (нейтронного поколения) в бесконечной среде (Почему?).
В итоге получим уравнение вида:
(2)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Рассмотрим функцию источника S(t)*. При наличии запаздывающих нейтронов, доля которых равна β, функция источника может быть представлена как суперпозиция источника тепловых нейтронов, возникающих при замедлении мгновенных и запаздывающих нейтронов:
S(t)= Sмг(t)+Sзап(t).
Подставим записанные функции источников нейтронов в выражение (2) и приведем подобные:
. (3)
Для окончательной постановки задачи необходимо уравнение (3) дополнить m уравнениями баланса изменения количества ЯПЗН каждой группы запаздывающих нейтронов.
* Функцию источника и баланс ЯПЗН рассмотреть самостоятельно

Динамика и безопасность ЯР. Кинетика ядерного реактора.
В математической записи уравнение баланса ЯПЗН имеет вид: . (4)
Таким образом, для решения поставленной задачи необходимо совместно рассмотреть уравнение (3) и m уравнений типа (4):
; (3)
. (4)
Частные решения системы уравнений (3)-(4) будем искать в виде:
Ф(t) = Ф0 exp (ωt); (5)
Ci(t) = Ci0 exp (ωt), (6)
где Ф0 и Ci0 – поток нейтронов и концентрация ядер-предшественников в момент времени t = 0.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Подставим (5)–(6) в (4) и определим константу Ci0 :
. (7)
Подставим выражения (5) – (7) в уравнение (3):
. (8)
В выражении (8) осуществим следующие операции:
разделим обе части на (L2B2+1);
вспомним, что ;
определим, что – время жизни нейтронов в
конечной среде (Почему?);
учтем, что , kэф – 1= ∆kэф и .

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Решая полученное уравнение относительно ρ (реактивность) получим уравнение вида:
. (9)
Уравнение (9) является характеристическим уравнением относительно ω. Решение этого уравнения дает те значения ω, при которых существуют решения нестационарного уравнения диффузии с учетом запаздывающих нейтронов (3), имеющие вид (5):
Ф(t) = Ф0 exp (ωt).
Графически представим решение полученного уравнения (9).

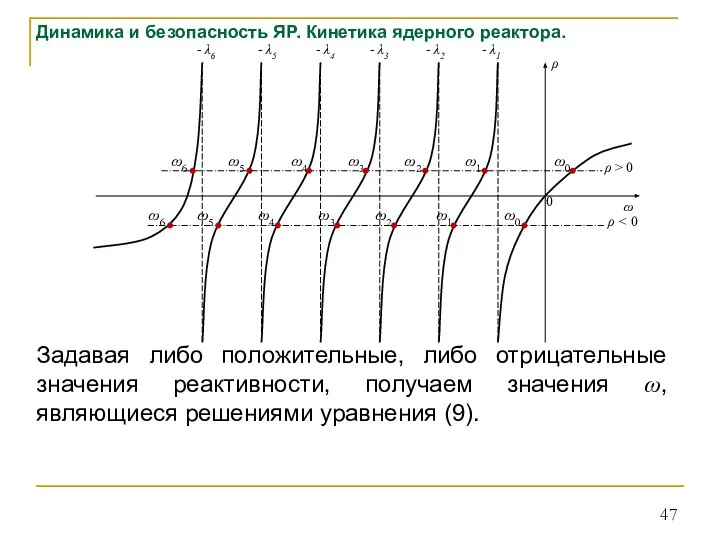
Динамика и безопасность ЯР. Кинетика ядерного реактора.
Задавая либо положительные, либо отрицательные значения реактивности, получаем значения ω, являющиеся решениями уравнения (9).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Проведем анализ представленного решения уравнения (9):
функция ρ (ω) имеет m+1 разрывов при ω → – λi ;
при любом положительном значении ρ существует m+1 (в нашем случае 7) корней уравнения (9), из которых m корней – отрицательны, один – положительный (ω0);
при любом отрицательном значении ρ все m+1 (в нашем случае 7) корней уравнения (9) отрицательны.
Таким образом, можно утверждать, что поток нейтронов во времени изменяется по закону:
. (10)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Пусть ρ >0. Тогда из решения уравнения (9) следует, что во всех слагаемых суммы (10), кроме первого, содержатся экспоненты с отрицательными показателями, т.е. с увеличением t эти слагаемые будут уменьшаться. Вклад каждого из них в сумму (10) существенен в течение промежутка времени, равного примерно соответствующему времени жизни ЯПЗН. Показатель экспоненты первого слагаемого суммы (10) всегда положителен ω0t >0. Это значит, что по прошествии времени после скачка реактивности, равного примерно времени жизни наиболее долгоживущих ЯПЗН, величина потока будет определяться практически лишь этим слагаемым:
. (11)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Используя данные таблицы о запаздывающих нейтронах, можно сказать, что время установления распределения (11) составляет десятки секунд.
В кинетике ЯР процесс изменения мощности ядерного реактора, который носит экспоненциальный характер (описывается выражением (11)), называется установившийся режим изменения мощности ЯР.
Процесс изменения мощности ядерного реактора, подчиняющийся распределению (10) называется переходный режим изменения мощности.
Сравнивая выражение (11) и решение ЭУКР видно, что период реактора равен . Таким образом, период реактора можно трактовать как период реактора в установившемся режиме изменения мощности ЯР.

Соответственно, Т носит название установившегося периода реактора (далее для более корректного рассмотрения установившийся период будем обозначать как Т0). По аналогии величины Ti =1 ∕ ωi
носят название переходных периодов ЯР.
В уравнении (9) перейдем от переменной ω к переменной Т (период):
(12)
Полученное уравнение (12) носит название уравнения обратных часов (УОЧ). Оно связывает период реактора и величину и знак введенной реактивности. При этом . (13)
Динамика и безопасность ЯР. Кинетика ядерного реактора.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Таким образом, для определения закономерностей изменения мощности ЯР (потока нейтронов) при введении той или иной реактивности необходимо рассчитать поток нейтронов по (13) с учетом УОЧ (12). Такие решения осуществляются численными методами и конечно же не дают качественного понимания всей картины кинетики ЯР. Для качественного анализа используют более упрощенные методы, одним из которых является приближение с одной группой запаздывающих нейтронов.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Итак, пусть имеется только одна группа запаздывающих нейтронов. Тогда, полагая, что реактор до возмущения находится в состоянии, близком к критическому, известное характеристическое уравнение (9) примет вид:
. (14)
Видно, что уравнение (14) представляет собой квадратное уравнение относительно параметра ω:
.
Решения этого квадратного уравнения достаточно несложно записать:
. (15)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Таким образом, уравнение (14) имеет два решения ω0 и ω1. Это означает, что поток нейтронов изменяется во времени по закону:
, (16)
аналогично, концентрация ядер-предшественников запаздывающих нейтронов будет изменяться во времени следующим образом:
, (17)
где А0, А1, В0, В1 – константы, определяемые из начальных условий: Ф(t = 0) = Ф0, С(t = 0) = С0.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Анализ кинетики ЯР при введении положительной реактивности малой величины.
Будем считать (пока формально!!!), что малыми положительными реактивностями являются реактивности, для которых 0 < ρ << β.
В этом случае величина , в квадратном корне решения (15) является малой величиной. Это позволяет квадратный корень в решении (15) разложить в ряд Маклорена. Тогда, ограничиваясь первым членом указанного разложения, решениями уравнения (15) являются:
; (18)
. (19)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Для однозначного определения потока нейтронов согласно выражению (16) необходимо определить коэффициенты А0 и А1. Это осуществляется путем совместного рассмотрения выражений (16)÷(19) с учетом начальных условий Ф(t = 0) = Ф0, С(t = 0) = С0. Без рассмотрения достаточно громоздких математических преобразований определим, что
;
.
Таким образом, закон изменения нейтронного потока во времени примет вид:
. (20)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Из (20) видно, что установившийся период реактора равен:
. (21)
Выражение (21) получено с учетом малости величины реактивности ρ << β. Проверку корректности можно провести в рамках рассмотрения 6 групп запаздывающих нейтронов. Для возьмем уравнение обратных часов (12) и запишем его для установившегося режима:
(22)
Если 0 < ρ << β, то T0 велик и T0 >>li=1/λi, отсюда T0 λi >>1.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Используя полученное условие для (22), выразим T0 в явном виде. Учтем, что время жизни мгновенных нейтронов много меньше времени запаздывания . Тогда выражение (22) примет вид:
, (23)
т.к. lρ – малая величина. Сравнивая (21) и (23) видно, что с точностью до одной группы запаздывающих нейтронов оба выражения идентичны.
Вернемся к анализу кинетики. Мы получили, что
в установившемся режиме изменения мощности ЯР
; (21)
в переходном режиме изменения мощности ЯР
. (24)
(см. выражение (20) с учетом исходного условия ρ << β)

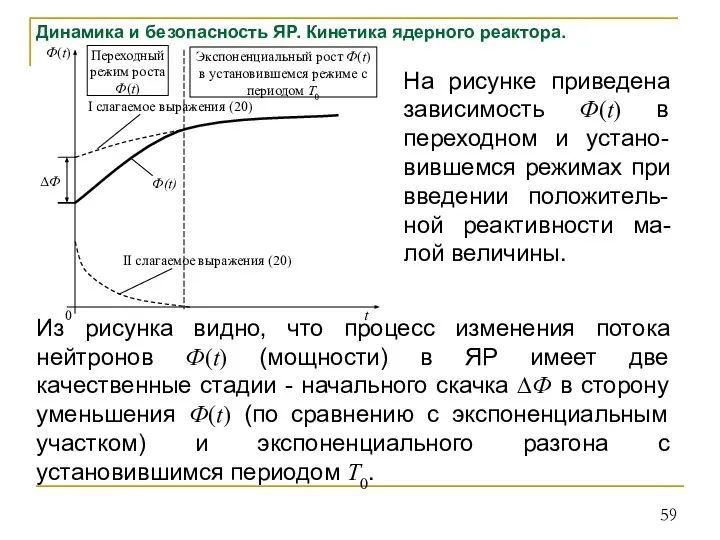
Динамика и безопасность ЯР. Кинетика ядерного реактора.
На рисунке приведена зависимость Ф(t) в переходном и устано-вившемся режимах при введении положитель-ной реактивности ма-лой величины.
Из рисунка видно, что процесс изменения потока нейтронов Ф(t) (мощности) в ЯР имеет две качественные стадии - начального скачка ∆Ф в сторону уменьшения Ф(t) (по сравнению с экспоненциальным участком) и экспоненциального разгона с установившимся периодом Т0.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
В первый момент времени (порядка десятых долей секунды) после введения малой положительной ρ изменение потока нейтронов почти полностью определяется вторым слагаемым выражения (20) (переходный режим). Это изменение происходит с периодом – выражение (24). Это означает, что при малых значениях положительной ρ запаздывающие нейтроны практически не участвуют в изменении потока нейтронов в начальный момент времени после скачка реактивности.
По истечении времени (порядка единиц секунды) второе слагаемое (переходной режим) в выражении (20) затухает, и поток нейтронов изменяется по закону:
.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Это соответствует установившемуся режиму разгона реактора при малых положительных значениях ρ с установившимся периодом – выражение (21).
Поведение реактора в этом случае определяется поведением запаздывающих нейтронов.
Таким образом, необходимо отметить одну важную особенность – резкий рост (практически скачком) потока нейтронов в переходном режиме разгона реактора и относительно слабый – в установившемся.
Дадим физическую интерпретацию полученных результатов.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Если реактор находился в критическом состоянии достаточно долго, то в нем доля запаздывающих нейтронов остается неизменной.
При введении малой положительной реактивности скорость реакции деления увеличивается, что приводит к увеличению количества ЯПЗН и количества мгновенных нейтронов. Вследствие того, что ЯПЗН испускают запаздывающие нейтроны с некоторым опозданием, то в первые моменты времени количество запаздывающих нейтронов остается практически таким же, каким было до введения реактивности. При этом растет число мгновенных нейтронов. Таким образом, доля запаздывающих нейтронов в общем количестве нейтронов уменьшается.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Следовательно, мгновенные нейтроны играют основную роль, наблюдается резкое увеличение потока нейтронов (это демонстрировалось при изучении ЭУКР).
В дальнейшем из-за малости введенной реактивности скорость образования мгновенных нейтронов увеличивается слабо, в то время скорость образования запаздывающих нейтронов начинает «догонять» скорость образования мгновенных нейтронов, т.к. в процессы распада все сильнее с течением времени включаются все более долгоживущие ЯПЗН. Таким образом, по прошествии некоторого промежутка времени доля запаздывающих нейтронов в общем количестве нейтронов начинает возрастать. Тем самым, как нам известно, скорость увеличения потока начинает падать, что дает возможность управлять этим процессом.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Анализ кинетики ЯР при введении положительной реактивности большой величины.
Будем считать (пока также формально!!!), что большими положительными реактивностями являются реактивности, для которых ρ >> β.
Тогда в рамках приближения одной группы запаздывающих нейтронов выражение для параметра ω, имеющего вид (15)
,
будет выглядеть следующим образом (с учетом малости произведения lλ):
.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Раскладывая квадратный корень в ряд Маклорена и ограничиваясь первым значащим слагаемым, полученное примет вид:
. (25)
Таким образом, в случае больших значений реактивности можно получить следующие значения параметра ω:
; (26)
. (27)
Сравнивая (26) и (27), видно, что ω0>>|ω1|.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Следовательно, для проведения качественного анализа кинетики ЯР, нет необходимости определять константы в законе изменения потока нейтронов во времени, т.к. в любой сколь угодно малый момент времени поток нейтронов практически полностью определяется первым слагаемым, описывающим установившийся режим (см. выражение (16)):
.
Это означает, что в случае введения больших положительных реактивностей переходный режим разгона практически отсутствует.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Для окончательного анализа необходимо определить Т0. Это можно сделать, рассматривая УОЧ, записанное для установившегося периода (выражение (22)):
Для больших ρ >> β установившийся период T0 мал и
T0 << li=1/λi, отсюда T0 λi << 1. В этом случае выражение (22) примет вид:
,
где . Выражая отсюда Т0, получим:
. (28)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Это означает, что запаздывающие нейтроны практи-чески не принимают участия в изменении потока нейтронов. На рисунке приведено изменение плотности
потока нейтронов во времени при различных значениях положительной реактивности. Видно, что при малых ρ изменение потока нейтронов во времени имеет «изломы», соответствующие наличию
переходных режимов, при больших ρ изменение потока происходит почти по прямой, что говорит о незначи-тельных переходных режимах разгона. То есть ЯР наращивает свою мощность теоретически с бесконеч-ной скоростью.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Дадим физическую интерпретацию полученного. При больших введенных положительных реактивностях скорость образования мгновенных нейтронов больше скорости образования запаздывающих нейтронов практически в любой момент времени после скачка реактивности. Следовательно, доля мгновенных нейтронов в общем количестве нейтронов все время растет, а доля запаздывающих нейтронов все время падает (говорят, что реактор «опережает» запаздывающие нейтроны). В этом случае наблюдается резкое почти по прямой увеличение потока, определяемое в основном мгновенными нейтронами. Нам известно, что такая ситуация не позволяет эффективно управлять реактором.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Мгновенная критичность реактора. Рассматривая кинетику ЯР с введенной положительной реактивностью мы заметили, что поведение реактора в случае малых ρ отличается от поведения ЯР при больших ρ. При этом мы сравнивали величину ρ в долей запаздывающих нейтронов β. Можно предположить, что β является некой мерой возможности управления реактором. Для доказательства этого введем понятие мгновенно критического реактора. Мгновенная критичность – это состояние реактора, при котором он становится критическим на одних мгновенных нейтронах. Определим условие, при котором наступает мгновенная критичность ЯР. Для этого воспользуемся известным уравнением диффузии с учетом запаздывающих нейтронов:

Динамика и безопасность ЯР. Кинетика ядерного реактора.
.
Т.к. в реакторе только мгновенные нейтроны, то третье слагаемое, описывающее источник запаздывающих нейтронов, можно исключить. При этом реактор находится в критическом состоянии, т.е. поток не должен изменяться во времени. Значит правая часть уравнения равна нулю. Следовательно, записанное уравнение диффузии примет вид (раскрывая все скобки):
. (29)
В выражении (29):
приведем подобные;
разделим обе части на Ф(t)·(1+L2B2);
вспомним, что .

Динамика и безопасность ЯР. Кинетика ядерного реактора.
В итоге получим
. (30)
Из определения реактивности
следует, что .
Подставим полученное в (30) и получим условие
ρ = β. (31)
Анализируя (31), видно, что ЯР становится мгновенно критичным тогда, когда ему сообщается положительная реактивность, большая или равная величине доли запаздывающих нейтронов:
ρ ≥ β. (32)
Условие (32) – условие мгновенной критичности ЯР (при котором возможет неуправляемый разгон ЯР).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Соответственно, при 0 < ρ < β реактор будет критичен или надкритичен на мгновенных и запаздывающих нейтронах. Понятие мгновенной критичности реактора является основой для понимания специфической для реакторных установок физической опасности - опасности возникновения неуправляемого разгона мощности реактора при сообщении ему больших положительных реактивностей.
Таким образом, основным принципом, на базе которого формулируется подавляющее большинство требований ядерной безопасности ЯР является:
Ни при каких обстоятельствах реактору не должна сообщаться положительная реактивность, близкая величине доли запаздывающих нейтронов.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
В связи со сказанным становится понятным, какую величину реактивности считать большой, а какую – малой: положительные реактивности, сравнимые по величине с долей выхода запаздывающих нейтронов – это большие ρ; реактивности, меньшие величины β – это малые ρ.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Анализ кинетики ЯР при введении отрицательной реактивности. При анализе переходных процессов при отрицательной реактивности необходимо отметить, что в этом случае ρ по-прежнему меньше β. Следовательно, для этого случая будут справедливы те же соотношения и закономерности, что и для рассмотренного ранее случая 0 < ρ < β. Необходимо лишь сделать поправки на знак вводимой реактивности. Таким образом, для анализа переходного процесса при отрицательной реактивности можно воспользоваться соотношением (20)
которое для отрицательной реактивности примет вид:
. (33)

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Видно, что у обоих слагаемых в (33) коэффициенты положительны, а экспоненты имеют отрицательные показатели. При этом, как и ранее, первое слагаемое отвечает за установившийся режим, второе – за переходной, т.е. имеют место две стадии развития переходного процесса, свойственные реальным переходным процессам во всех реакторах: стадия начального скачка (в сторону увеличения потока нейтронов) с периодом
. (34)
и стадия чисто экспоненциального спада потока нейтронов с установившимся периодом
. (35)

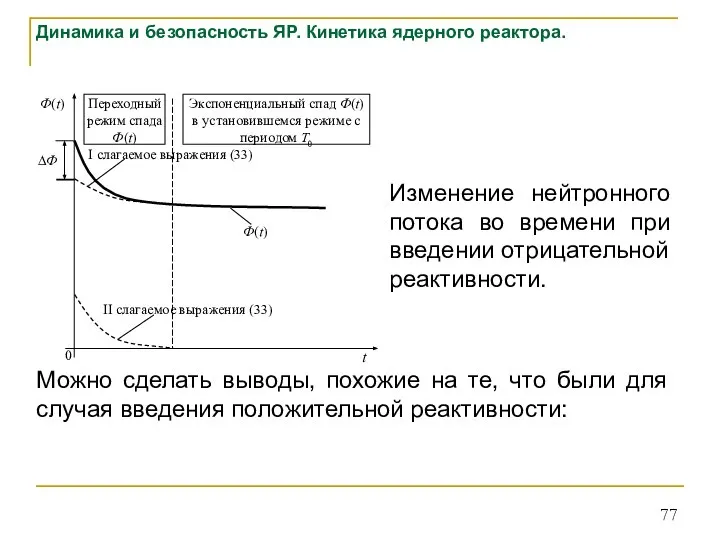
Динамика и безопасность ЯР. Кинетика ядерного реактора.
Изменение нейтронного потока во времени при введении отрицательной реактивности.
Можно сделать выводы, похожие на те, что были для случая введения положительной реактивности:

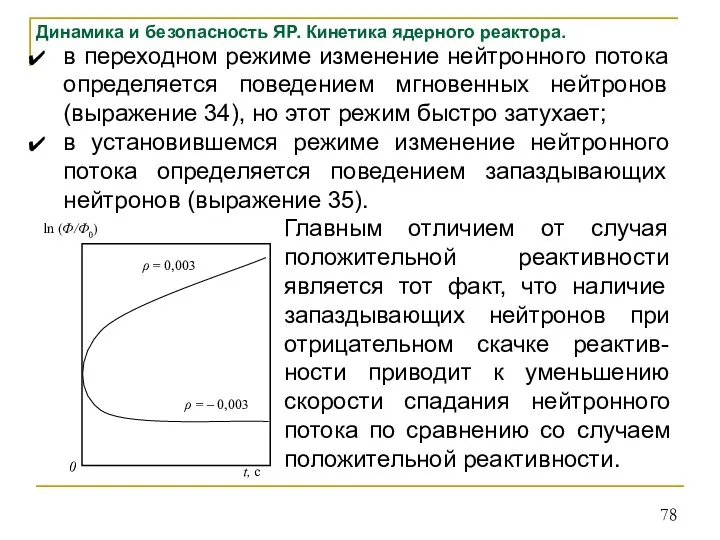
в переходном режиме изменение нейтронного потока определяется поведением мгновенных нейтронов (выражение 34), но этот режим быстро затухает;
в установившемся режиме изменение нейтронного потока определяется поведением запаздывающих нейтронов (выражение 35).
Главным отличием от случая положительной реактивности является тот факт, что наличие запаздывающих нейтронов при отрицательном скачке реактив-ности приводит к уменьшению скорости спадания нейтронного потока по сравнению со случаем положительной реактивности.
Динамика и безопасность ЯР. Кинетика ядерного реактора.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Дадим физическую интерпретацию полученного. При скачкообразном сообщении критическому реактору отрицательной реактивности первыми всегда реагируют на это возмущение мгновенные нейтроны: резко уменьшается скорость их генерации.
И если бы в реакторе не было бы запаздывающих нейтронов, то процесс начального спада Ф(t) происходил бы во много раз быстрее (поскольку время жизни мгновенных нейтронов во много раз меньше времени жизни запаздывающих нейтронов любой группы). То есть это был бы практически безынерционный бросок Ф(t) вниз к остановке ЯР. Но в реакторе есть ЯПЗН, и их стационарные концентрации в критическом реакторе достаточно высоки. Тогда в первые секунды начального скачка достаточно высоки и скорости их β-распада.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Это значит, что вначале высоки и скорости генерации запаздывающих нейтронов всех групп, и получается, что эти добавки запаздывающих нейтронов в общий цикл размножения тормозят общее падение плотности нейтронов Ф(t), которое без них было бы очень резким. Но поскольку с уменьшением Ф(t) синхронно уменьшается и скорость деления ядер топлива, то с той же синхронностью уменьшается и скорость генерации ЯПЗН всех групп. Но при этом скорость уменьшения концентраций ЯПЗН не может быть ниже скорости их β-распада. Это означает, что скорость снижения потока нейтронов не может быть больше, чем скорость β-распада самой долгоживущей группы ЯПЗН.
Реактор (как и автомобиль) мгновенно остановить нельзя!

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Изменение мощности ЯР. В реальных ЯР изменение мощности осуществляется не одним скачком введения реактивности большой величины, а последователь-ностью (ступенями) введения реактивностей малых величин.
Подъем мощности. Пусть ЯР отработал в критическом состояние на мощности P1 достаточно долгое время (сколько?). Возникла необходимость поднять мощность до уровня P2.
На рисунке показаны основные операции, выполняемые с помощью подвижных стержней-поглотителей при подъёме мощности реактора, и переходные процессы P(t), которые следуют в реакторе в ответ на перемещения поглотителей (группа управляющих стержней показана как один стержень).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Оператор производит подъем сте-ржня выше критического положения, введя тем самым положитель-ную реакти-
вность (участок а). Вначале наблюдается небольшой скачок мощности, который затем плавно переходит в экспоненциальное нарастание установившимся периодом.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Для увеличения темпа роста мощности нужно увеличить значение реактивности реактора. Это достигается путём дополнительного перемещения поглотителей вверх (участок б). В ответ на это реактор опять отзывается начальным скачком мощности вверх, переходящим в экспоненциальное нарастание мощности с новым установившимся периодом, благодаря чему рост мощности реактора будет происходить по более крутой экспоненте.
Чтобы не допустить сильного разгона оператор опускает поглотители в предыдущее (надкритическое) положение (участок в). Реактор на это отзовётся начальным скачком мощности вниз, но так как поглотители вернулись в старое надкритическое положение, ЯР после этого скачка вниз будет продолжать более медленный разгон мощности по той же старой экспоненте, по которой шло увеличение мощности на участке (а).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Но скорость увеличения мощности по сравнению с участком (а) на участке (в) стала большей, и необходимо ещё больше снизить темп нарастания мощности. Стержни опускаются ниже (участок г), оставляя их всё же выше критического положения: реактор немедленно отреагирует на это ваше действие скачком мощности вниз, завершающимся переходом на более пологую возрастающую экспоненту, соответствующую более малой величине введенной положительной реактивности. Появляется время понаблюдать, как медленно растёт мощность реактора, приближаясь к нужному уровню P2.
Наконец, мощность реактора достигает требуемого уровня P2. После чего стержни возвращаются в исходное критическое положение (участок д).

Динамика и безопасность ЯР. Кинетика ядерного реактора.
При этом величина мощности реактора небольшим скачком идет вниз и стабилизируется на новом уровне: реактор вновь стал критичным на новом, более высоком, уровне мощности, его реактивность вновь стала равной нулю.
Существенным моментом техники управления реактором при любом сообщении ему положительной реактивности является введение реактивности малыми «порциями», что обеспечивает ядерную безопасность реакторной установки.
Технологический регламент для любой ЯЭУ устанавливает ограничения по величине периода удвоения мощности. Например, для ВВЭР-1000 устанавливается допустимая величина периода удвоения мощности ЯР при положительных реактивностях, равная 100 с.

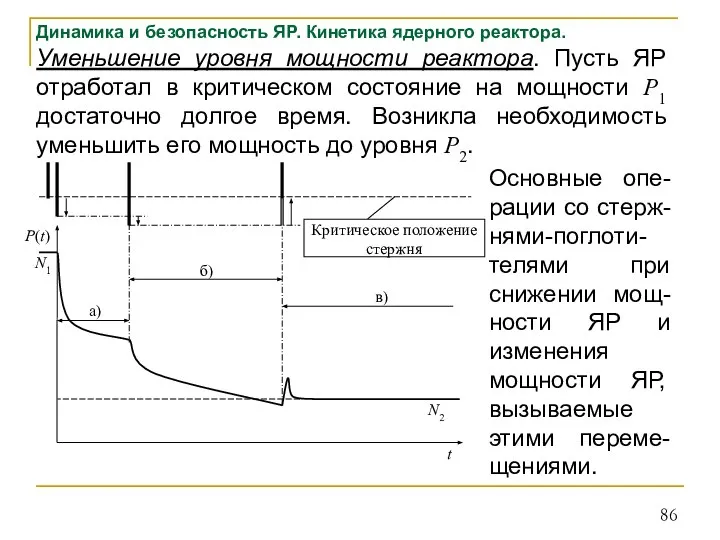
Динамика и безопасность ЯР. Кинетика ядерного реактора.
Уменьшение уровня мощности реактора. Пусть ЯР отработал в критическом состояние на мощности P1 достаточно долгое время. Возникла необходимость уменьшить его мощность до уровня P2.
Основные опе-рации со стерж-нями-поглоти-телями при снижении мощ-ности ЯР и изменения мощности ЯР, вызываемые этими переме-щениями.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Эффективная доля запаздывающих нейтронов.*
Во всех полученных соотношениях кинетики ЯР, строго говоря, нужно использовать не β или βi, а βэф или βэфi.
Например, уравнение обратных часов должно иметь вид:
* Вопрос об эффективной доле запаздывающих нейтронов рассмотреть самостоятельно.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
1.5. Единицы измерения реактивности.
Реактивность - величина абсолютно безразмерная. То есть, во-первых, реактивность может измеряться в безразмерных долях от единицы, например, ρ = 0,0016 или ρ = 0,0005. Часто эти доли от единицы называют абсолютными единицами реактивности (а.е.р.).
Поскольку при управлении реактором операторы имеют дело с небольшими величинами реактивности, в ходу другая единица реактивности, численно в 1000 раз большая, чем 1 а.е.р., а потому называемая тысячной долей ρ (т.д.). 1 т.д. = 10-3 а.е.р.
Иногда используется единица стотысячная доля (с.т.д.) (за рубежом она обозначается pcm):
1 с.т.д. (psm) = 10-5 а.е.р.= 10-2 т.д.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Как всякую относительную величину, ρ можно выразить в процентах: ρ = (±∆kэф/kэф) ·100%.
1 т.д. = 10–3 = 0,1%.
Другим способом измерения реактивности измерение в обратных часах (о.ч.). Реактивность 1 о.ч. – это реактивность реактора, имеющего установившийся период, равный 1 часу (3600 с):
.
Величина обратного часа зависит от вида топлива. Так, для топлива из U235 1о.ч. = 2,5 · 10-5 а.е.р. = 2,5 · 10-3%.
В настоящее время единицы о.ч. и с.т.д. применяются очень редко.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Ранее мы установили, что критерием управляемости ЯР является условие (см. «Мгновенная критичность реактора) ρ = β или, что более правильно, ρ = βэф.
В связи с этим величина реактивности реактора, численно равная эффективной доле запаздывающих нейтронов в нём, может служить в качестве естественной и удобной единицы измерения реактивности для любых реакторов.
В отечественной практике эта единица так и называется доля от βэф (например, «реактивность равна 0,15 βэф ») Американцы дали этой единице своё название - доллар, а сотой части этой единицы - цент. То есть по-американски упомянутая величина реактивности звучит как “0,15 доллара” (или «15 центов») и пишется кратко ρ = 0.15$ или ρ = 15 с.
ρ ($) = ρ (а.е.р.) / βэф.

Динамика и безопасность ЯР. Кинетика ядерного реактора.
Ввиду важности вопроса обеспечения ядерной безопасности выражение реактивности в $ (долях βэф) удобно, т.к. такое выражение ρ позволяет судить о степени приближения (удаления) от неупраляемого состояния реактора, причем независимо от типа ЯР и вида его топлива. Таким образом, выражение ρ в $ (долях βэф) является универсальной единицей.
На отечественных реакторах встречается измерение реактивности в линейных сантиметрах перемещения регулирующих стержней. Например, для первой АЭС (г. Обнинск) перемещение регулятора на 10 см эквивалентно изменению реактивности на 4,5·10-4 а.е.р. Для каждого реактора эта величина различна, поэтому ее использование в широком масштабе нецелесообразно.