Содержание
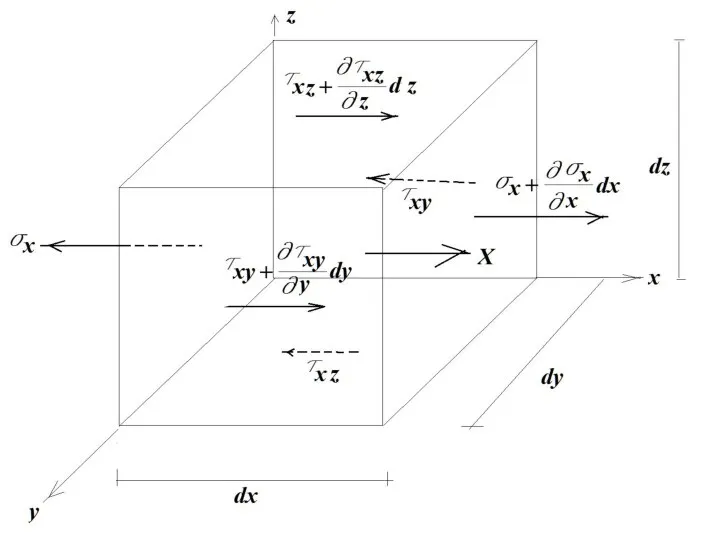
- 2. Теория напряжений является общей для всех разделов механики сплошной среды: теории упругости, теории пластичности и теории
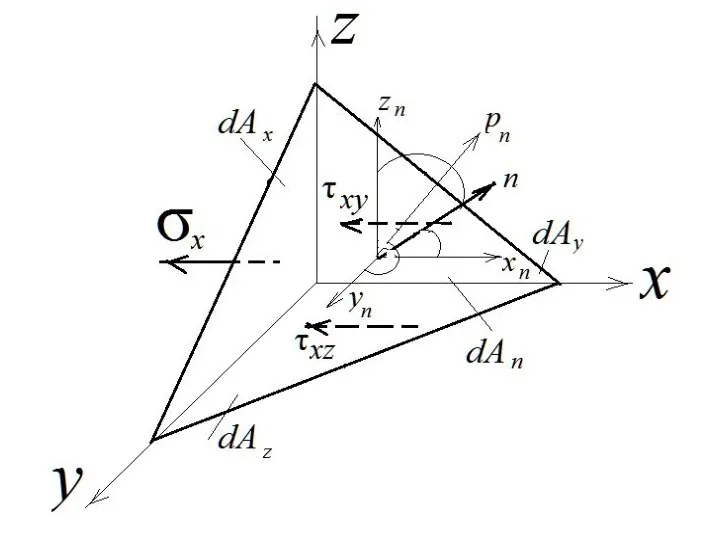
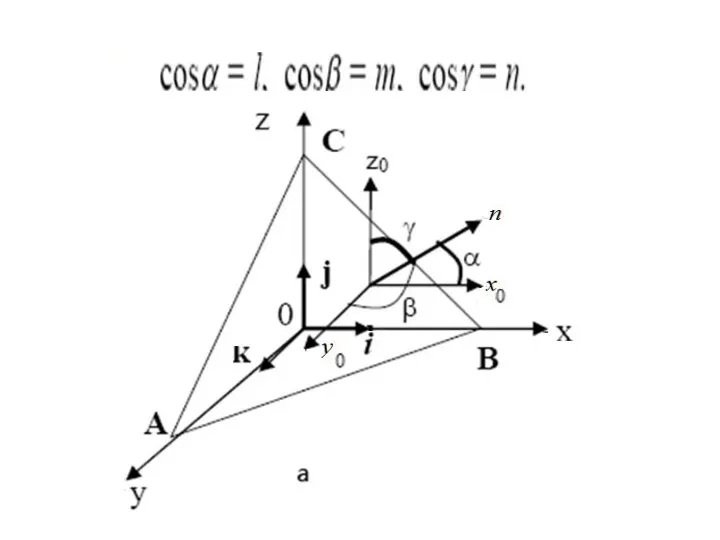
- 9. Напряжения на наклонных площадках. Условия на поверхности
- 13. Эти уравнения используются в двух целях: 1.для определения напряжений на наклонных площадках, т.е. для установления напряженного
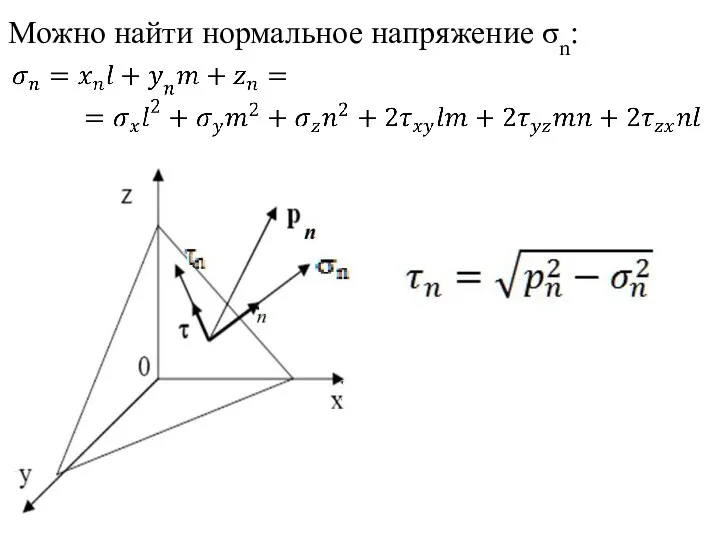
- 14. Можно найти нормальное напряжение σn:
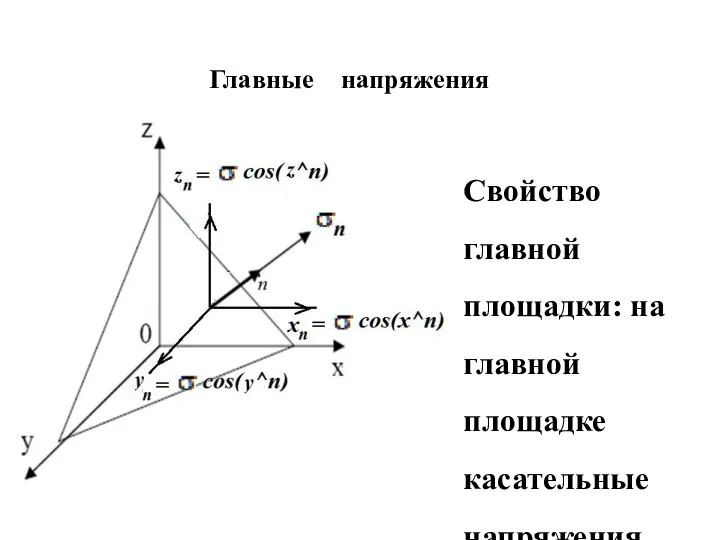
- 15. Главные напряжения Свойство главной площадки: на главной площадке касательные напряжения равны нулю.
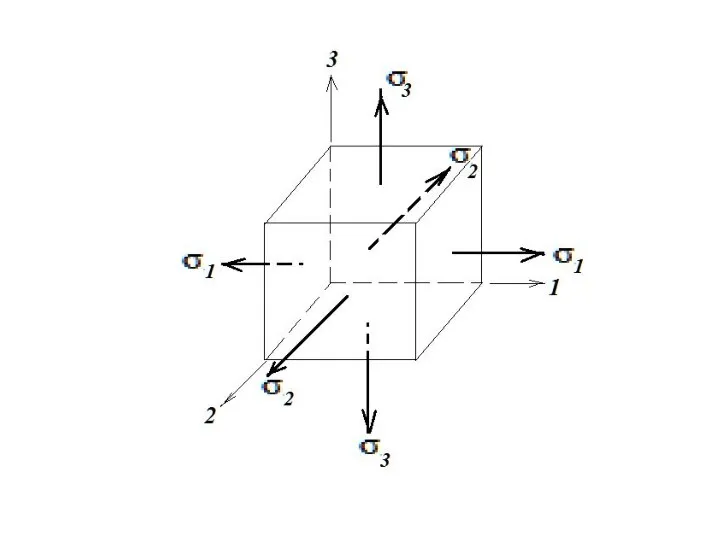
- 16. Предположим, что наклонная площадка является главной. Тогда вектор полного напряжения pn будет совпадать с нормалью к
- 17. Xn= σxcos(n^x)+ τxycos(n^y)+ τxzcos(n^z) Так как Xn=σcos(n^x), получим: (σx-σ)cos(n^x)+ τxycos(n^y)+ τxzcos(n^z)=0. Рассуждая аналогично можно получить следующую
- 26. Скачать презентацию







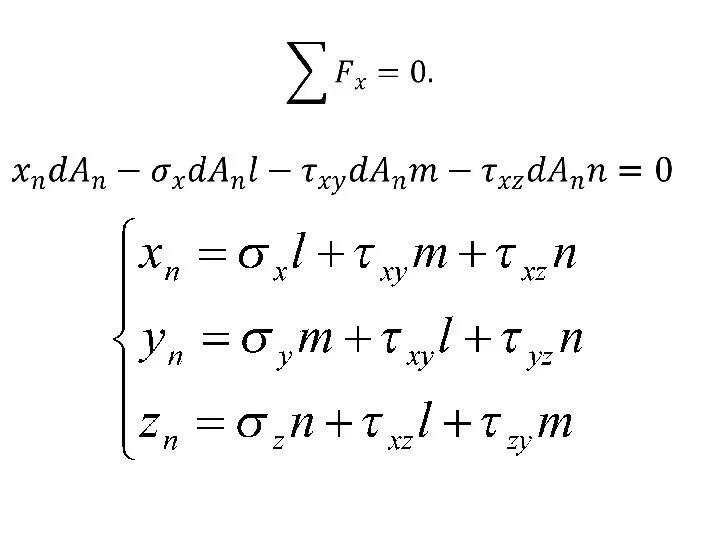









 Презентация по физике "Механика.Система отсчета.Путь и перемещение.Средняя скорость" -
Презентация по физике "Механика.Система отсчета.Путь и перемещение.Средняя скорость" -  Определение скорости движения условной лодки по силе сопротивления при работе на тренажере
Определение скорости движения условной лодки по силе сопротивления при работе на тренажере Вес тела. Невесомость
Вес тела. Невесомость Слайды по физике
Слайды по физике Естественный способ задания движения
Естественный способ задания движения Техническое обслуживание масляного выключателя ВМП-10к
Техническое обслуживание масляного выключателя ВМП-10к Графическое представление движения
Графическое представление движения Сила. Сила тяжести
Сила. Сила тяжести Электронный нос или что может заменить нос собаки
Электронный нос или что может заменить нос собаки Электрические явления. Решение задач
Электрические явления. Решение задач ВКР: Расчет, изготовление и исследование амплитудной цилиндрической линзы
ВКР: Расчет, изготовление и исследование амплитудной цилиндрической линзы Идеальный газ в молекулярно-кинетической теории
Идеальный газ в молекулярно-кинетической теории Динамика поступательного движения. Лекция 3
Динамика поступательного движения. Лекция 3 Оптимальное проектирование диска компрессора
Оптимальное проектирование диска компрессора Работа и мощность постоянного тока
Работа и мощность постоянного тока Регулирование с воздействием по возмущению
Регулирование с воздействием по возмущению Переходные процессы в ЭЦ
Переходные процессы в ЭЦ Презентация на тему Индукция магнитного поля (9 класс)
Презентация на тему Индукция магнитного поля (9 класс)  Расчёт расхода электроэнергии
Расчёт расхода электроэнергии Смысловое чтение и работа с текстом на уроках физики в условиях введения в ФГОС
Смысловое чтение и работа с текстом на уроках физики в условиях введения в ФГОС Атомная и ядерная физика
Атомная и ядерная физика Проектирование космического аппарата для посадки на космическое тело с малым гравитационным полем
Проектирование космического аппарата для посадки на космическое тело с малым гравитационным полем Кручение
Кручение КПД нагревателя
КПД нагревателя Плазмохімічне одержання сполук заліза. Магістерська робота
Плазмохімічне одержання сполук заліза. Магістерська робота Физические величины и их измерение
Физические величины и их измерение Расчет режимов резания
Расчет режимов резания Занимательные физические опыты из подручных материалов
Занимательные физические опыты из подручных материалов