Динамика. Лекция 2

Динамика
Масса
Гравитационная и инертная массы равны друг другу
инертная
гравитационная
III закон Ньютона
закон всемирного тяготения

Динамика
Инертная масса – коэффициент пропорциональности между действующей на тело силой и ускорением тела.
Способ определения инертной массы:
Масса – мера инертности.

Динамика
Гравитационная масса – источник гравитационного поля, приводит к взаимному притяжению тел. Определяется законом всемирного тяготения Ньютона.
Способ определения гравитационной массы:
Сравнение сил тяжести эталонного и неизвестного тела
- мера энергии

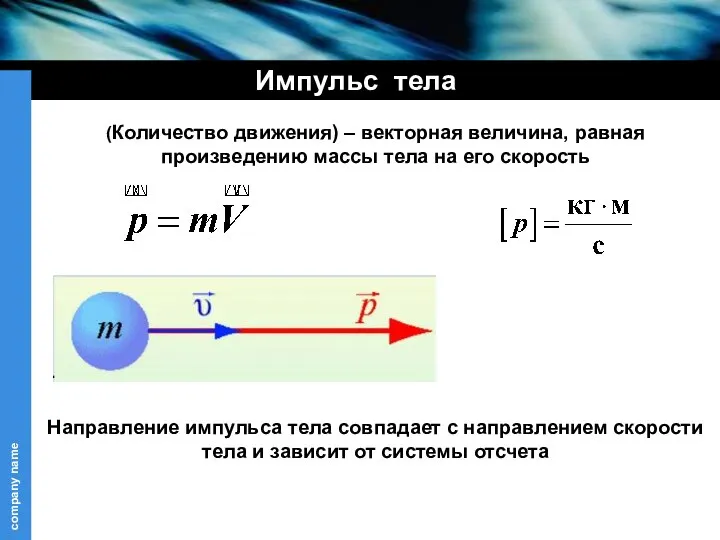
(Количество движения) – векторная величина, равная произведению массы тела на его скорость
Импульс тела
Направление импульса тела совпадает с направлением скорости тела и зависит от системы отсчета

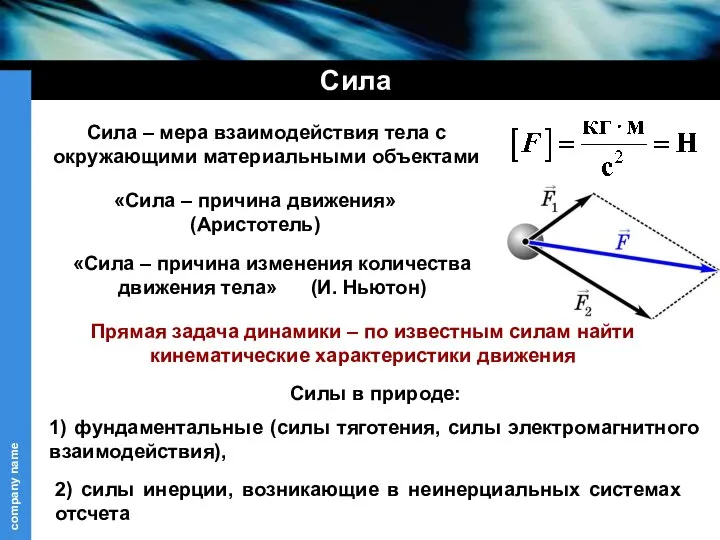
Сила – мера взаимодействия тела с окружающими материальными объектами
Сила
Силы в природе:
«Сила – причина движения» (Аристотель)
«Сила – причина изменения количества движения тела» (И. Ньютон)
Прямая задача динамики – по известным силам найти кинематические характеристики движения
1) фундаментальные (силы тяготения, силы электромагнитного взаимодействия),
2) силы инерции, возникающие в неинерциальных системах отсчета

Сила
Силы в природе:
3) молекулярные силы (силы Ван-дер-Ваальса) – силы взаимодействия молекул и атомов
4) силы, возникающие только при непосредственном взаимодействии тел (силы трения, упругие силы)
5) консервативные и неконсервативные силы
Если работа, совершаемая над телом, не зависит от пути, а определяется только начальным и конечным положениями тела в пространстве, то поле сил называется потенциальным, а сами силы – консервативными (потенциальными).
Силы, работа которых зависит от формы пути, по которому тело переходит из одного положения в другое, называются неконсервативными (диссипативными).

«Математические начала натуральной философии»
(1687г.) Исаак Ньютон
Основа классической механики – законы Ньютона
Законы Ньютона
Первый закон Ньютона (закон инерции)
Второй закон Ньютона
(основное уравнение динамики поступательного движения)
Третий закон Ньютона
(закон взаимности действия)
Механика – классическая, квантовая, релятивистская

Первый закон Ньютона (закон инерции): всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.
1 закон Ньютона
Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета.
Тело, не поддерживаемое внешними воздействиями называется свободным.
Свойство свободных тел сохранять состояние покоя или равномерного прямолинейного движения называется инертностью (инерцией).

1 закон Ньютона
Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно.
Пример ИСО: гелиоцентрическая (звездная) система

Все механические явления в различных инерциальных системах протекают одинаково, т.е. никакими механическими опытами, проводимыми «внутри» данной инерциальной системы, невозможно установить, покоится данная СО или движется прямолинейно и равномерно.
Принцип относительности Галилея
Все инерциальные системы отсчета абсолютно равноправны
Все механические процессы протекают одинаково во всех ИСО
Все системы отсчета, которые относительно инерциальной движутся равномерно и прямолинейно, также являются инерциальными. Систему, движущуюся ускоренно относительно инерциальной, называют неинерциальной.

или
- уравнение движения материальной точки
2 закон Ньютона
Второй закон Ньютона (основной закон динамики поступательного движения) - ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей силе и обратно пропорционально массе тела.
- импульс силы

2 закон Ньютона
- изменение импульса материальной точки равно импульсу силы
если
то
если
то

3 закон Ньютона
Третий закон Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
F12 - сила, действующая на первую материальную точку со стороны второй;
F21 - сила, действующая на вторую материальную точку со стороны первой.
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

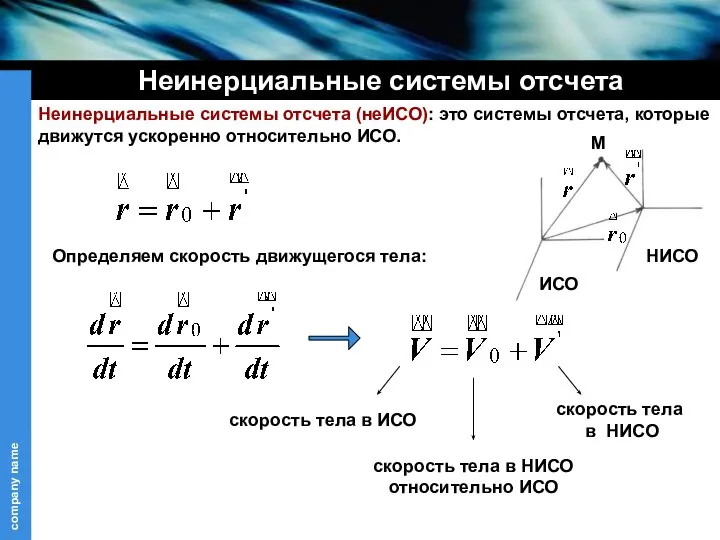
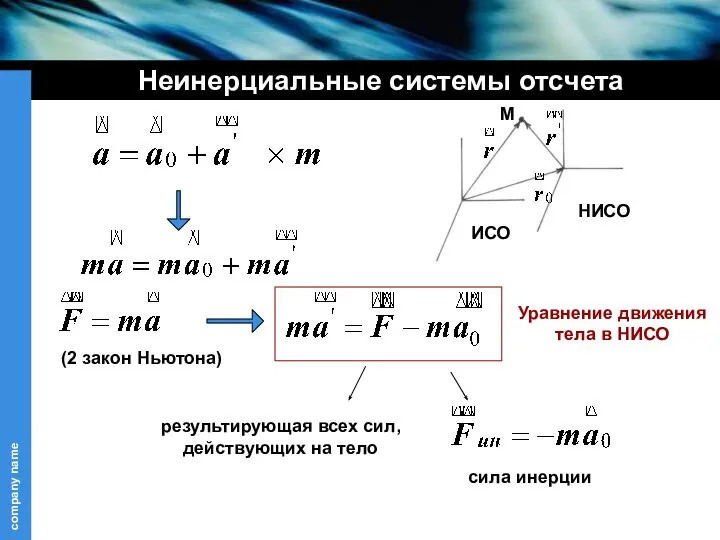
Неинерциальные системы отсчета
Неинерциальные системы отсчета (неИСО): это системы отсчета, которые движутся ускоренно относительно ИСО.
Определяем скорость движущегося тела:
скорость тела в ИСО
скорость тела в НИСО относительно ИСО
скорость тела
в НИСО
ИСО
НИСО
М

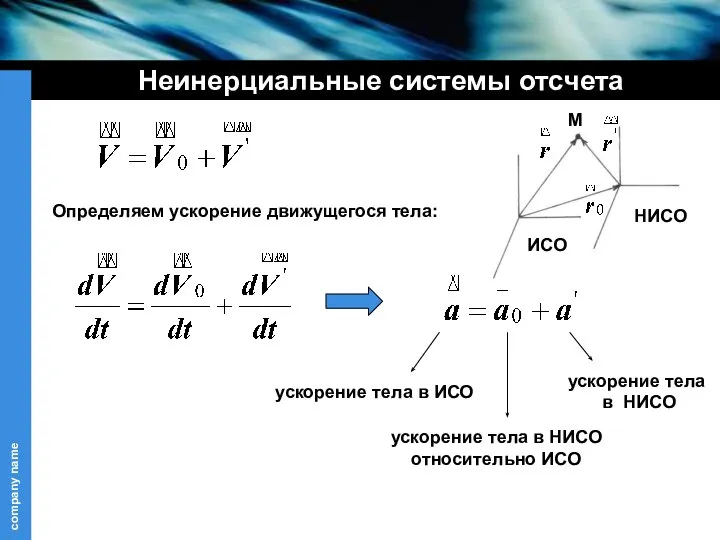
Неинерциальные системы отсчета
Определяем ускорение движущегося тела:
ускорение тела в ИСО
ускорение тела в НИСО относительно ИСО
ускорение тела
в НИСО
ИСО
НИСО
М

Неинерциальные системы отсчета
(2 закон Ньютона)
Уравнение движения
тела в НИСО
результирующая всех сил, действующих на тело
сила инерции
ИСО
НИСО
М

Неинерциальные системы отсчета
Свойства сил инерции:
сила инерции возникает не из-за взаимодействия тел, а лишь вследствие ускоренного движения системы отсчета;
силы инерции зависят от выбора системы отсчета;
силы инерции не подчиняются 3 закону Ньютона;
силы инерции пропорциональны массе тела.

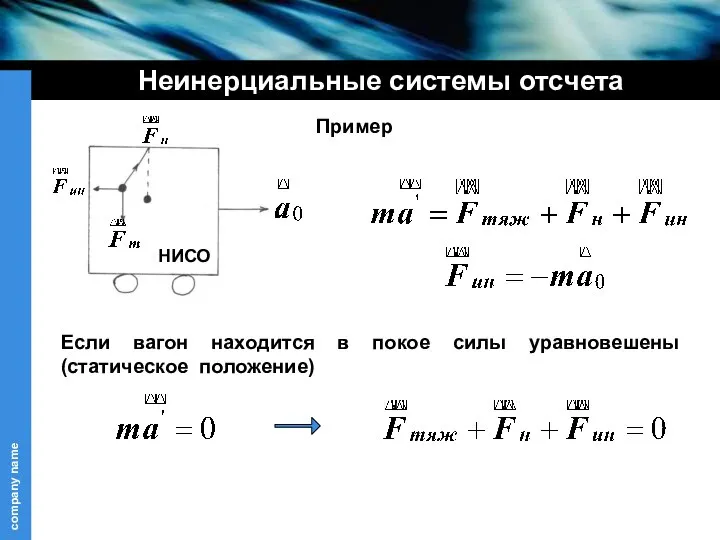
Неинерциальные системы отсчета
Пример
Если вагон находится в покое силы уравновешены (статическое положение)
НИСО

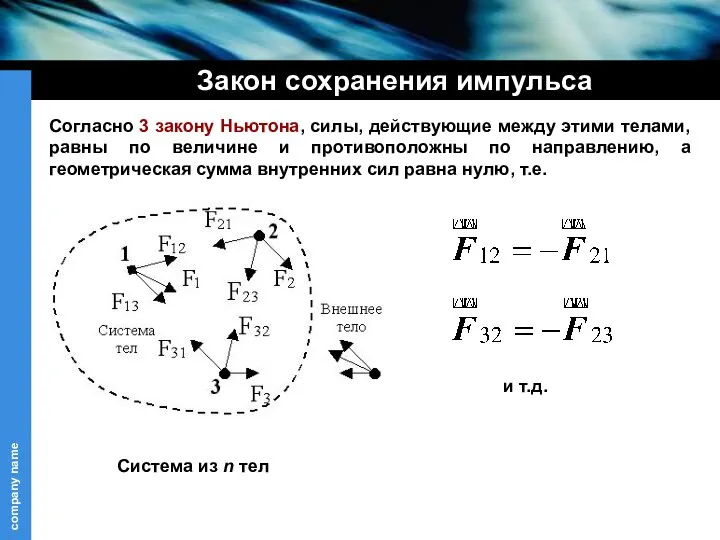
Закон сохранения импульса
Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой.
Силы взаимодействия между материальными точками механической системы называются внутренними.
Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними.
Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной).

Закон сохранения импульса
- внутренние силы, действующие на 1-ое тело
со стороны 2-го, 3-го и т.д.
- внешние силы, действующие на 1-ое, 2-ое тело и т.д.
Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых равны

Закон сохранения импульса
Согласно 3 закону Ньютона, силы, действующие между этими телами, равны по величине и противоположны по направлению, а геометрическая сумма внутренних сил равна нулю, т.е.
и т.д.
Система из n тел

Закон сохранения импульса
Запишем уравнения динамики движения материальных точек системы, согласно 2 закону Ньютона:

Закон сохранения импульса
сумма импульса системы мат. точек называется импульсом системы материальных точек
импульс одной
материальной точки
по 3 закону Ньютона

Закон сохранения импульса
Скорость изменения импульса системы материальных точек равна сумме внешних сил, действующих на точки системы.

Закон сохранения импульса
Скорость изменения импульса системы материальных точек равна сумме внешних сил, действующих на точки системы.
Импульс замкнутой системы сохраняется,
т.е. не изменяется с течением времени.
В случае отсутствия внешних сил:

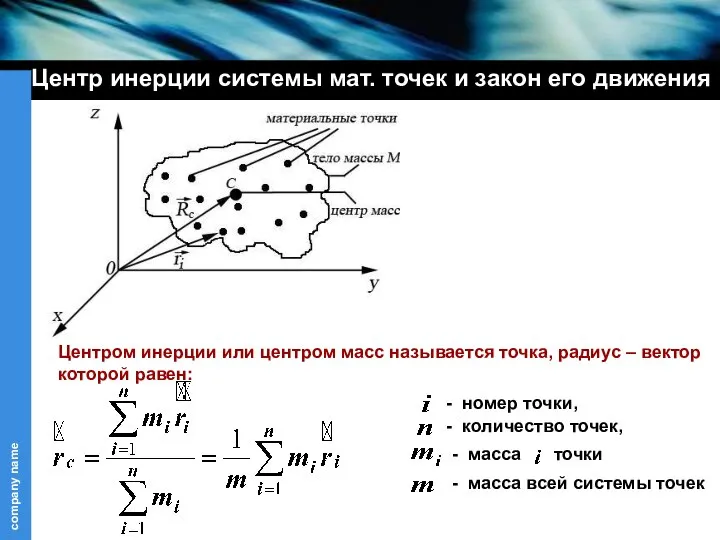
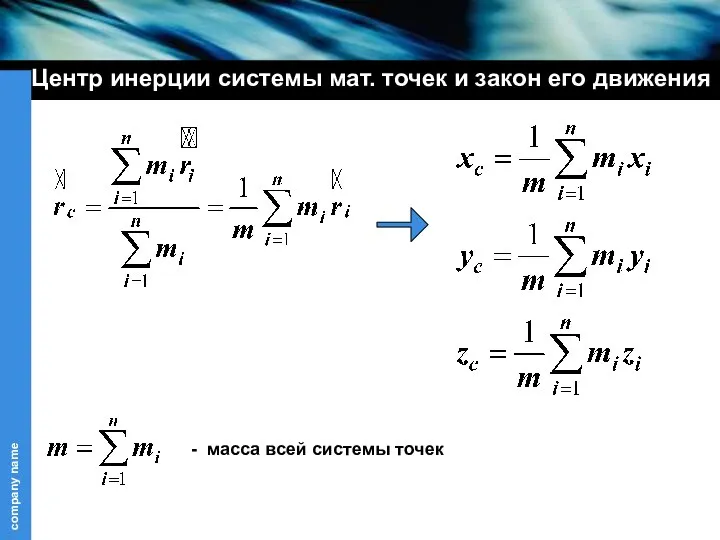
Центр инерции системы мат. точек и закон его движения
Центром инерции или центром масс называется точка, радиус – вектор которой равен:
- номер точки,
- количество точек,
- масса
точки
- масса всей системы точек

Центр инерции системы мат. точек и закон его движения
- масса всей системы точек

Центр инерции системы мат. точек и закон его движения
Скорость центра инерции системы материальных точек
Импульс системы материальных точек равен произведению масс всей системы на скорость ее центра инерции

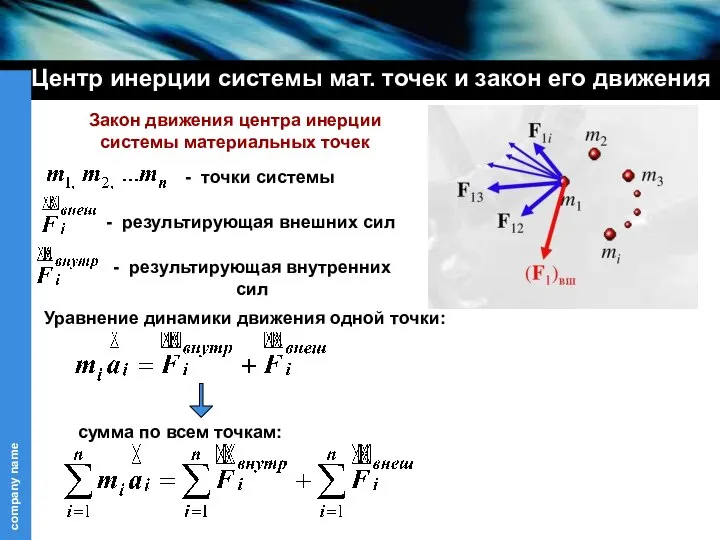
Центр инерции системы мат. точек и закон его движения
Закон движения центра инерции системы материальных точек
- точки системы
- результирующая внешних сил
- результирующая внутренних сил
Уравнение динамики движения одной точки:
сумма по всем точкам:

Центр инерции системы мат. точек и закон его движения
масса системы
ускорение центра масс

Центр инерции системы мат. точек и закон его движения
Если
Закон движения центра масс системы материальных точек
т.к.
Центр масс системы материальных точек движется как материальная точка, масса которой равна массе всей системы, и на которую действует сила, равная результирующей всех внешних сил, приложенных к системе.

Центр инерции системы мат. точек и закон его движения
Основное уравнение динамики поступательного движения твердого тела
Твердое тело можно рассматривать как систему материальных точек, поэтому полученное уравнение называют основным уравнением динамики поступательного движения твердого тела.
Следствия:
закон сохранения импульса
1)