Сложное движение точки

Учебный курс разработан на кафедре ФН3 "Теоретическая механика" МГТУ им. Н.Э. Баумана
Переносным движением для точки М называется движение вместе с подвижной системой, т.е. движение местоположения точки М в подвижной системе Оxyz вместе с ней относительно неподвижной О1XYZ.

Формула Бура
МГТУ им. Н.Э. Баумана
В подвижной системе отсчета Oxyz :
Продифференцируем это выражение по времени:
Первые три слагаемые учитывают изменение вектора при неизменных ортах
– формулы Пуассона.
– формула Бура.
Полная (абсолютная) производная произвольного вектора, равна сумме локальной производной этого вектора и векторного произведения угловой скорости подвижной системы отсчёта на дифференцируемый вектор.

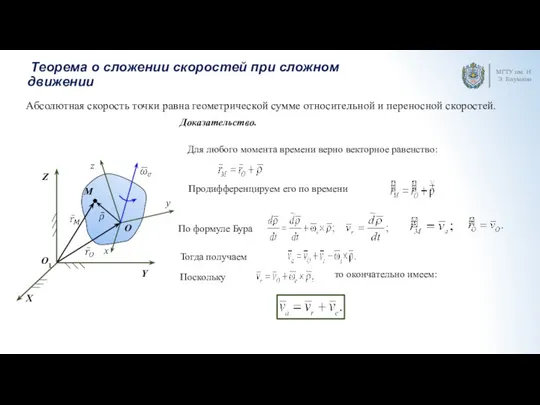
Теорема о сложении скоростей при сложном движении
МГТУ им. Н.Э. Баумана
Для любого момента времени верно векторное равенство:
Продифференцируем его по времени
Абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.
Доказательство.
По формуле Бура
Тогда получаем
Поскольку
то окончательно имеем:

Теорема о сложении ускорений при сложном движении
МГТУ им. Н.Э. Баумана
Кинематическая теорема Кориолиса. Абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса.
Док-во: по теореме о сложении скоростей, абсолютная скорость точки
Продифференцируем по времени
Воспользовавшись формулой Бура, получим
Здесь
– переносное ускорение,
– ускорение Кориолиса.
Окончательно
– кинематическая теорема Кориолиса.

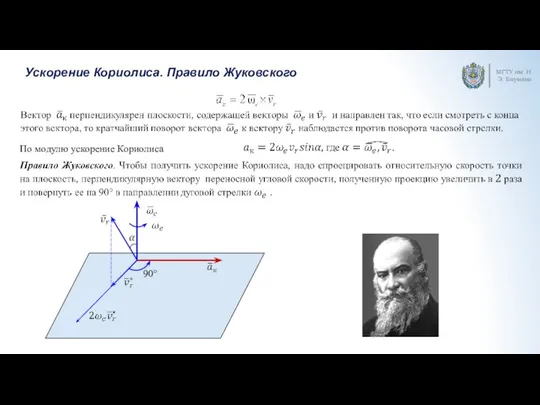
Ускорение Кориолиса. Правило Жуковского
МГТУ им. Н.Э. Баумана
По модулю ускорение Кориолиса
90°

Нули ускорения Кориолиса.
МГТУ им. Н.Э. Баумана
1. Переносное движение – поступательное, ωе= 0
Рассмотрим случаи, когда ускорение Кориолиса обращается в нуль.

Пример
МГТУ им. Н.Э. Баумана
Решение.
Свяжем подвижную систему координат с Землей. Тогда:
переносное движение – (вместе с вращающейся Землей) - по окружности радиуса h (расстояние до оси вращения Земли).
Относительная траектория – окружность радиуса R.
Относительная траектория
По теореме о сложении скоростей:
Относительная скорость
Переносная скорость направлена по касательной к параллели и равна:
Поскольку переносная и относительная скорости ортогональны, то: