Движение частиц в экспериментах ЯМР

Пространственная зависимость вводится градиентом магнитного поля
Макроскопическое движение
Уравнения Блоха-Торри (диффузия)
Квантовая радиофизика
Движение частиц в экспериментах ЯМР

Диффузия в ЯМР

Решение уравнений Блоха-Торри для одномерной изотропной диффузии
В терминах эффективного градиента
Квантовая радиофизика
Диффузия в ЯМР

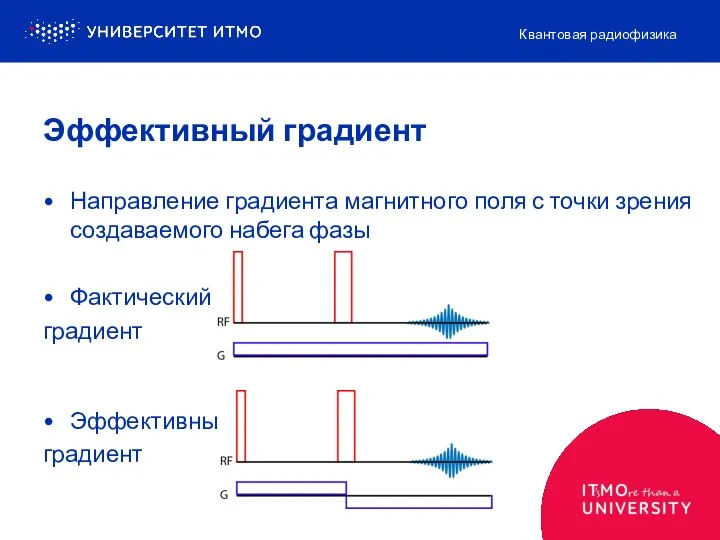
Направление градиента магнитного поля с точки зрения создаваемого набега фазы
Фактический
градиент
Эффективный
градиент
Квантовая радиофизика
Эффективный градиент

Диффузная взвешенность вследствие постоянного градиента
Амплитуда сигнала
Квантовая радиофизика
Постоянный градиент

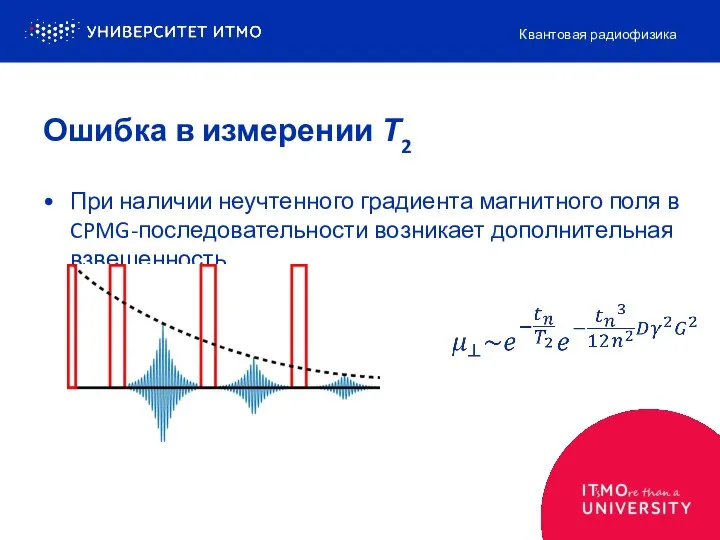
При наличии неучтенного градиента магнитного поля в CPMG-последовательности возникает дополнительная взвешенность
Квантовая радиофизика
Ошибка в измерении Т2

Измерение диффузии методом спинового или стимулированного эха
Амплитуда сигнала
Квантовая радиофизика
Импульсный градиент

2 эксперимента с одинаковыми параметрами τ, Δ, δ, но различной величиной градиента (b2=0, b1=b1)
Квантовая радиофизика
Измерение диффузии

Уравнение Блоха-Торри
Квантовая радиофизика
Анизотропная диффузия

Уравнение Блоха-Торри
Квантовая радиофизика
Анизотропная диффузия

Решение уравнений Блоха-Торри
Квантовая радиофизика
Влияние анизотропной диффузии

b-матрица определяет величину диффузной взвешенности
При наличии эксперимента с bij=0
Квантовая радиофизика
Измерение анизотропной диффузии

Величина сигнала – линейная комбинация из 6 неизвестных переменных
Тогда для, например, 6 измерений с различными направлениями градиентов можно записать
Квантовая радиофизика
Вычисление элементов тензора самодиффузии