Содержание
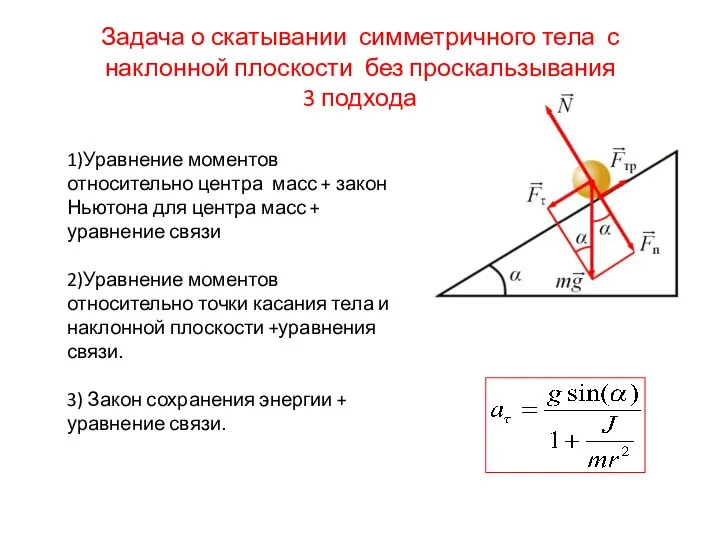
- 2. Задача о скатывании симметричного тела с наклонной плоскости без проскальзывания 3 подхода 1)Уравнение моментов относительно центра
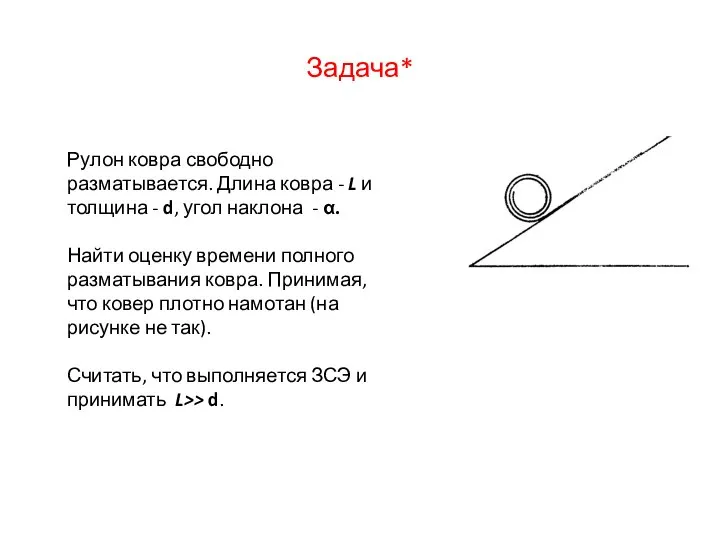
- 3. Задача* Рулон ковра свободно разматывается. Длина ковра - L и толщина - d, угол наклона -
- 4. Расчет момента инерции палочки относительно оси перпендикулярной центру Линейная плотность [кг/м] Момент инерции кусочка Масса кусочка
- 5. Расчет момента инерции диска относительно оси перпендикулярной центру симметрии поверхностная плотность [кг/м2] Момент инерции кольца Масса
- 6. Расчет момента инерции шара относительно оси, проходящей через его центр -плотность [кг/м2] Момент инерции диска: Масса
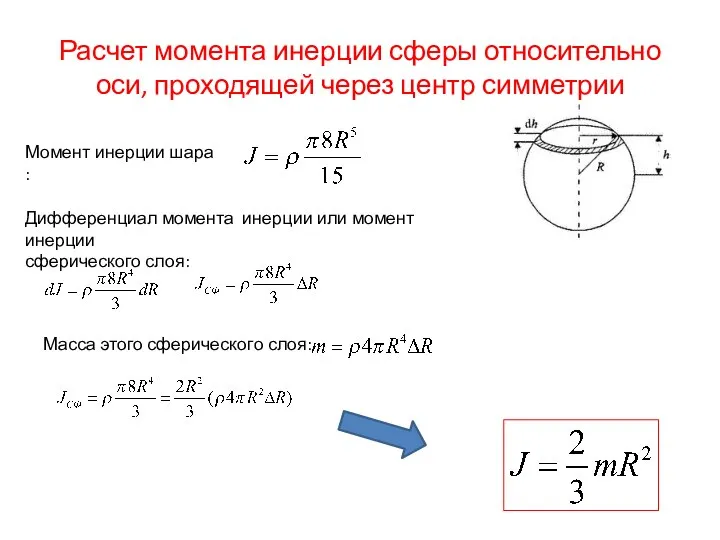
- 7. Расчет момента инерции сферы относительно оси, проходящей через центр симметрии Момент инерции шара : Дифференциал момента
- 8. Уравновешенный гироскоп – быстро вращающееся тело, имеющее три степени свободы
- 9. Прецессия гироскопа* L -момент импульса гороскопа, M - момент внешней силы L -момент импульса гороскопа велик
- 10. Куда катится катушка, которую тянут за нить (проскальзывания нет)? Проекция скорости катушки на нить Уравнение связи
- 11. Диссипативные силы Диссипативные силы – силы, зависящие от скорости, работа которых может приводить к уменьшению общей
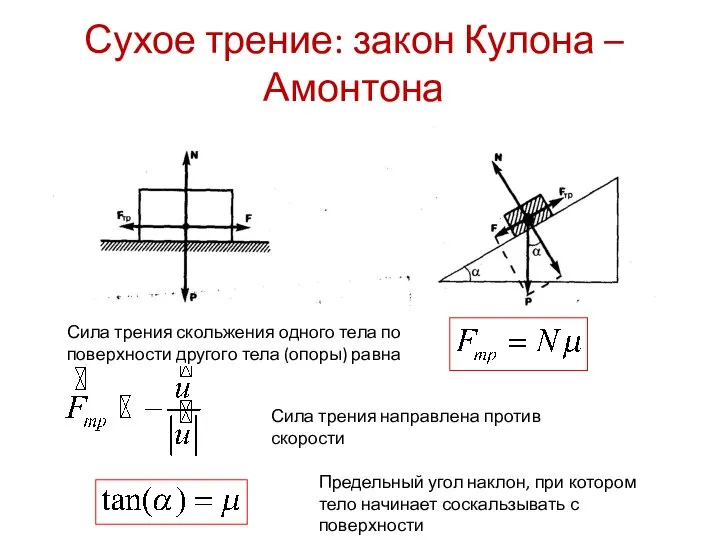
- 12. Сухое трение: закон Кулона –Амонтона Сила трения скольжения одного тела по поверхности другого тела (опоры) равна
- 13. Сухое трение – закон Кулона –Амонтона Теория Эксперимент Таблица: Коэффициенты трения
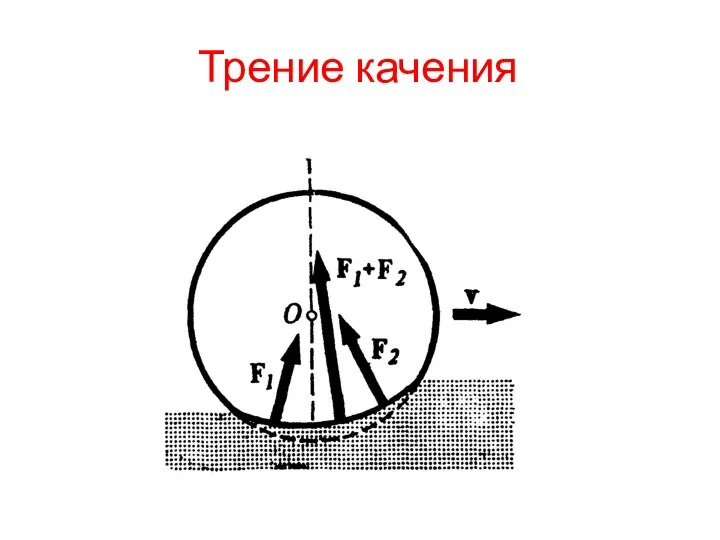
- 14. Трение качения
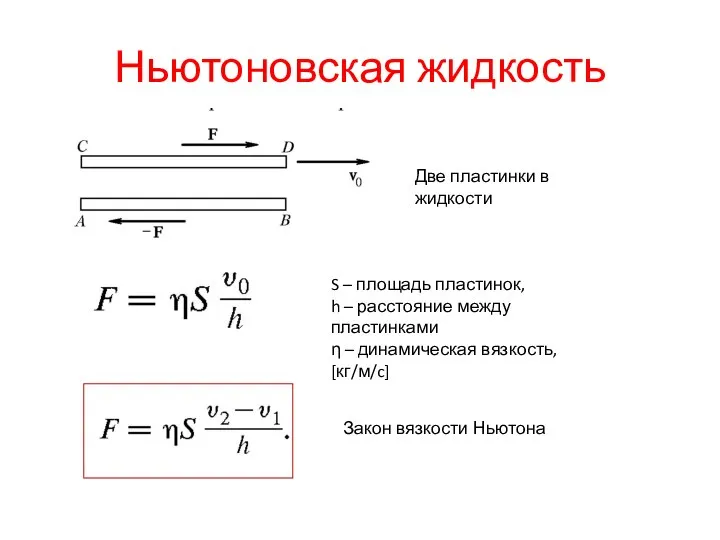
- 15. Ньютоновская жидкость Две пластинки в жидкости S – площадь пластинок, h – расстояние между пластинками η
- 16. Вязкость кинематическая и динамическая η – динамическая вязкость, [кг/м/c] – кинематическая вязкость, [м2/c] Идеальная жидкость –
- 17. Число Рейнольдса l – характерные размеры u – характерная скорость К– кинетическая энергия А– вязкая работа
- 18. Число Рейнольдса l – характерные размеры u – характерная скорость К– кинетическая энергия А– вязкая работа
- 19. Силы сопротивления: низкие скорости Re Точная формула сила трения при обтекании шара Формула Стокса
- 20. Силы сопротивления: высокие скорости Re>>1 доминирует инерционность (NB) Точных решений нет!
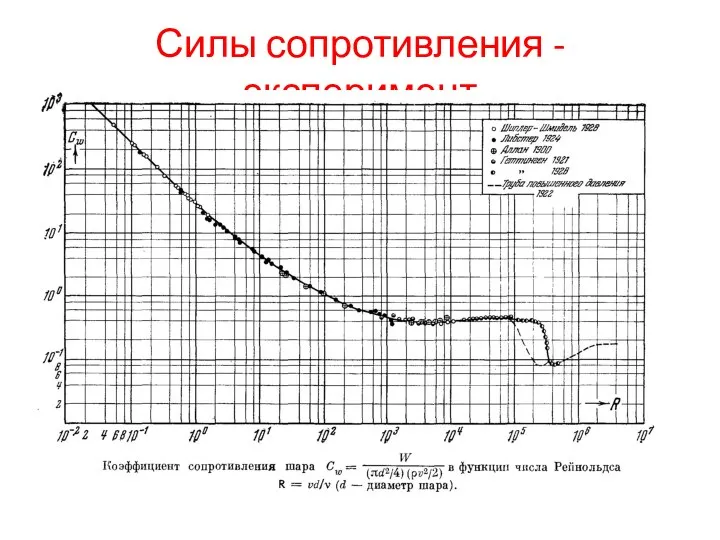
- 21. Силы сопротивления - эксперимент
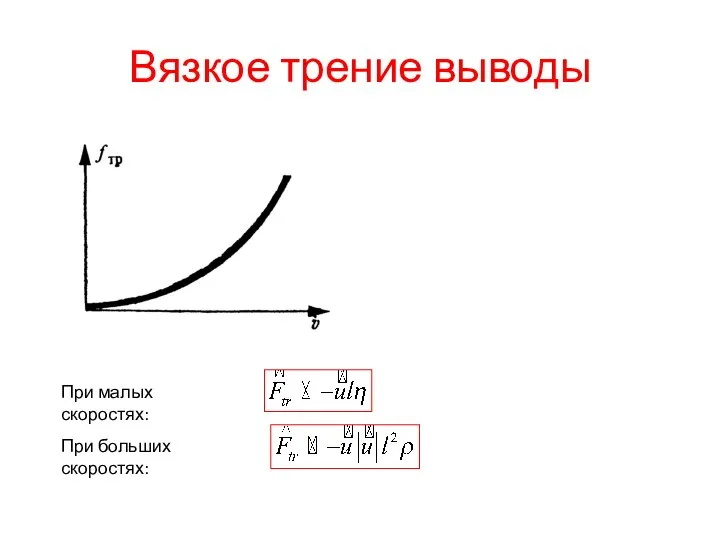
- 22. Вязкое трение выводы При малых скоростях: При больших скоростях:
- 24. Скачать презентацию
![Расчет момента инерции палочки относительно оси перпендикулярной центру Линейная плотность [кг/м] Момент](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1065472/slide-3.jpg)
![Расчет момента инерции диска относительно оси перпендикулярной центру симметрии поверхностная плотность [кг/м2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1065472/slide-4.jpg)
![Расчет момента инерции шара относительно оси, проходящей через его центр -плотность [кг/м2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1065472/slide-5.jpg)





![Вязкость кинематическая и динамическая η – динамическая вязкость, [кг/м/c] – кинематическая вязкость,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1065472/slide-15.jpg)




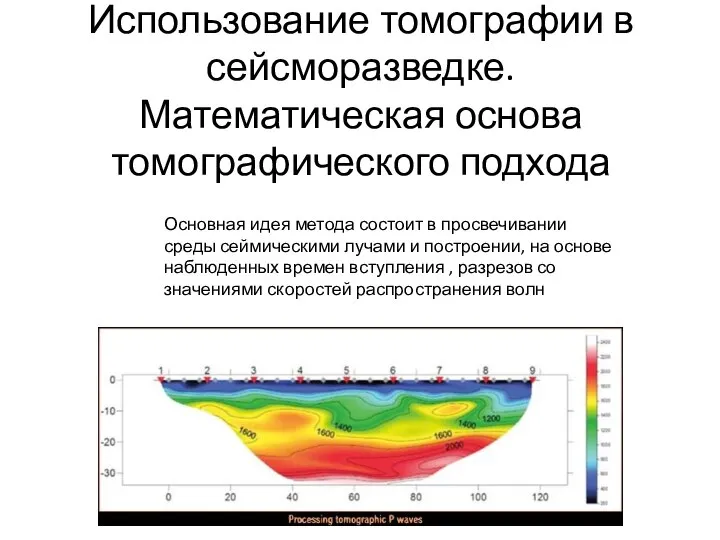 Использование томографии в сейсморазведке. Математическая основа томографического подхода
Использование томографии в сейсморазведке. Математическая основа томографического подхода Работа газа и пара при расширении. Тепловые двигатели
Работа газа и пара при расширении. Тепловые двигатели Решение задач на расчет статически определимых плоских ферм путем построения диаграммы Масквелла-Кремоны
Решение задач на расчет статически определимых плоских ферм путем построения диаграммы Масквелла-Кремоны Свободное падение тел
Свободное падение тел Солнечная энергетика
Солнечная энергетика Презентация на тему Статика
Презентация на тему Статика  svobodnoe_padenie_tel_kopiya
svobodnoe_padenie_tel_kopiya Велотренажёр как альтернативный источник энергии
Велотренажёр как альтернативный источник энергии Курс загальної фізики. Лекція 1. Механічний рух. Кінематика матеріальної точки
Курс загальної фізики. Лекція 1. Механічний рух. Кінематика матеріальної точки Использование электромагнитной индукции
Использование электромагнитной индукции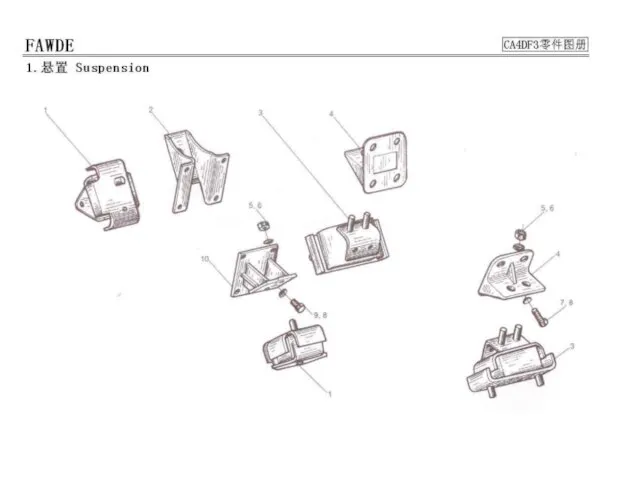 Двигатель FAW CA4DF3
Двигатель FAW CA4DF3 Пара сил и ее действие на тело
Пара сил и ее действие на тело Механические колебания
Механические колебания Закон сохранения импульса
Закон сохранения импульса Кинематика
Кинематика estestvenny_sposob
estestvenny_sposob Телескопи. Типи телескопів за розташуванням
Телескопи. Типи телескопів за розташуванням Дефекты и наноструктурные материалы
Дефекты и наноструктурные материалы Үйкеліс күшін зерттеу
Үйкеліс күшін зерттеу Радиоактивность. Виды радиоактивного облучения
Радиоактивность. Виды радиоактивного облучения Зависимость подвижности электронов от напряженности электрического поля в п/п с многодолинной структурой зоны проводимости
Зависимость подвижности электронов от напряженности электрического поля в п/п с многодолинной структурой зоны проводимости Испарение и конденсация
Испарение и конденсация Смесительный бак с регулированием уровня и температуры. Пример
Смесительный бак с регулированием уровня и температуры. Пример Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Расчет характеристик механического движения. Физика - 7 класс
Расчет характеристик механического движения. Физика - 7 класс Механические свойства горных пород. Напряжения на диаграмме Мора
Механические свойства горных пород. Напряжения на диаграмме Мора Солнечные элементы на основе кристаллического кремния
Солнечные элементы на основе кристаллического кремния О, сколько нам открытий чудных…
О, сколько нам открытий чудных…