Движение в среде с сопротивлением

Природа сил сопротивления
Рассмотрим движение твердого тела в воздушной среде

Природа сил сопротивления
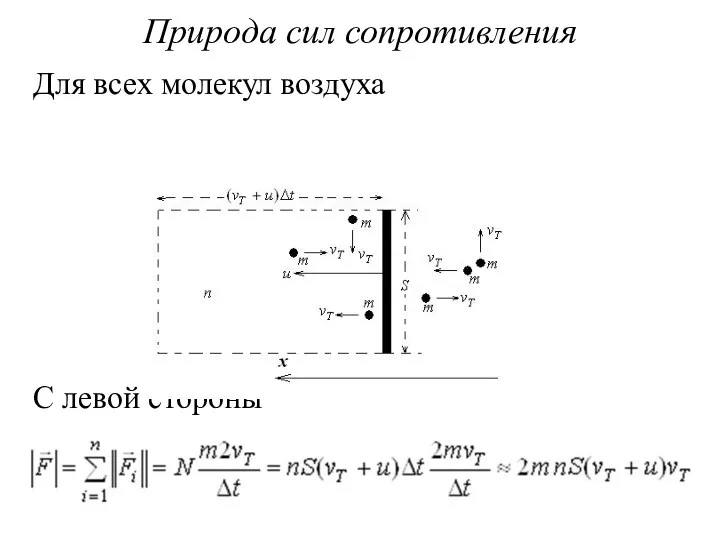
Для всех молекул воздуха
С левой стороны

Природа сил сопротивления
Из условия
При
При

Движение в среде с сопротивлением
Пусть сила сопротивления пропорциональна квадрату скорости

Движение в среде с сопротивлением
Дифференциальное уравнение движения
Либо
Знак «-» – движение вниз (нисходящее движение)
Знак «+» – движение вверх (восходящее движение)

Движение в среде с сопротивлением
Заменим
Тогда дифференциальное уравнение движения
Решение диф. Уравнения зависит от знака, поэтому разобъем решение на две части.

Движение в среде с сопротивлением
Нисходящее движение.
Делим переменные
Интегрируем
Где - постоянная интегрирования

Движение в среде с сопротивлением
Решение уравнения
Делится на 2 случая
А) случай . Ля этого случая
Или

Движение в среде с сопротивлением
Вводим
Следовательно скорость
Используем начальные условия:
Получим

Движение в среде с сопротивлением
Асимптотика поведения:
При поскольку
Константа
Имеет размерность скорости (предельная скорость)

Движение в среде с сопротивлением
Определяем второй интеграл движения
Из уравнения
получаем
Положим при

Движение в среде с сопротивлением
Рассмотрим случай б) при имеем
Или
Либо

Движение в среде с сопротивлением
Определяем постоянную интегрирования

Движение в среде с сопротивлением
Случай 2. Восходящее движение
При подъеме уравнение движения
Делим переменные
И определяем

Движение в среде с сопротивлением
Из условия определяем
Откуда закон изменения скорости

Движение в среде с сопротивлением
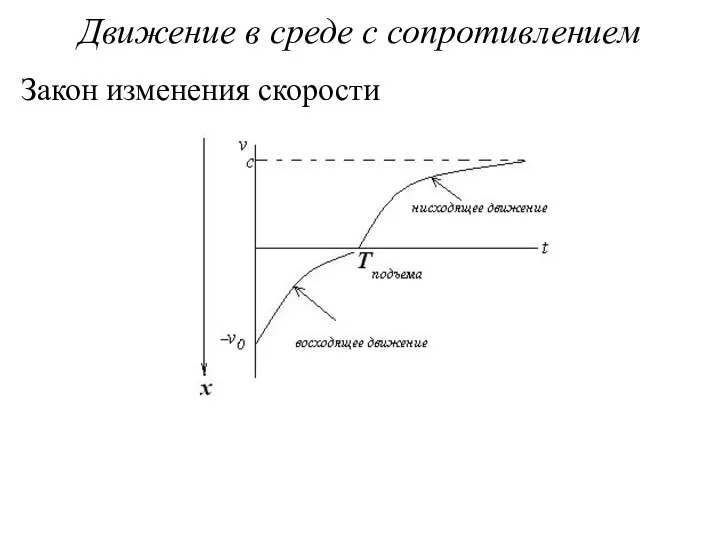
Закон изменения скорости

Движение в среде с сопротивлением
Восходящее движение продолжается до тех пор, пока скорость не обратится в ноль:
Откуда время подъема

Движение в среде с сопротивлением
При этом максимальная высота подъема