Содержание
- 2. Цель рассмотрения системы автоматического управления (САУ) – решение задач анализа синтеза Определить свойства системы с заданными
- 3. Порядок исследования САУ включает Математическое описание системы Исследование в установившемся режиме Исследование в переходном режиме
- 4. Математическое описание – получение математической модели Разбиение системы на звенья По уравнениям и характеристикам отдельных звеньев
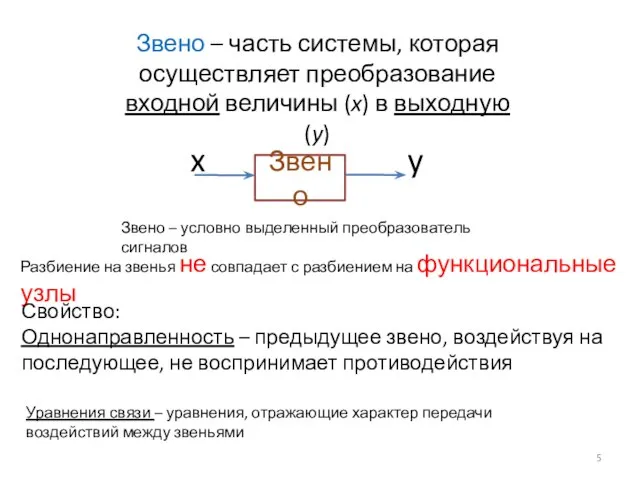
- 5. Звено – часть системы, которая осуществляет преобразование входной величины (x) в выходную (y) Звено x y
- 6. Виды характеристик звеньев Статические Динамические x y f(t)=f=const нелинейная зависимость (в общем случае) Происходит переход звена
- 7. Общее дифференциальное уравнение для звеньев с сосредоточенными параметрами m и n — высший порядок производных от
- 9. Скачать презентацию





 Презентация по физике "Механическое движение" -
Презентация по физике "Механическое движение" -  Презентация на тему Свойства воды
Презентация на тему Свойства воды  Расчет балок по методу начальных параметров. Занятие 8
Расчет балок по методу начальных параметров. Занятие 8 Физическая лихорадка. Методические указания
Физическая лихорадка. Методические указания Механика. Законы сохранения в механике
Механика. Законы сохранения в механике Датчик детонации с подогревом и без подогрева в автомобиле
Датчик детонации с подогревом и без подогрева в автомобиле Тюнинг тормозной системы автомобиля
Тюнинг тормозной системы автомобиля Что явилось причиной движения тела?
Что явилось причиной движения тела? Устройство нанотермометр
Устройство нанотермометр Сенсори температури охолоджувальної рідини
Сенсори температури охолоджувальної рідини Разработка многоканального термометра с обменом данными по радиоканалу
Разработка многоканального термометра с обменом данными по радиоканалу Параллельное программирование для ресурсоёмких задач численного моделирования в физике. Лекция 8
Параллельное программирование для ресурсоёмких задач численного моделирования в физике. Лекция 8 Вектор. Дії над векторами
Вектор. Дії над векторами Принципы радиосвязи и телевидения
Принципы радиосвязи и телевидения Оптика, квантовая и ядерная физика. Лекция 14-15
Оптика, квантовая и ядерная физика. Лекция 14-15 Интерференция, дифракция, поляризация
Интерференция, дифракция, поляризация Деление ядра урана. Устройство и принцип действия ядерного реактора
Деление ядра урана. Устройство и принцип действия ядерного реактора Методы решения задач по динамике материальной точки
Методы решения задач по динамике материальной точки Решение задач. Термодинамика
Решение задач. Термодинамика Постоянный ток
Постоянный ток Сила трения
Сила трения Каковы основные положения молекулярной теории строения вещества?
Каковы основные положения молекулярной теории строения вещества? Презентация на тему Измерительные приборы
Презентация на тему Измерительные приборы  Complex numbers
Complex numbers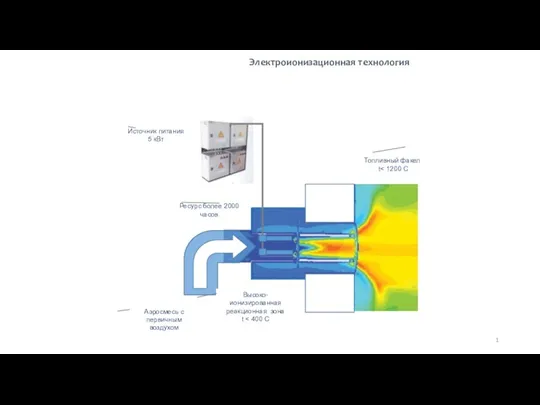 Электроионизационная технология
Электроионизационная технология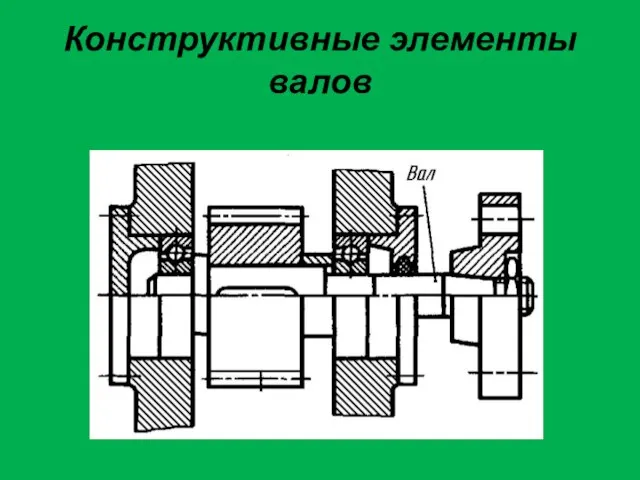 Конструктивные элементы валов
Конструктивные элементы валов Закон Кеплера
Закон Кеплера Матрицы и действия над ними
Матрицы и действия над ними