Содержание
- 2. Центральная и Осевая симметрия Центральная Осевая М О М а
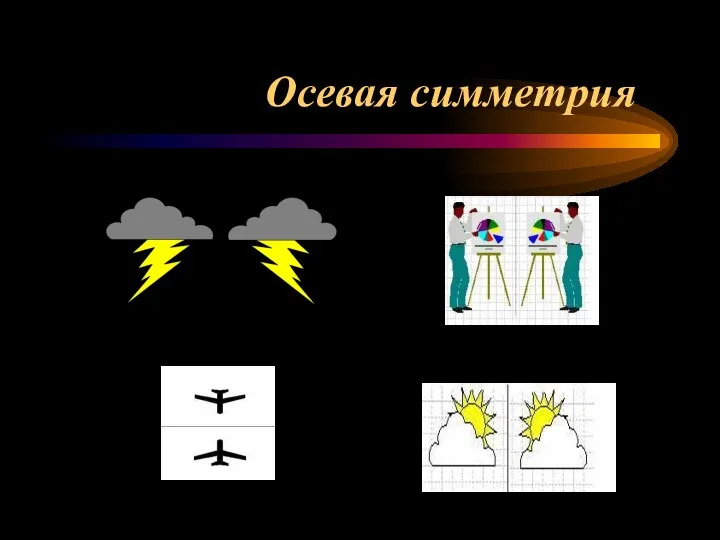
- 3. Осевая симметрия
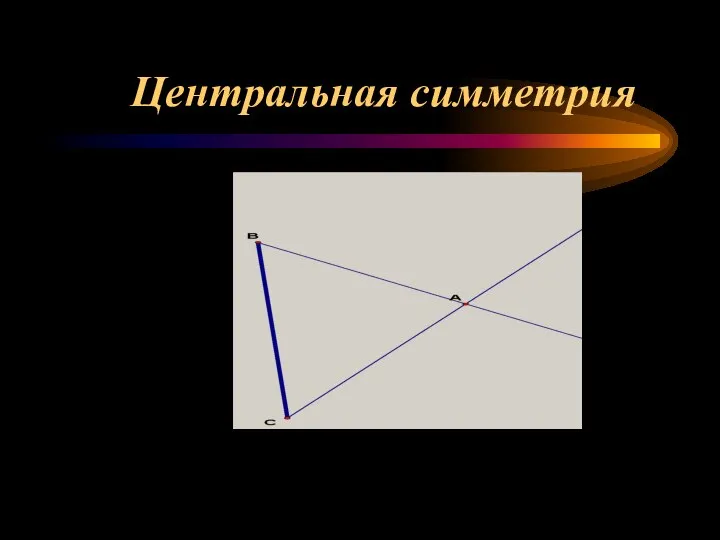
- 4. Центральная симметрия
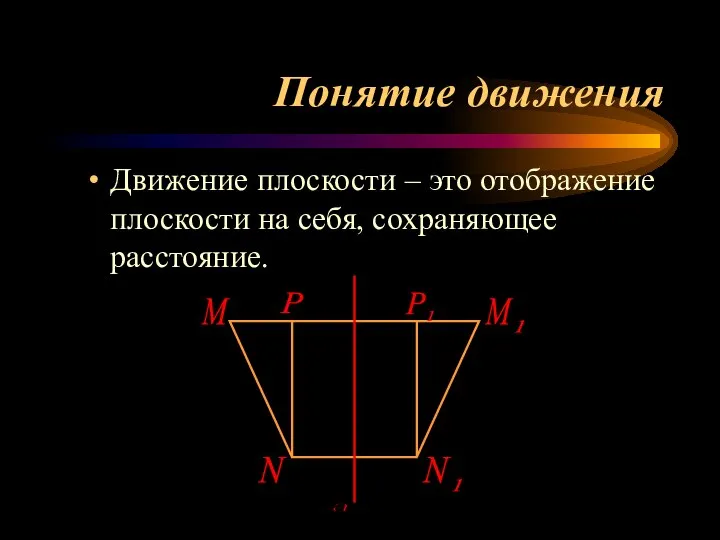
- 5. Понятие движения Движение плоскости – это отображение плоскости на себя, сохраняющее расстояние. М N а Р
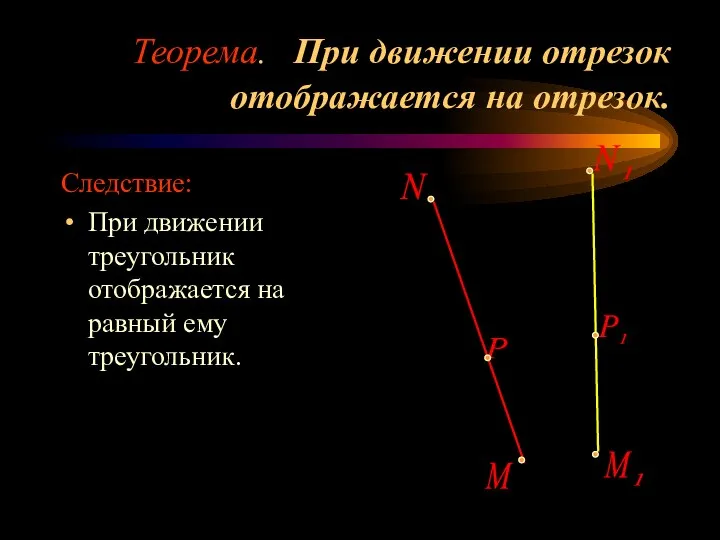
- 6. Теорема. При движении отрезок отображается на отрезок. Следствие: При движении треугольник отображается на равный ему треугольник.
- 7. Наложение Наложение- это отображение плоскости на себя.
- 8. Теорема. Любое движение является наложением. Следствие: При движении любая фигура отображается на равную ей фигуру. Фигуры
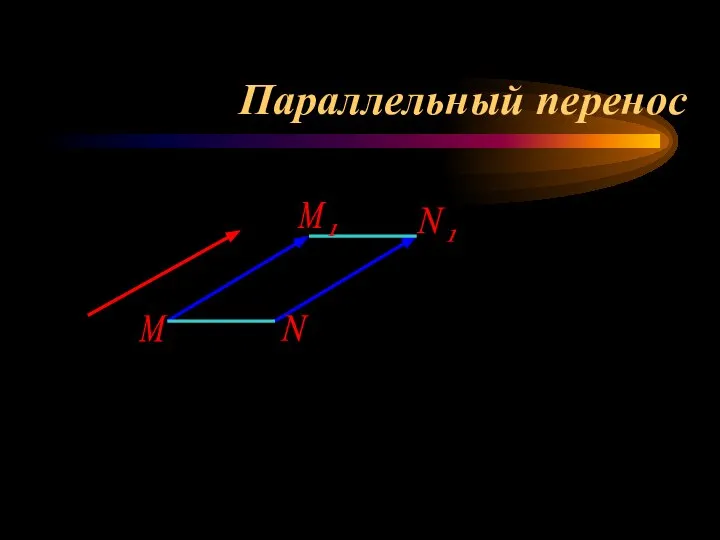
- 9. Параллельный перенос М N
- 10. Параллельный перенос Параллельным переносом называют преобразование плоскости, при котором все точки смещаются по параллельным прямым на
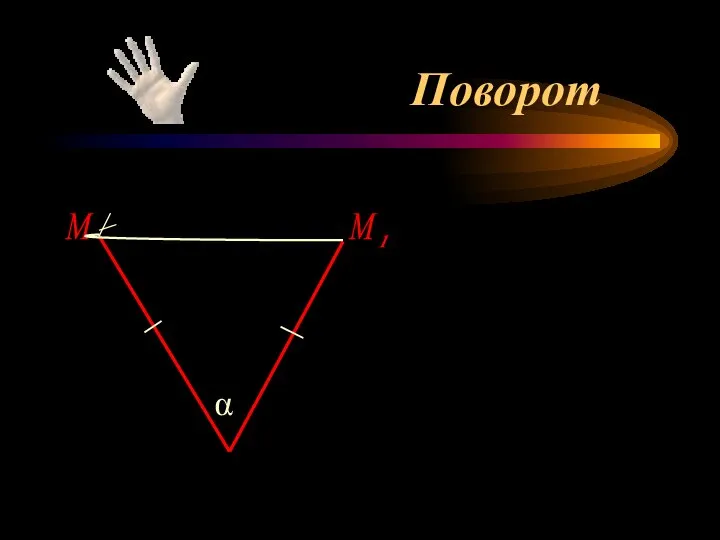
- 11. Поворот М α
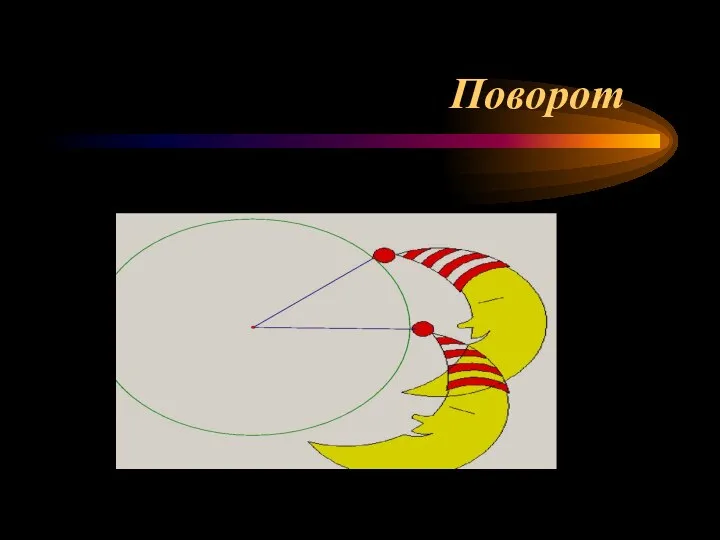
- 12. Поворот
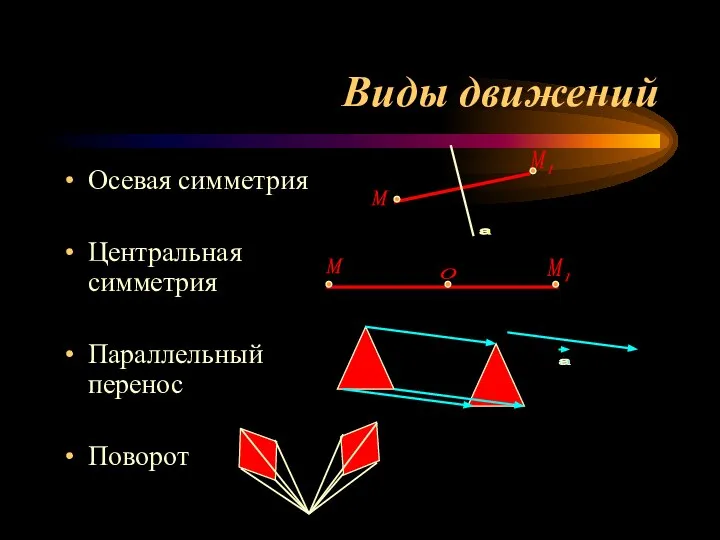
- 13. Виды движений Осевая симметрия Центральная симметрия Параллельный перенос Поворот М М О а а
- 15. Скачать презентацию




 Механическое движение
Механическое движение Материальные расчеты неравновесных ВТП
Материальные расчеты неравновесных ВТП Процесс механической обработки детали кронштейн
Процесс механической обработки детали кронштейн Ножницы как рычаг
Ножницы как рычаг Презентация на тему Геометрическая оптика
Презентация на тему Геометрическая оптика  Тест по теме Электрический ток
Тест по теме Электрический ток Скорость в механическом движении. 7 класс
Скорость в механическом движении. 7 класс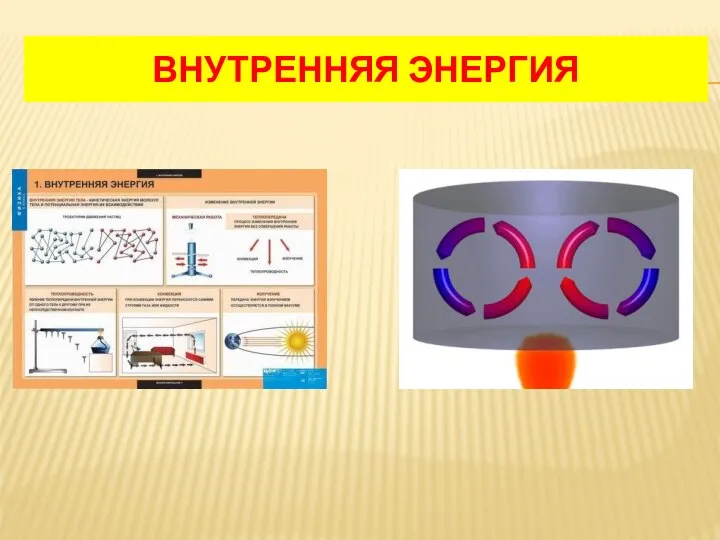 Внутренняя энергия. Агрегатные состояния вещества. Занятие 1. Часть 1
Внутренняя энергия. Агрегатные состояния вещества. Занятие 1. Часть 1 ТMM структура. Лекция 1
ТMM структура. Лекция 1 Автоколебания. Транзистор. Генератор незатухающих колебаний
Автоколебания. Транзистор. Генератор незатухающих колебаний Три состояния вещества
Три состояния вещества Рассеивающие линзы
Рассеивающие линзы Творческое объединение авиаторы
Творческое объединение авиаторы Электрическое сопротивление
Электрическое сопротивление Вода – ее свойства и состояние в природе. 2 класс
Вода – ее свойства и состояние в природе. 2 класс Презентация по физике "Оптические иллюзии или Обман зрения" -
Презентация по физике "Оптические иллюзии или Обман зрения" -  Деформація
Деформація Формула Даламбера. Распространение упругих волн вдоль прямой
Формула Даламбера. Распространение упругих волн вдоль прямой Скорость
Скорость Periodicheskoe
Periodicheskoe Характеристики неявного метода и основные пути решения. Программный комплекс LS-Dyna
Характеристики неявного метода и основные пути решения. Программный комплекс LS-Dyna История и перспективы развития робототехники
История и перспективы развития робототехники Физические явления и интересные факты
Физические явления и интересные факты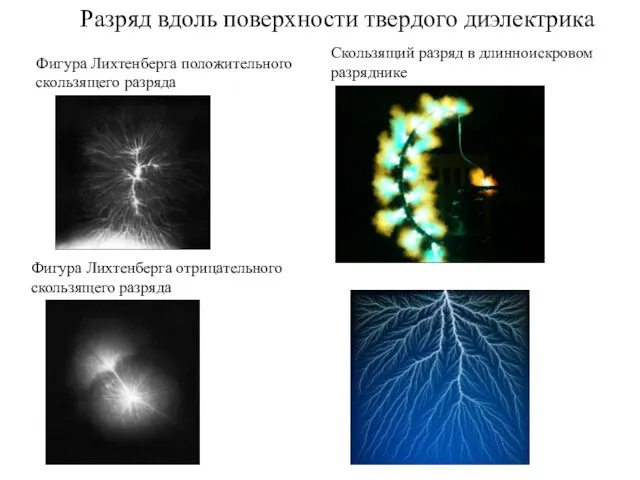 Разряд вдоль поверхности твердого диэлектрика. Лекция 4
Разряд вдоль поверхности твердого диэлектрика. Лекция 4 Бесконтактный метод передачи электрической энергии
Бесконтактный метод передачи электрической энергии Радиоактивные превращения атомных ядер
Радиоактивные превращения атомных ядер Презентация на тему Электризация тел. Два рода зарядов (8 класс)
Презентация на тему Электризация тел. Два рода зарядов (8 класс)  Cокол тысячелетия 10,08
Cокол тысячелетия 10,08