Слайд 2Соотношение I и II законов Ньютона

Слайд 4Динамические уравнения движения
Законы Ньютона ⇨
дифференциальные уравнения (ДУ) = динамические уравнения движения.

Решения динамических уравнений движения ⇨
кинематические уравнения движения,
т.е. зависимости от времени координат и скоростей тел.
Слайд 6Константы интегрирования и начальные условия
Решение с конст-ми интегрирования – общее решение.
Константы интегрирования

⇦ начальные условия (НУ). т.е. значения vx и х в начальный момент времени.
Их подставить в общее решение и найти С:
vx = (Fx /m) t + v0
x = ½(Fx /m) t2 + v0 t + x0
Решение ДУ (и систем ДУ, т.к. нужны еще уравнения для 2 других координат и для других тел) требует некоторых математических навыков.
Поэтому стараются избегать ДУ и получать решения из законов сохранения (ЗС), т.е. соотношений для ФВ, которые сохраняют свои начальные значения при некоторых условиях.
Слайд 8Закон сохранения импульса для замкнутой системы

Слайд 9Закон сохранения и изменения импульса незамкнутой системы

Слайд 11Применимость закона сохранения импульса

Слайд 13Работа и КЭ при криволинейном движении












 Электромагнитные явления
Электромагнитные явления Физика и познание мира
Физика и познание мира Электрический ток в электролитах. Электрическая диссоциация
Электрический ток в электролитах. Электрическая диссоциация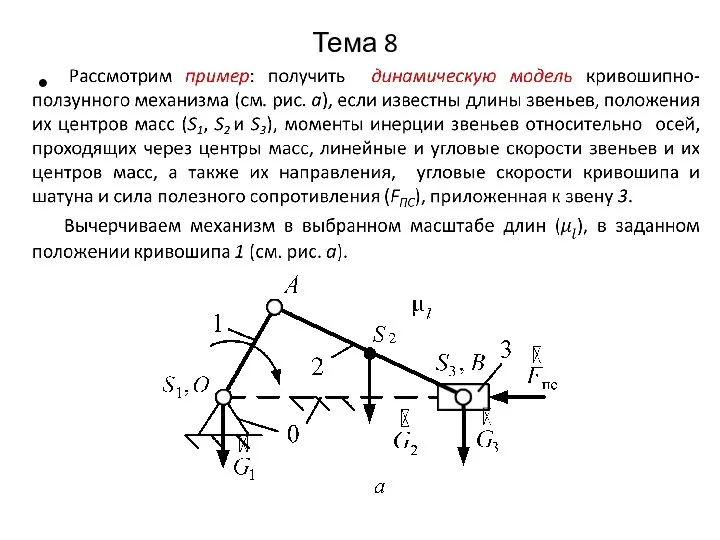 Режимы движения машинных агрегатов и их энергетические характеристики
Режимы движения машинных агрегатов и их энергетические характеристики О науке, Земле и физике
О науке, Земле и физике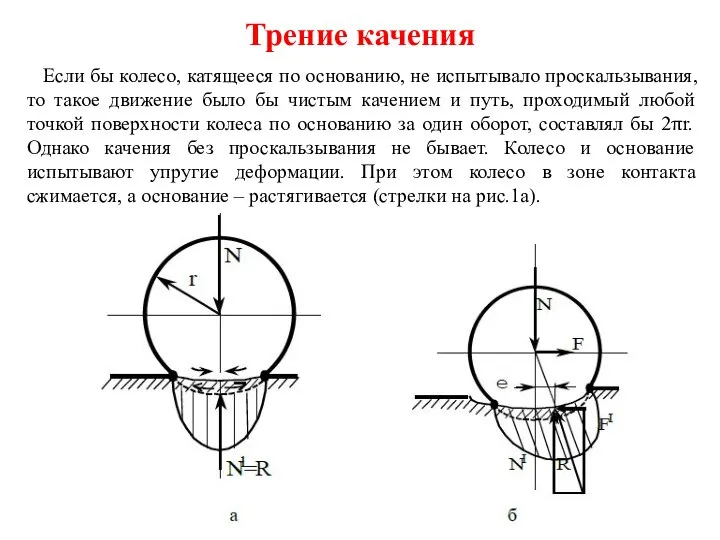 Трение качения
Трение качения Механическое движение
Механическое движение Давление газа
Давление газа Оптика. Закон преломления света
Оптика. Закон преломления света Действия электрического тока
Действия электрического тока Физика и якутский фольклор
Физика и якутский фольклор Почему радуга разноцветная?
Почему радуга разноцветная? трение
трение Закон Архимеда
Закон Архимеда Обозначение трехвинтовых насосов
Обозначение трехвинтовых насосов Сверхпроводимость. Свойства
Сверхпроводимость. Свойства Соединение конденсаторов
Соединение конденсаторов Физическая величина сила
Физическая величина сила Кварки или откуда берется масса
Кварки или откуда берется масса Определите массу воздуха в вашей комнате. Задача
Определите массу воздуха в вашей комнате. Задача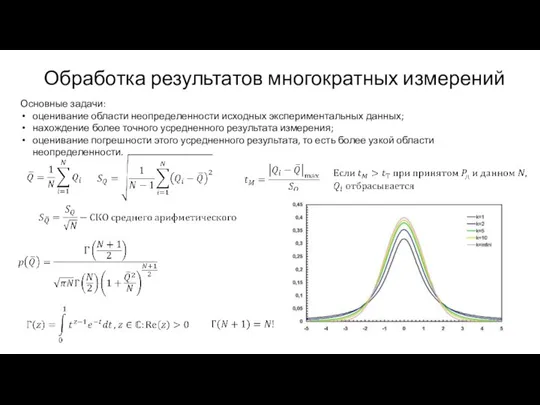 Обработка результатов многократных измерений
Обработка результатов многократных измерений Ядерный реактор. АЭС
Ядерный реактор. АЭС Шарль Огюстен де Кулон
Шарль Огюстен де Кулон Будем знакомы – физика!
Будем знакомы – физика! Степень свободы молекул
Степень свободы молекул Движение тела по окружности под действием силы тяжести
Движение тела по окружности под действием силы тяжести Презентация на тему Гравитационные силы
Презентация на тему Гравитационные силы  Динамометр в домашних условиях и его применение
Динамометр в домашних условиях и его применение