Слайд 2Проблемный вопрос
При произведении расчетов на разностных схемах, важен показатель устойчивости схемы, так-как

при отсутствии устойчивости схемы, расчет не будет сводится к решению разностного уравнения, будет накапливаться большая ошибка в измерениях.
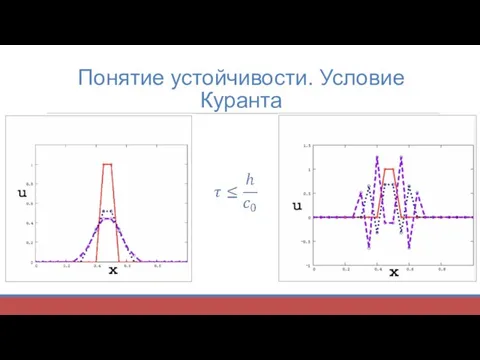
Метод FDTD(Конечных разностей во временной области) основывается на разностной схеме Йе, устойчивость которой обеспечивается за счёт выполнения условия (условия Куранта), для этого необходимо, чтобы множитель в его условии был меньше или равен единице.
В моей работе, передо мной стоит задача доказать путем численных экспериментов, влияние множителя на распространение электромагнитной волны в пространстве.
Слайд 3Понятие устойчивости. Условие Куранта
Слайд 4Метод конечной разности во временной области

Слайд 5Цель
Провести численное исследование устойчивости одномерной схемы Йе
Содержание проекта
Математическая постановка задачи о распространении

электромагнитного импульса в свободном пространстве
Применение метода конечной разности во временной области(FDTD)
Численные эксперименты с разными множителями в условии Куранта
Результаты и их обсуждения
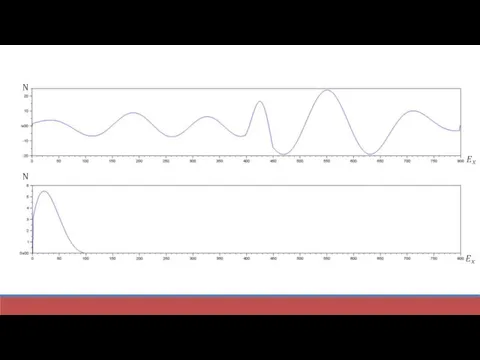
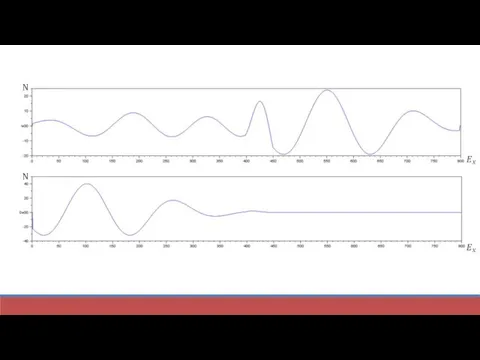
Слайд 9
Вывод
Схема устойчива при множителе равном или меньшем единице. При множителе большем
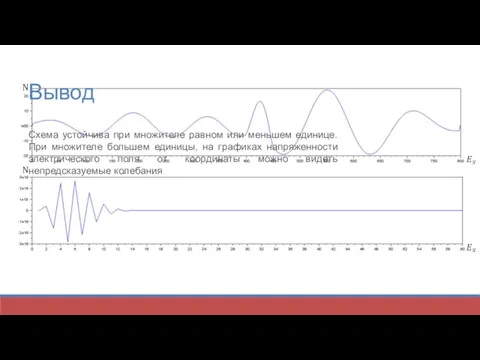
единицы, на графиках напряженности электрического поля от координаты можно видеть непредсказуемые колебания
Слайд 10Итоги работы
Изучилось влияние множителя, входящего в условие Куранта, на устойчивость разностной схемы
Были

изучены свойства разностной схемы
Был реализован метод конечных разностей во временной области
Была изучена научная литература
Были проведены расчеты
Были построены графики
Были численно решены уравнения Максвелла






 Проверочные работы по физике для 7 – 8 класса
Проверочные работы по физике для 7 – 8 класса Геометрическая оптика. Линзы
Геометрическая оптика. Линзы Импульс силы
Импульс силы Закон радиоактивного распада. Решение задач
Закон радиоактивного распада. Решение задач Линзы. Оптическая сила линзы. 9 класс
Линзы. Оптическая сила линзы. 9 класс Физико-механические свойства древесины
Физико-механические свойства древесины Сравнительная характеристика проводниковых материалов. Медь и алюминий
Сравнительная характеристика проводниковых материалов. Медь и алюминий Вода – ее свойства и состояние в природе. 2 класс
Вода – ее свойства и состояние в природе. 2 класс Презентация на тему Магнитный поток
Презентация на тему Магнитный поток  Презентация на тему Применение закона рычага к блоку
Презентация на тему Применение закона рычага к блоку  Лабораторная работа 2. Исследование статических и динамических характеристик источников тока в аналоговых ИС
Лабораторная работа 2. Исследование статических и динамических характеристик источников тока в аналоговых ИС Влияние электромагнитных волн на организм человека
Влияние электромагнитных волн на организм человека Основы взаимозаменяемости и технические измерения
Основы взаимозаменяемости и технические измерения Опыты с водой (для дошкольников)
Опыты с водой (для дошкольников) Законы физики в танцевальных движениях
Законы физики в танцевальных движениях Коливальний рух. Амплітуда коливань. Період коливань. Маятники
Коливальний рух. Амплітуда коливань. Період коливань. Маятники Закон Ома и удельное сопротивление проводника. Решение задач
Закон Ома и удельное сопротивление проводника. Решение задач Квантовая физика твердого тела
Квантовая физика твердого тела Квантовая биофизика
Квантовая биофизика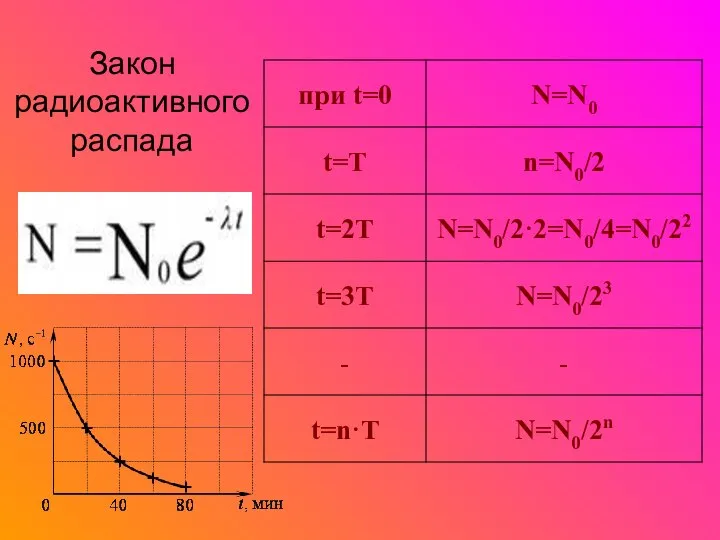 Закон радиоактивного распада
Закон радиоактивного распада Влияние электромагнитного поля на размер феромагнетика в трасформаторе
Влияние электромагнитного поля на размер феромагнетика в трасформаторе Физика в нашей жизни
Физика в нашей жизни Презентация на тему Исследование силы трения скольжения
Презентация на тему Исследование силы трения скольжения  Презентация по физике "Его Величество - Электричество" -
Презентация по физике "Его Величество - Электричество" -  2. Механические, конструкционные и эксплуатационные свойства материалов
2. Механические, конструкционные и эксплуатационные свойства материалов Радиационная гигиена
Радиационная гигиена Значение режима смазывания для увеличения долговечности работы машин и механизмов
Значение режима смазывания для увеличения долговечности работы машин и механизмов Газовые законы
Газовые законы