Содержание
- 2. Нет ничего более упорядоченного, чем природа. Мировой организм есть неразрывное целое. Все элементы мироздания гармонично связаны
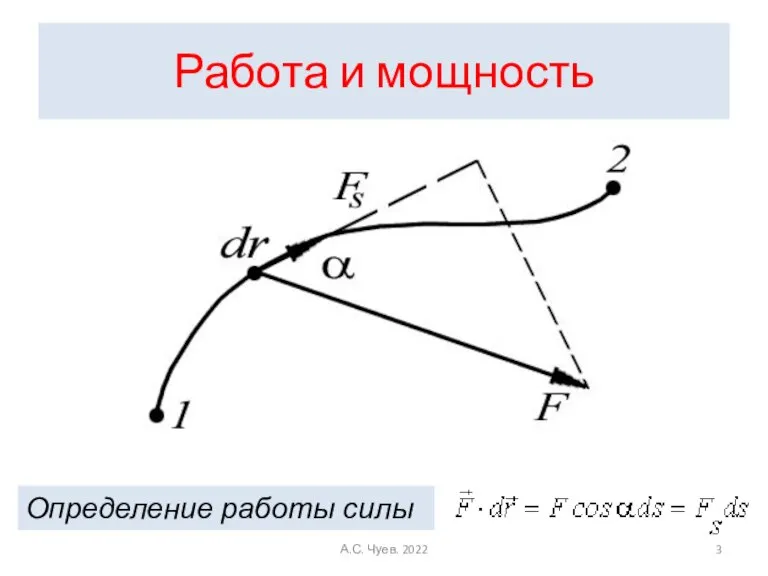
- 3. Работа и мощность Определение работы силы А.С. Чуев. 2022
- 4. А.С. Чуев. 2022
- 5. Элементарная работа силы Интегральная работа силы А.С. Чуев. 2022
- 6. Мощность - это работа, совершаемая силой (в механике) за единицу времени Для работы: Для мощности: А.С.
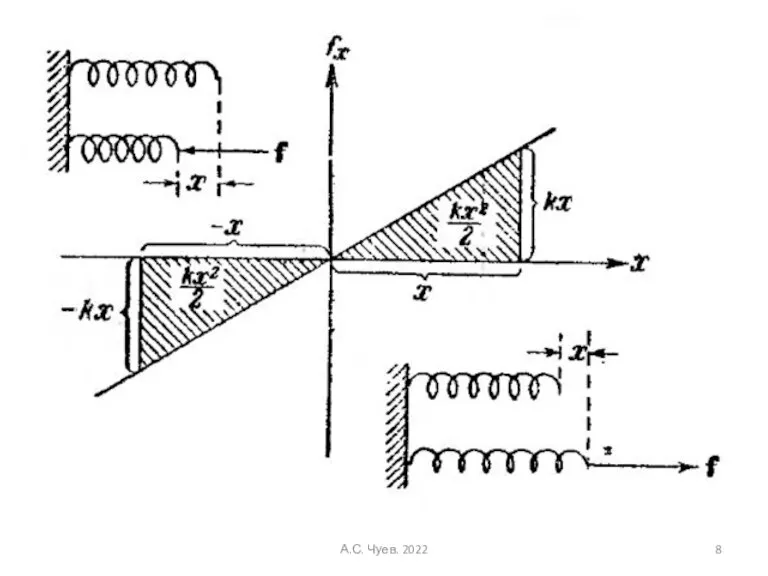
- 7. Потенциальная энергия и работа упругой деформации (пружины) Закон Гука. Сила упругости Сила непостоянна, поэтому элементарная работа
- 8. А.С. Чуев. 2022
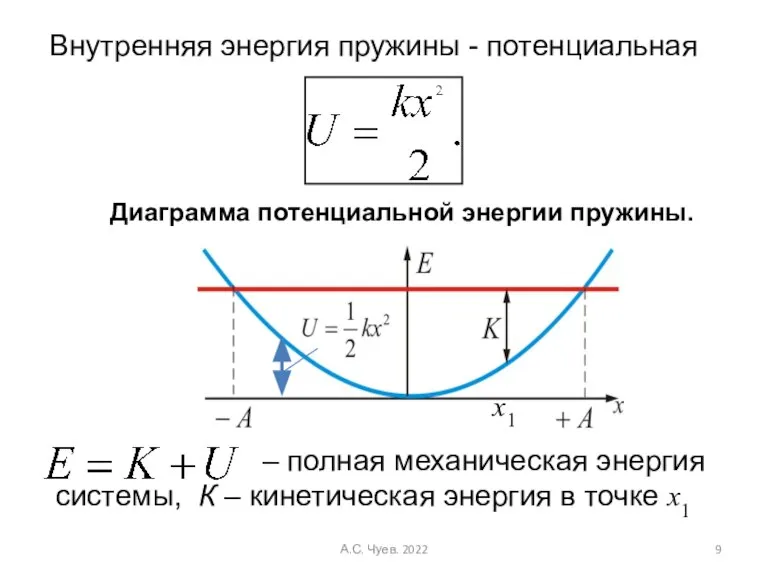
- 9. Диаграмма потенциальной энергии пружины. – полная механическая энергия системы, К – кинетическая энергия в точке x1
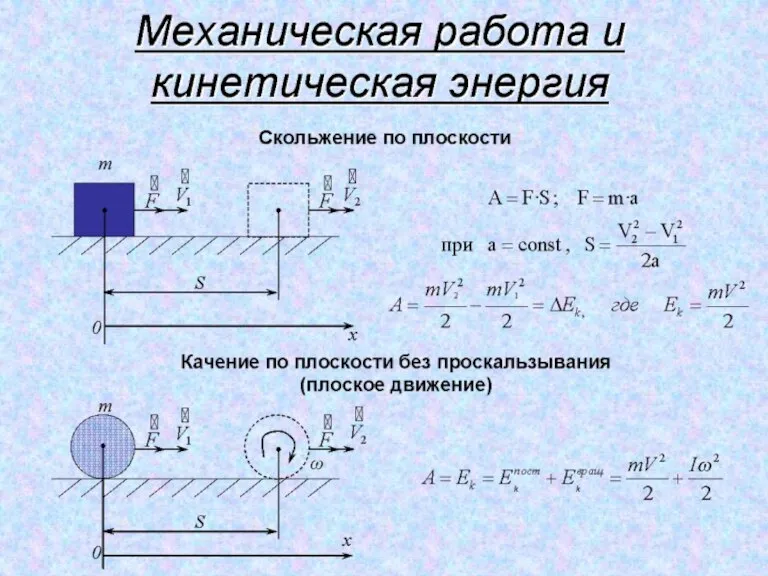
- 10. Кинетической энергией поступательного движения называется соотношение: K – аддитивная величина: К - является функцией состояния системы
- 11. отсюда Связь кинетической энергии с импульсом Т.к. Связь кинетической энергии с работой работа силы приложенной к
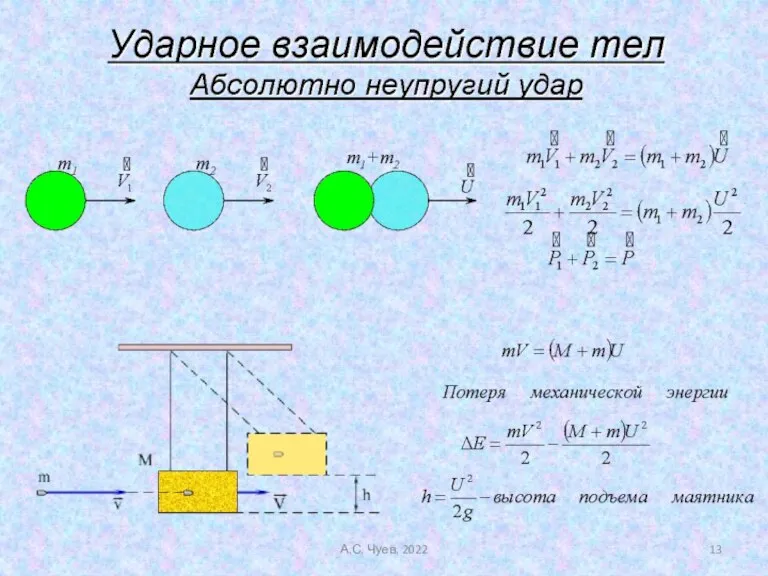
- 13. А.С. Чуев. 2022
- 14. Работа, энергия и мощность при вращательном движении А.С. Чуев. 2022
- 15. Сила называется консервативной или потенциальной, если её работа не зависит от траектории, а определяется только начальным
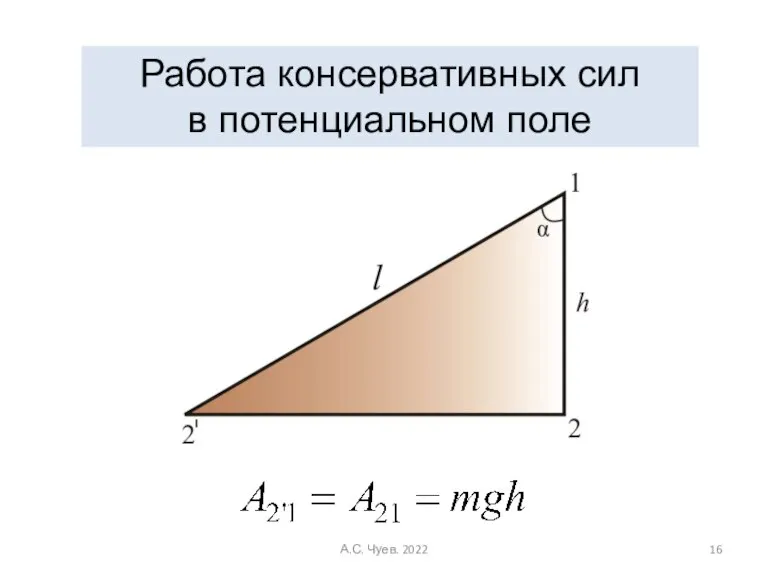
- 16. Работа консервативных сил в потенциальном поле А.С. Чуев. 2022
- 17. Потенциальная энергия Если в системе материальных тел действуют консервативные силы, то можно ввести понятие потенциальной энергии.
- 18. (*) здесь потенциальная энергия U (х, у, z) – функция состояния системы, зависящая только от координат
- 19. Работа силы тяжести А.С. Чуев. 2022
- 20. Нет единого выражения для U. В разных случаях она определяется по-разному. Потенциальная энергия при гравитационном взаимодействии
- 21. Для случая гравитационного взаимодействия между массами M и m, находящимися на расстоянии r друг от друга,
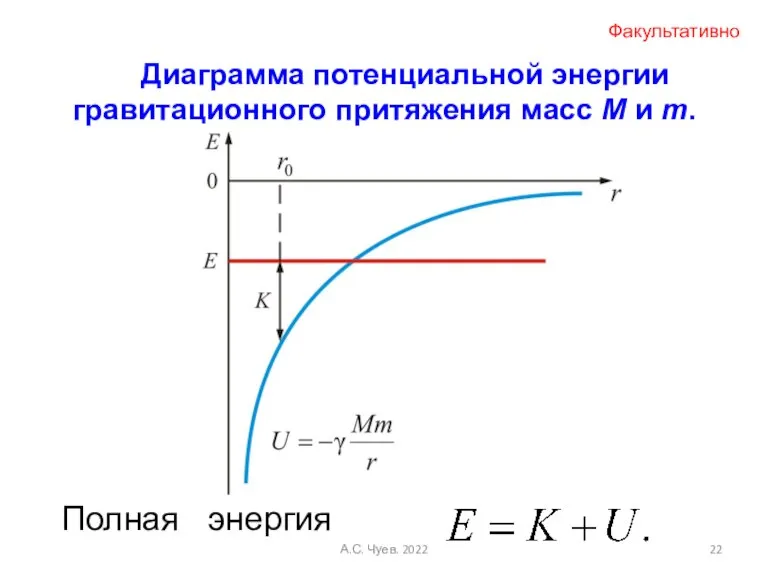
- 22. Полная энергия Диаграмма потенциальной энергии гравитационного притяжения масс M и m. Факультативно А.С. Чуев. 2022
- 23. Этим слагаемым можно пренебречь Факультативно А.С. Чуев. 2022
- 24. Динамика орбитального движения планет - кинетическая энергия - потенциальная энергия Факультативно А.С. Чуев. 2022
- 25. Факультативно А.С. Чуев. 2022
- 26. Факультативно А.С. Чуев. 2022
- 27. Факультативно А.С. Чуев. 2022
- 28. А.С. Чуев. 2022 Факультативно
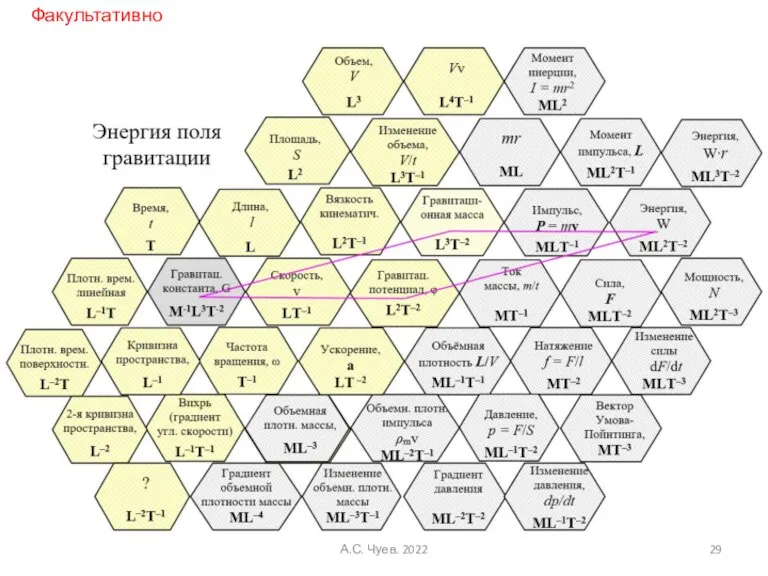
- 29. А.С. Чуев. 2022 Факультативно
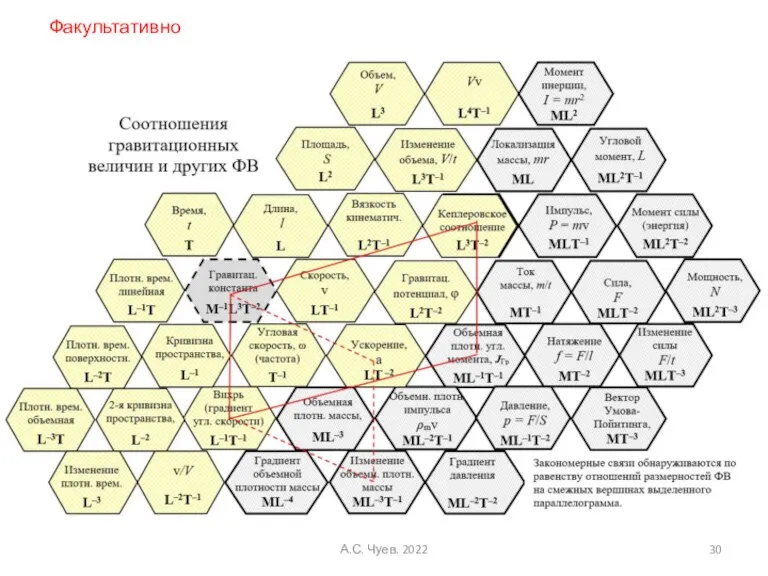
- 30. А.С. Чуев. 2022 Факультативно
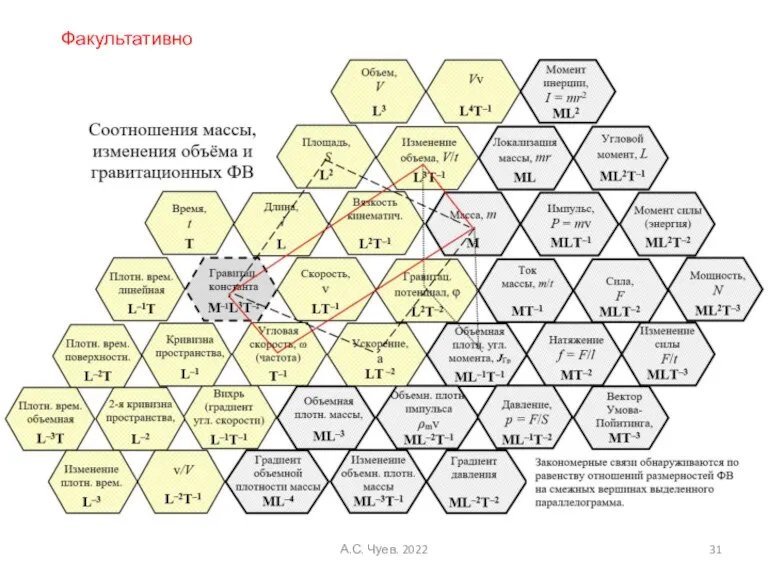
- 31. А.С. Чуев. 2022 Факультативно
- 32. ТЕОРЕМА О ВИРИАЛЕ Средняя кинетическая энергия материальной точки, совершающей пространственно ограниченное движение под действием сил притяжения,
- 33. Связь между потенциальной энергией и силой Пространство, в котором действуют консервативные силы, называется потенциальным полем. Каждой
- 34. Проекции вектора силы на оси координат: А.С. Чуев. 2022
- 35. Через проекции вектор силы записывается так: или более коротко где А.С. Чуев. 2022
- 36. Градиент – это вектор, показывающий направление наибыстрейшего увеличения функции. В формуле стоит знак «минус», что означает
- 37. Закон сохранения механической энергии В сороковых годах девятнадцатого века трудами Р. Майера, Г. Гельмгольца и Дж.
- 38. Для консервативной системы частиц полная энергия системы: Для механической энергии закон сохранения звучит так: полная механическая
- 39. Для замкнутой системы, т.е. для системы на которую не действуют внешние силы, можно записать: т.е. полная
- 40. Если в замкнутой системе действуют неконсервативные силы, то полная механическая энергия системы не сохраняется – частично
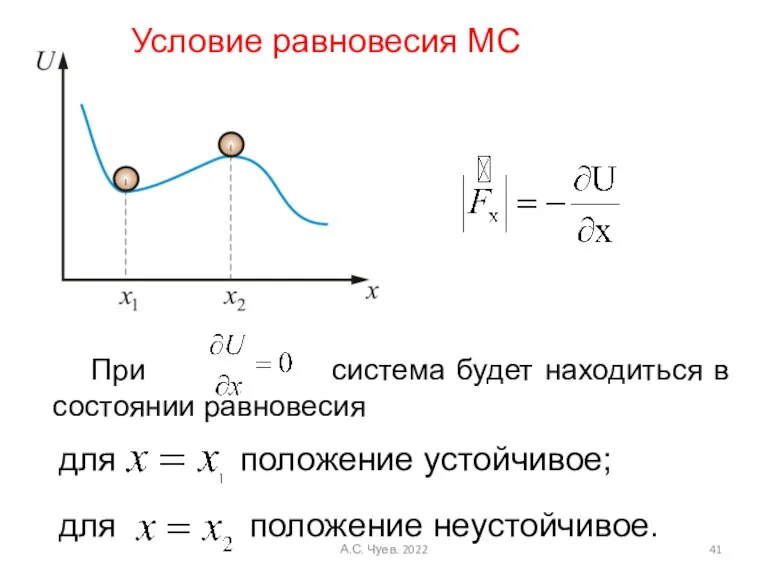
- 41. При система будет находиться в состоянии равновесия для положение устойчивое; для положение неустойчивое. Условие равновесия МС
- 42. Превращения энергии А.С. Чуев. 2022
- 43. А.С. Чуев. 2022
- 44. А.С. Чуев. 2022
- 45. А.С. Чуев. 2022
- 46. Законы сохранения и причина их действия по теореме Э. Нётер А.С. Чуев. 2022
- 47. Факультативно А.С. Чуев. 2022
- 48. Факультативно А.С. Чуев. 2022
- 50. Скачать презентацию
































 Построение кривых потребных тяг Жуковского
Построение кривых потребных тяг Жуковского Конструирование и прототипирование прокатной клети ДУО 65
Конструирование и прототипирование прокатной клети ДУО 65 Последовательное соединение
Последовательное соединение Изучение структуры закрученного потока не сжимаемой жидкости
Изучение структуры закрученного потока не сжимаемой жидкости Почему радуга разноцветная?
Почему радуга разноцветная? Презентация на тему Атмосферное давление: тест
Презентация на тему Атмосферное давление: тест  Методы, основанные на индуцированном переходе из одной фазы в другую через разделяющую их третью фазу. (Лекция 7)
Методы, основанные на индуцированном переходе из одной фазы в другую через разделяющую их третью фазу. (Лекция 7) Оптические явления во сне и наяву
Оптические явления во сне и наяву Май күпдеші озған өткізгіш материал және оның парамтрі
Май күпдеші озған өткізгіш материал және оның парамтрі Электромагнетизм
Электромагнетизм Корабли современные
Корабли современные Презентация на тему Равновесие тел
Презентация на тему Равновесие тел  Применение первого начала термодинамики к изопроцессам
Применение первого начала термодинамики к изопроцессам Постоянные магниты
Постоянные магниты Влияние облучения мягким рентгеновским излучением на элементный приповерхностный состав полупроводника CdHgTe
Влияние облучения мягким рентгеновским излучением на элементный приповерхностный состав полупроводника CdHgTe Виды тепловых двигателей
Виды тепловых двигателей Потенциальная энергия. (Лекция 4)
Потенциальная энергия. (Лекция 4) Определение электромагнитного поля. Практическое занятие
Определение электромагнитного поля. Практическое занятие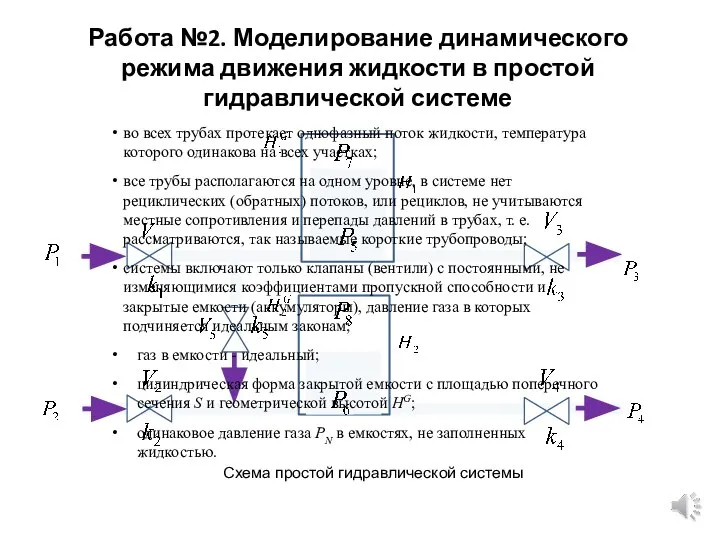 Моделирование динамического режима движения жидкости в простой гидравлической системе. Работа №2
Моделирование динамического режима движения жидкости в простой гидравлической системе. Работа №2 Презентация на тему Энергетические характеристики электрического поля
Презентация на тему Энергетические характеристики электрического поля  Инструкция по наладке узла управления отопления по независимой схеме
Инструкция по наладке узла управления отопления по независимой схеме Презентация по физике "Энергия ядра. Взгляд в будущее" -
Презентация по физике "Энергия ядра. Взгляд в будущее" -  Презентация на тему Инфракрасное и ультрафиолетовое излучения
Презентация на тему Инфракрасное и ультрафиолетовое излучения  Задачи по физике. Вариант №1
Задачи по физике. Вариант №1 Презентация на тему Единицы массы
Презентация на тему Единицы массы  Проект Jaguar
Проект Jaguar Как устроен атом
Как устроен атом Теория линейных электрических цепей
Теория линейных электрических цепей