Электрическое поле

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ХАРАКТЕРИЗУЕТСЯ ВОЗДЕЙСТВИЕМ НА ЭЛЕКТРО ЗАРЯЖЕННУЮ ЧАСТИЦУ С СИЛОЙ ПРОПОРЦИОНАЛЬНОЙ ЗАРЯДА ЧАСТИЦЫ И НЕЗАВИСЯЩЕЙ ОТ ЕЕ СКОРОСТИ.
ДЛЯ КОЛИЧЕСТВЕННОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ВВОДИТСЯ СИЛОВАЯ ХАРАКТЕРИСТИКА — НАПРЯЖЁННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.

НАПРЯЖЁННОСТЬ — ВЕКТОРНАЯ ВЕЛИЧИНА ОПРЕДЕЛЯЮЩАЯ СИЛУ ДЕЙСТВУЮЩУЮ НА ЗАРЯЖЕННУЮ ЧАСТИЦУ ИЛИ ТЕЛО СО СТОРОНЫ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И ЧИСЛЕННО РАВНАЯ ОТНОШЕНИЮ СИЛЫ К ЗАРЯДУ ЧАСТИЦЫ.
НАПРЯЖЁННОСТЬ — ЭТО ОСНОВНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОТОРАЯ ИЗМЕРЯЕТ ИНТЕНСИВНОСТЬ ПОЛЯ.

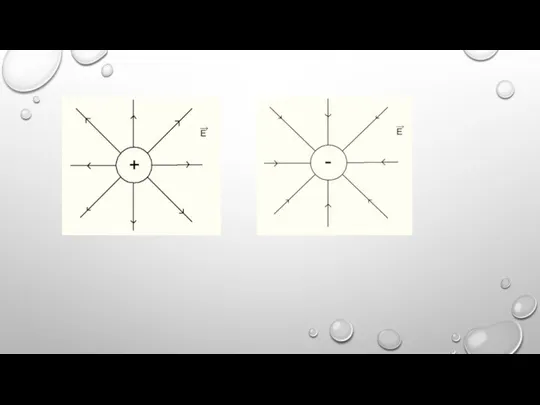
НАПРАВЛЕНИЕ ВЕКТОРА НАПРЯЖЁННОСТИ СОВПАДАЕТ С НАПРАВЛЕНИЕМ СИЛЫ ДЕЙСТВУЮЩЕЙ НА ЧАСТИЦУ С ПОЛОЖИТЕЛЬНЫМ ЗАРЯДОМ.
Е = F/Q, [Н/КЛ ИЛИ B/M]
ГДЕ
- F – СИЛА;
- Q - ЗАРЯД ЧАСТИЦЫ.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ НАЗЫВАЕТСЯ ОДНОРОДНЫМ (РАВНОМЕРНЫМ) ЕСЛИ НАПРЯЖЁННОСТЬ ПОЛЯ ВО ВСЕХ ТОЧКАХ ОДИНАКОВОЕ ПО ВЕЛИЧИНЕ И НАПРАВЛЕНИЮ.
ЭЛЕКТРИ́ЧЕСКОЕ НАПРЯЖЕ́НИЕ МЕЖДУ ТОЧКАМИ A И B ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ИЛИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ — ФИЗИЧЕСКАЯ ВЕЛИЧИНА, ЗНАЧЕНИЕ КОТОРОЙ РАВНО РАБОТЕ ЭФФЕКТИВНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ (ВКЛЮЧАЮЩЕГО СТОРОННИЕ ПОЛЯ), СОВЕРШАЕМОЙ ПРИ ПЕРЕНОСЕ ЕДИНИЧНОГО ПРОБНОГО ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ИЗ ТОЧКИ A В ТОЧКУ B.

ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНИЕ (U) — ЭТО РАБОТА (А) СОВЕРШАЕМАЯ СИЛОЙ ПОЛЯ ПО ПЕРЕМЕЩЕНИЮ ЗАРЯЖЕННЫХ ЧАСТИЦ МЕЖДУ ДВУМЯ ТОЧКАМИ ПОЛЯ.
U = A/Q, [B]
ГДЕ
- А – РАБОТА;
- Q – ЭЛЕКТРИЧЕСКИЙ ЗАРЯД.

ПОТЕНЦИАЛ - ЭНЕРГЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ПОЛЯ В ДАННОЙ ТОЧКЕ. ПОТЕНЦИАЛ НЕ ЗАВИСИТ ОТ ВЕЛИЧИНЫ ЗАРЯДА, ПОМЕЩЕННОГО В ЭТО ПОЛЕ.
ПОТЕНЦИАЛ (Φ) — ЭТО ЭНЕРГЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ПОЛЯ ЧИСЛЕННО РАВНАЯ ОТНОШЕНИЮ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ ЗАРЯЖЕННОЙ ЧАСТИЦЫ ПОМЕЩЕННОЙ В ДАННОЙ ТОЧКЕ ПОЛЯ ВЕЛИЧИНЕ ЕЁ ЗАРЯДА.

Φ = W/Q, [В]
ГДЕ
- W – ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОЙ ЧАСТИЦЫ;
- Q – ВЕЛИЧИНА ЗАРЯДА.

РАЗНОСТЬ ПОТЕНЦИАЛОВ (НАПРЯЖЕНИЕ) МЕЖДУ 2-МЯ ТОЧКАМИ ПОЛЯ РАВНЯЕТСЯ ОТНОШЕНИЮ РАБОТЫ ПОЛЯ ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА ИЗ НАЧАЛЬНОЙ ТОЧКИ В КОНЕЧНУЮ К ЭТОМУ ЗАРЯДУ. ТАК КАК РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА В ПОТЕНЦИАЛЬНОМ ПОЛЕ НЕ ЗАВИСИТ ОТ ФОРМЫ ТРАЕКТОРИИ , ТО, ЗНАЯ НАПРЯЖЕНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ, МЫ ОПРЕДЕЛИМ РАБОТУ, КОТОРАЯ СОВЕРШАЕТСЯ ПОЛЕМ ПО ПЕРЕМЕЩЕНИЮ ЕДИНИЧНОГО ЗАРЯДА.

РАЗНОСТЬ ПОТЕНЦИАЛОВ (НАПРЯЖЕНИЕ) МЕЖДУ 2-МЯ ТОЧКАМИ ПОЛЯ РАВНЯЕТСЯ ОТНОШЕНИЮ РАБОТЫ ПОЛЯ ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА ИЗ НАЧАЛЬНОЙ ТОЧКИ В КОНЕЧНУЮ К ЭТОМУ ЗАРЯДУ:

ТАК КАК РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА В ПОТЕНЦИАЛЬНОМ ПОЛЕ НЕ ЗАВИСИТ ОТ ФОРМЫ ТРАЕКТОРИИ, ТО, ЗНАЯ НАПРЯЖЕНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ, МЫ ОПРЕДЕЛИМ РАБОТУ, КОТОРАЯ СОВЕРШАЕТСЯ ПОЛЕМ ПО ПЕРЕМЕЩЕНИЮ ЕДИНИЧНОГО ЗАРЯДА.

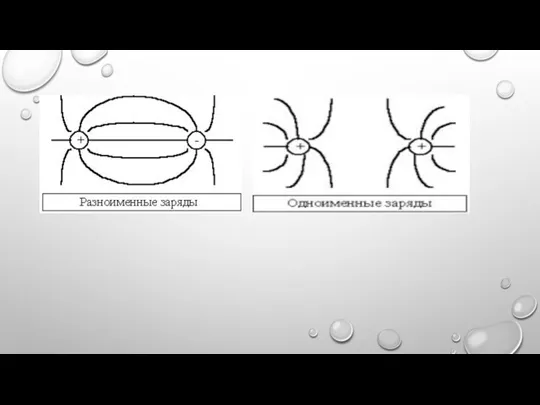
ЕСЛИ ЕСТЬ НЕСКОЛЬКО ТОЧЕЧНЫХ ЗАРЯДОВ, ЗНАЧИТ, ПОТЕНЦИАЛ ПОЛЯ В НЕКОТОРОЙ ТОЧКЕ ПРОСТРАНС­ТВА ОПРЕДЕЛЯЕТСЯ КАК АЛГЕБРАИЧЕСКАЯ СУММА ПОТЕНЦИАЛОВ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ КАЖДОГО ЗАРЯДА В ДАННОЙ ТОЧКЕ:

ВЛИЯНИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
ПРОВОДНИКИ
ПРОВОДНИКАМИ НАЗЫВАЮТСЯ ТЕЛА, СПОСОБНЫЕ ПРОПУСКАТЬ ЧЕРЕЗ СЕБЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКАМИ ЯВЛЯЮТСЯ МЕТАЛЛЫ, ЖИДКИЕ РАСТВОРЫ И РАСПЛАВЫ ЭЛЕКТРОЛИТОВ. СВОБОДНЫМИ ЗАРЯДАМИ В МЕТАЛЛЕ ЯВЛЯЮТСЯ ЭЛЕКТРОНЫ ВНЕШНИХ ОБОЛОЧЕК АТОМОВ, ПОТЕРЯВШИЕ С НИМИ СВЯЗЬ. ЭТИ ЭЛЕКТРОНЫ, НАЗЫВАЕМЫЕ СВОБОДНЫМИ ЭЛЕКТРОНАМИ, МОГУТ СВОБОДНО ДВИГАТЬСЯ ПО МЕТАЛЛИЧЕСКОМУ ТЕЛУ В ЛЮБОМ НАПРАВЛЕНИИ. В РАСТВОРАХ СОЛЕЙ СВОБОДНЫМИ ЗАРЯДАМИ СЛУЖАТ ПОЛОЖИТЕЛЬНО И ОТРИЦАТЕЛЬНО ЗАРЯЖЕННЫЕ ИОНЫ.

ДИЭЛЕКТРИКИ
В ОТЛИЧИЕ ОТ ПРОВОДНИКОВ, В ИДЕАЛЬНЫХ ДИЭЛЕКТРИКАХ (ИЗОЛЯТОРАХ) НЕТ СВОБОДНЫХ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ. ОНИ СОСТОЯТ ИЗ НЕЙТРАЛЬНЫХ АТОМОВ ИЛИ МОЛЕКУЛ. ЗАРЯЖЕННЫЕ ЧАСТИЦЫ В НЕЙТРАЛЬНОМ АТОМЕ СВЯЗАНЫ ДРУГ С ДРУГОМ И НЕ МОГУТ ПЕРЕМЕЩАТЬСЯ ПОД ДЕЙСТВИЕМ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ПО ВСЕМУ ОБЪЕМУ ДИЭЛЕКТРИКА.

ПРИ ВНЕСЕНИИ ДИЭЛЕКТРИКА ВО ВНЕШНЕЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ E˳ В НЕМ ВОЗНИКАЕТ НЕКОТОРОЕ ПЕРЕРАСПРЕДЕЛЕНИЕ ЗАРЯДОВ, ВХОДЯЩИХ В СОСТАВ АТОМОВ ИЛИ МОЛЕКУЛ. В РЕЗУЛЬТАТЕ ТАКОГО ПЕРЕРАСПРЕДЕЛЕНИЯ НА ПОВЕРХНОСТИ ДИЭЛЕКТРИЧЕСКОГО ОБРАЗЦА ПОЯВЛЯЮТСЯ ИЗБЫТОЧНЫЕ НЕСКОМПЕНСИРОВАННЫЕ СВЯЗАННЫЕ ЗАРЯДЫ. ВСЕ ЗАРЯЖЕННЫЕ ЧАСТИЦЫ, ОБРАЗУЮЩИЕ МАКРОСКОПИЧЕСКИЕ СВЯЗАННЫЕ ЗАРЯДЫ, ПО-ПРЕЖНЕМУ ВХОДЯТ В СОСТАВ СВОИХ АТОМОВ.

КОНДЕНСА́ТОР (ОТ ЛАТ. CONDENSARE — «УПЛОТНЯТЬ», «СГУЩАТЬ» ИЛИ ОТ ЛАТ. CONDENSATIO — «НАКОПЛЕНИЕ») — ДВУХПОЛЮСНИК С ОПРЕДЕЛЁННЫМ ИЛИ ПЕРЕМЕННЫМ ЗНАЧЕНИЕМ ЁМКОСТИ[1] И МАЛОЙ ПРОВОДИМОСТЬЮ; УСТРОЙСТВО ДЛЯ НАКОПЛЕНИЯ ЗАРЯДА И ЭНЕРГИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.

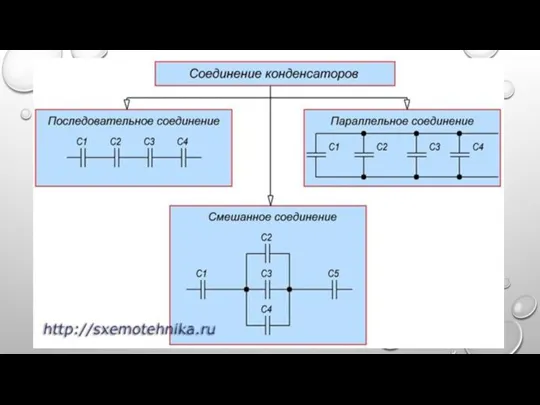
СОЕДИНЕНИЕ КОНДЕНСАТОРОВ
В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ПРИМЕНЯЮТСЯ РАЗЛИЧНЫЕ СПОСОБЫ СОЕДИНЕНИЯ КОНДЕНСАТОРОВ. СОЕДИНЕНИЕ КОНДЕНСАТОРОВ МОЖЕТ ПРОИЗВОДИТЬСЯ: ПОСЛЕДОВАТЕЛЬНО, ПАРАЛЛЕЛЬНО И ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНО (ПОСЛЕДНЕЕ ИНОГДА НАЗЫВАЮТ СМЕШАННОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ). СУЩЕСТВУЮЩИЕ ВИДЫ СОЕДИНЕНИЯ КОНДЕНСАТОРОВ ПОКАЗАНЫ НА РИСУНКЕ 1.

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ.
ЕСЛИ ГРУППА КОНДЕНСАТОРОВ ВКЛЮЧЕНА В ЦЕПЬ ТАКИМ ОБРА­ЗОМ, ЧТО К ТОЧКАМ ВКЛЮЧЕНИЯ НЕПОСРЕДСТВЕННО ПРИСОЕДИНЕНЫ ПЛАСТИНЫ ВСЕХ КОНДЕНСАТОРОВ, ТО ТАКОЕ СОЕДИНЕНИЕ НАЗЫВАЕТСЯ ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ КОНДЕНСАТОРОВ (РИСУНОК 2.).

ПРИ ЗАРЯДЕ ГРУППЫ КОНДЕНСАТОРОВ, СОЕДИНЕННЫХ ПАРАЛЛЕЛЬ­НО, МЕЖДУ ПЛАСТИНАМИ ВСЕХ КОНДЕНСАТОРОВ БУДЕТ ОДНА И ТА ЖЕ РАЗНОСТЬ ПОТЕНЦИАЛОВ, ТАК КАК ВСЕ ОНИ ЗАРЯЖАЮТСЯ ОТ ОДНОГО И ТОГО ЖЕ ИСТОЧНИКА ТОКА. ОБЩЕЕ ЖЕ КОЛИЧЕ­СТВО ЭЛЕКТРИЧЕСТВА НА ВСЕХ КОНДЕНСАТОРАХ БУДЕТ РАВНО СУММЕ КОЛИЧЕСТВ ЭЛЕКТРИЧЕСТВА, ПОМЕЩАЮЩИХСЯ НА КАЖДОМ ИЗ КОН­ДЕНСАТОРОВ, ТАК КАК ЗАРЯД КАЖДОГО ИХ КОНДЕНСАТОРОВ ПРОИС­ХОДИТ НЕЗАВИСИМО ОТ ЗАРЯДА ДРУГИХ КОНДЕНСАТОРОВ ДАННОЙ ГРУППЫ. ИСХОДЯ ИЗ ЭТОГО, ВСЮ СИСТЕМУ ПАРАЛЛЕЛЬНО СОЕДИНЕН­НЫХ КОНДЕНСАТОРОВ МОЖНО РАССМАТРИВАТЬ КАК ОДИН ЭКВИВА­ЛЕНТНЫЙ (РАВНОЦЕННЫЙ) КОНДЕНСАТОР. ТОГДА ОБЩАЯ ЕМКОСТЬ КОНДЕНСАТОРОВ ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ РАВНА СУММЕ ЕМКОСТЕЙ ВСЕХ СОЕДИНЕННЫХ КОНДЕНСАТОРОВ.

ОБОЗНАЧИМ СУММАРНУЮ ЕМКОСТЬ СОЕДИНЕННЫХ В БАТАРЕЮ КОНДЕНСАТОРОВ БУК­ВОЙ СОБЩ, ЕМКОСТЬ ПЕРВОГО КОНДЕНСАТОРА С1 ЕМКОСТЬ ВТОРОГО С2 И ЕМКОСТЬ ТРЕТЬЕГО С3. ТОГДА ДЛЯ ПАРАЛЛЕЛЬНОГО СОЕДИНЕНИЯ КОНДЕНСАТОРОВ БУДЕТ СПРАВЕДЛИВА СЛЕДУЮЩАЯ ФОРМУЛА:

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ.
ЕСЛИ ЖЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ В БАТАРЕЮ ПРОИЗВОДИТСЯ В ВИДЕ ЦЕПОЧКИ И К ТОЧКАМ ВКЛЮЧЕНИЯ В ЦЕПЬ НЕПОСРЕДСТВЕННО ПРИСОЕДИНЕНЫ ПЛАСТИНЫ ТОЛЬКО ПЕРВОГО И ПОСЛЕДНЕГО КОНДЕНСАТОРОВ, ТО ТАКОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ НАЗЫВАЕТСЯ ПОСЛЕДО­ВАТЕЛЬНЫМ (РИСУНОК 3).

ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ ВСЕ КОНДЕНСА­ТОРЫ ЗАРЯЖАЮТСЯ ОДИНАКОВЫМ КОЛИЧЕСТВОМ ЭЛЕКТРИЧЕСТВА, ТАК КАК НЕПОСРЕДСТВЕННО ОТ ИСТОЧНИКА ТОКА ЗАРЯЖАЮТСЯ ТОЛЬКО КРАЙНИЕ ПЛАСТИНЫ (1 И 6), А ОСТАЛЬНЫЕ ПЛАСТИНЫ (2, 3, 4 И 5) ЗАРЯ­ЖАЮТСЯ ЧЕРЕЗ ВЛИЯНИЕ. ПРИ ЭТОМ ЗАРЯД ПЛА­СТИНЫ 2 БУДЕТ РАВЕН ПО ВЕЛИЧИНЕ И ПРОТИВО­ПОЛОЖЕН ПО ЗНАКУ ЗА­РЯДУ ПЛАСТИНЫ 1, ЗАРЯД ПЛАСТИНЫ 3 БУДЕТ РАВЕН ПО ВЕЛИЧИНЕ И ПРОТИВОПОЛОЖЕН ПО ЗНАКУ ЗАРЯДУ ПЛА­СТИНЫ 2 И Т. Д.
НАПРЯЖЕНИЯ НА РАЗЛИЧНЫХ КОНДЕНСАТОРАХ БУДУТ, ВООБЩЕ ГОВОРЯ, РАЗЛИЧНЫМИ, ТАК КАК ДЛЯ ЗАРЯДА ОДНИМ И ТЕМ ЖЕ КОЛИЧЕСТВОМ ЭЛЕКТРИЧЕСТВА КОНДЕНСАТОРОВ РАЗЛИЧНОЙ ЕМКОСТИ ВСЕГДА ТРЕБУЮТСЯ РАЗЛИЧНЫЕ НАПРЯЖЕНИЯ. ЧЕМ МЕНЬШЕ ЕМКОСТЬ КОНДЕНСАТОРА, ТЕМ БОЛЬШЕЕ НАПРЯЖЕНИЕ НЕОБХОДИМО ДЛЯ ТОГО, ЧТОБЫ ЗАРЯДИТЬ ЭТОТ КОНДЕНСАТОР ТРЕБУЕМЫМ КОЛИЧЕСТВОМ ЭЛЕКТРИЧЕСТВА, И НАОБОРОТ.

ТАКИМ ОБРАЗОМ, ПРИ ЗАРЯДЕ ГРУППЫ КОНДЕНСАТОРОВ, СОЕДИНЕННЫХ ПОСЛЕДОВАТЕЛЬНО, НА КОНДЕНСАТОРАХ МАЛОЙ ЕМКОСТИ НАПРЯЖЕНИЯ БУДУТ БОЛЬШЕ, А НА КОНДЕНСАТОРАХ БОЛЬШОЙ ЕМКОСТИ — МЕНЬШЕ.
АНАЛОГИЧНО ПРЕДЫДУЩЕМУ СЛУЧАЮ МОЖНО РАССМАТРИВАТЬ ВСЮ ГРУППУ КОНДЕНСАТОРОВ, СОЕДИНЕННЫХ ПОСЛЕДОВАТЕЛЬНО, КАК ОДИН ЭКВИВАЛЕНТНЫЙ КОНДЕНСАТОР, МЕЖДУ ПЛАСТИНАМИ КОТОРОГО СУЩЕСТВУЕТ НАПРЯЖЕНИЕ, РАВНОЕ СУММЕ НАПРЯЖЕНИЙ НА ВСЕХ КОНДЕНСАТОРАХ ГРУППЫ, А ЗАРЯД КОТОРОГО РАВЕН ЗАРЯДУ ЛЮБОГО ИЗ КОНДЕНСАТОРОВ ГРУППЫ.
ВОЗЬМЕМ САМЫЙ МАЛЕНЬКИЙ КОНДЕНСАТОР В ГРУППЕ. НА НЕМ ДОЛЖНО БЫТЬ САМОЕ БОЛЬШОЕ НАПРЯЖЕНИЕ. НО НАПРЯЖЕНИЕ НА ЭТОМ КОНДЕНСАТОРЕ СОСТАВЛЯЕТ ТОЛЬКО ЧАСТЬ ОБЩЕГО НАПРЯЖЕ­НИЯ, СУЩЕСТВУЮЩЕГО НА ВСЕЙ ГРУППЕ КОНДЕНСАТОРОВ. НАПРЯ­ЖЕНИЕ НА ВСЕЙ ГРУППЕ БОЛЬШЕ НАПРЯЖЕНИЯ НА КОНДЕНСАТОРЕ, ИМЕЮЩЕМ САМУЮ МАЛУЮ ЕМКОСТЬ. А ОТСЮДА НЕПОСРЕДСТВЕННО СЛЕДУЕТ, ЧТО ОБЩАЯ ЕМКОСТЬ ГРУППЫ КОНДЕНСАТОРОВ, СОЕДИНЕН­НЫХ ПОСЛЕДОВАТЕЛЬНО, МЕНЬШЕ ЕМКОСТИ САМОГО МАЛОГО КОНДЕН­САТОРА В ГРУППЕ.

ДЛЯ ВЫЧИСЛЕНИЯ ОБЩЕЙ ЕМКОСТИ ПРИ ПОСЛЕДОВАТЕЛЬНОМ СО­ЕДИНЕНИИ КОНДЕНСАТОРОВ УДОБНЕЕ ВСЕГО ПОЛЬЗОВАТЬСЯ СЛЕДУЮ­ЩЕЙ ФОРМУЛОЙ:
ДЛЯ ЧАСТНОГО СЛУЧАЯ ДВУХ ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ КОНДЕНСАТОРОВ ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ ИХ ОБЩЕЙ ЕМКОСТИ БУДЕТ ИМЕТЬ ВИД:

ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОЕ (СМЕШАННОЕ) СОЕДИНЕНИЕ КОНДЕНСАТОРОВ
ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ КОНДЕНСАТОРОВ НАЗЫВАЕТСЯ ЦЕПЬ ИМЕЮЩАЯ В СВОЕМ СОСТАВЕ УЧАСТКИ, КАК С ПАРАЛЛЕЛЬНЫМ, ТАК И С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ КОНДЕНСАТОРОВ.
НА РИСУНКЕ 4 ПРИВЕДЕН ПРИМЕР УЧАСТКА ЦЕПИ СО СМЕШАННЫМ СОЕДИНЕНИЕМ КОНДЕНСАТОРОВ.