Содержание
- 2. ЛЕКЦИЯ № 3 1. Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов. 2.
- 3. Работа сил электростатического поля при перемещении заряда. Потенциал. Рассмотрим произвольное перемещение (1–а–2) заряда q в электростатическом
- 4. Вычислим работу кулоновской силы при перемещении заряда q из точки 1 в положение 2 (по любой
- 5. Величина работы никак не связана с видом траектории. Она зависит только от положения её начальной (r1)
- 6. Потенциальная энергия системы двух точечных зарядов, или, что то же самое, энергия заряда q в электрическом
- 7. Потенциальная энергия заряженной частицы в электрическом поле зависит, таким образом, от величины заряда q и от
- 8. Можно придать потенциалу и иной физический смысл. Поместим заряд q в поле точечного заряда Q. Первоначально
- 9. Потенциал некоторой точки электростатического поля равен работе, совершаемой электрической силой при удалении единичного положительного заряда из
- 10. Работа каждой силы равна: Здесь — потенциал поля, создаваемого в точке 1 зарядом Qi. Таким образом,
- 11. Разность потенциалов. Обратимся к вычислению работы электрической силы при перемещении заряда q из точки 1 теперь
- 12. или: Здесь — разность потенциалов двух точек поля. Разность потенциалов равна работе, совершаемой электрической силой при
- 13. Зная разность потенциалов двух точек поля, легко вычислить работу электрического поля, совершаемую при перемещении заряда q
- 14. Теорема о циркуляции вектора напряжённости электростатического поля Существуют два равнозначных определения консервативной силы. Оба они подробно
- 15. Рассмотрим перемещение заряда q в электростатическом поле по замкнутой траектории. Заряд из точки 1 перемещается по
- 16. Связь напряжённости и потенциала электростатического поля Для отыскания связи, вычислим работу электрической силы на элементарном перемещении
- 17. Здесь El — проекция вектора напряжённости поля на направление перемещения, а — изменение потенциала при переходе
- 18. Полный вектор напряжённости можно представить в виде векторной суммы: Последнее уравнение принято записывать так: Здесь векторный
- 19. Последнее уравнение устанавливает искомую связь двух характеристик электростатического поля — напряжённости и потенциала: напряжённость электростатического поля
- 20. Формула выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в
- 21. Эквипотенциальные поверхности Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности
- 23. Скачать презентацию




















 Удельная теплоёмкость
Удельная теплоёмкость Квантовые свойства электромагнитного излучения
Квантовые свойства электромагнитного излучения Молекулярная физика. Основные положения МКТ
Молекулярная физика. Основные положения МКТ Урок 21+ Розв'язування задач
Урок 21+ Розв'язування задач Предыстория радиотехники. Лекция 3
Предыстория радиотехники. Лекция 3 Изучение хроматографической подвижности
Изучение хроматографической подвижности Радиационное и электромагнитное излучение
Радиационное и электромагнитное излучение Расчет сопротивления проводника. Удельное сопротивление. 24.02.2012г.
Расчет сопротивления проводника. Удельное сопротивление. 24.02.2012г. Механика деформируемого твердого тела
Механика деформируемого твердого тела Презентация по физике "Работа электростатического поля по перемещению заряда" -
Презентация по физике "Работа электростатического поля по перемещению заряда" -  Контрольная работа №1, часть 2. Механические колебания. Вариант 999
Контрольная работа №1, часть 2. Механические колебания. Вариант 999 Механическая работа и мощность
Механическая работа и мощность Марковские процессы
Марковские процессы Действие электрического тока на человека Урок по физике 8 класс Учителя МОУ СОШ №1 г.Миньяра Лактионовой Надежды Сергеевны
Действие электрического тока на человека Урок по физике 8 класс Учителя МОУ СОШ №1 г.Миньяра Лактионовой Надежды Сергеевны Соединение обмоток генератора треугольником
Соединение обмоток генератора треугольником Выпуск первого автомобиля в г. Тольятти
Выпуск первого автомобиля в г. Тольятти Изобретение радио Александром Степановичем Поповым
Изобретение радио Александром Степановичем Поповым Неразъёмные соединения. (Лекция 4)
Неразъёмные соединения. (Лекция 4) Измерение линейных и угловых размеров деталей оптическими средствами
Измерение линейных и угловых размеров деталей оптическими средствами Метод наложения для расчета электрических цепей
Метод наложения для расчета электрических цепей Криволинейное движение. Равномерное движение материальной точки по окружности. Линейная и угловая скорости
Криволинейное движение. Равномерное движение материальной точки по окружности. Линейная и угловая скорости Сила упругости
Сила упругости Двухмасовый маховик
Двухмасовый маховик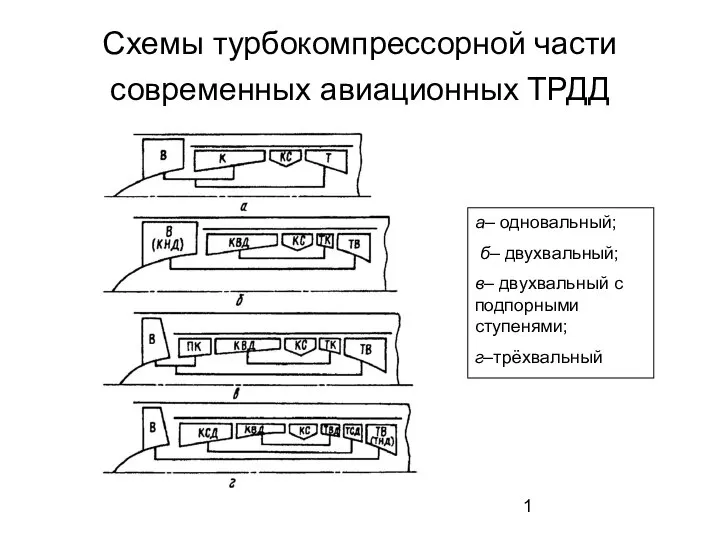 Конвертированные двигатели. Схемы турбокомпрессорной части современных авиационных ТРДД
Конвертированные двигатели. Схемы турбокомпрессорной части современных авиационных ТРДД Принципи на механиката. Задачи. 8 клас
Принципи на механиката. Задачи. 8 клас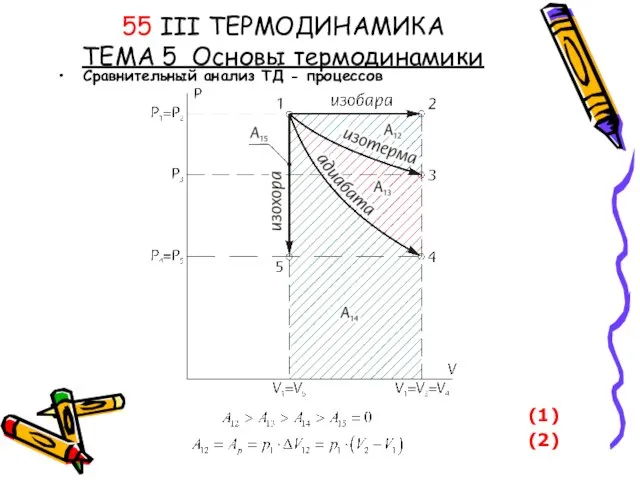 55 III ТЕРМОДИНАМИКА ТЕМА 5 Основы термодинамики Сравнительный анализ ТД - процессов
55 III ТЕРМОДИНАМИКА ТЕМА 5 Основы термодинамики Сравнительный анализ ТД - процессов Инструменты, механизмы и технические устройства
Инструменты, механизмы и технические устройства Стенд для лабораторных работ Зубчатые передачи
Стенд для лабораторных работ Зубчатые передачи