Содержание
- 2. I.Механика. Консервативные силы. энергии). В случае действия нескольких сил, сила F есть их равнодействующая. Потенциальная энергия
- 3. I.Механика. Консервативные силы. Потенциальная энергия. а 1 2 b Рис.11 При изменении направления перемещения знак работы
- 4. I.Механика. Консервативные силы. Потенциальная энергия. В поле консервативных сил можно ввести потенциальную энергию, определив ее как
- 5. I.Механика. Консервативные силы. Потенциальная энергия. Тогда сила связана с потенциальной энергией следующим соотношением , где Градиент
- 6. I.Механика. Закон сохранения энергии При рассмотрении механической системы необходимо учитывать силы взаимодействия между ее материальными точками.
- 7. I.Механика. Метод Потенциальных кривых механической системы сохраняется. Системы в которых действуют только консервативные силы (как внутренние,
- 8. I.Механика. Метод Потенциальных кривых отрицательна. Слева от минимума тангенс угла наклона касательной отрицателен, а сила положительна.
- 9. I.Механика. Неупругий и упругий удары. Пусть два тела движутся вдоль прямой, соединяющей их центры, а после
- 10. I.Механика. Неупругий и упругий удары. первому телу, а справа ко второму. Разделив первое уравнение на второе,
- 11. I.Механика. Неупругий и упругий удары. 0,5 кг, движение под действием которой происходит по закону: x =
- 12. I.Механика. Неупругий и упругий удары. Работа на бесконечно малом отрезке оси x равна dA=Fx dx, а
- 13. I.Механика. Неупругий и упругий удары. Решение. Запишем законы сохранения энергии и импульса для неупругого удара: где
- 14. I.Механика. Неупругий и упругий удары. Задача 27. Шар массой 3m, движущийся со скоростью = 10 м/с,
- 15. I.Механика. Неупругий и упругий удары. Разделив второе уравнение на первое, получим и система уравнений примет вид:
- 16. I.Механика. Неупругий и упругий удары. Задача 29. Частица находится в центральном поле сил, где ее потенциальная
- 18. Скачать презентацию















 Пример планового техобслуживания автомобиля
Пример планового техобслуживания автомобиля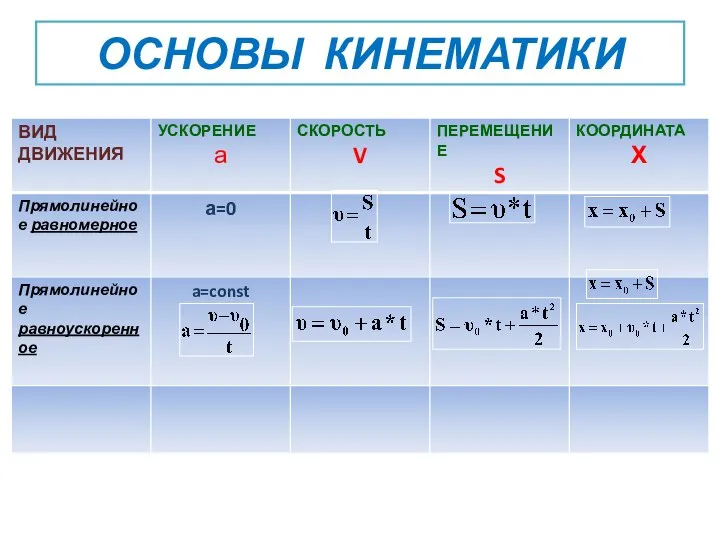 Основы кинематики
Основы кинематики Презентация на тему Виды спектров. Спектральный анализ
Презентация на тему Виды спектров. Спектральный анализ  ВСР№14. Распространение механических колебаний в упругих средах. Поперечные и продольные волны. Звук и ультразвук
ВСР№14. Распространение механических колебаний в упругих средах. Поперечные и продольные волны. Звук и ультразвук Сборка электрической цепи и измерение силы тока в ее различных участках
Сборка электрической цепи и измерение силы тока в ее различных участках Игра-КВН Первый урок в 8 классе
Игра-КВН Первый урок в 8 классе Силы в механике
Силы в механике I закон термодинамики
I закон термодинамики 4. Основы МКТ
4. Основы МКТ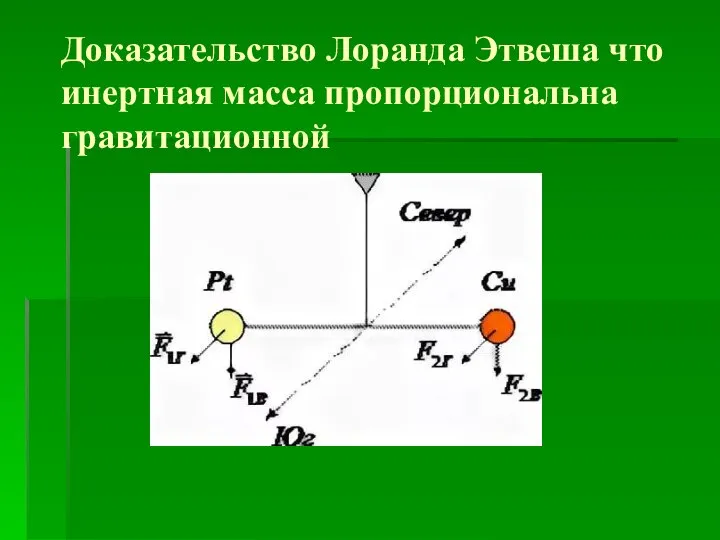 Доказательство Лоранда Этвеша что инертная масса пропорциональна гравитационной
Доказательство Лоранда Этвеша что инертная масса пропорциональна гравитационной Плоские электромагнитные волны в средах с потерями
Плоские электромагнитные волны в средах с потерями Электрические машины
Электрические машины Термодинамика негіздері
Термодинамика негіздері Презентация на тему Испарение и конденсация
Презентация на тему Испарение и конденсация  Техническая механика. Срез, смятие, расчетные формулы
Техническая механика. Срез, смятие, расчетные формулы Тепловое излучение
Тепловое излучение Что? Где? Когда? Исаак Ньютон
Что? Где? Когда? Исаак Ньютон Презентация на тему Электрический ток
Презентация на тему Электрический ток  3_ЭМКолебания
3_ЭМКолебания Повышение экологичности автомобиля УРАЛ-4420 применением системы насыщения воздуха активными добавками на впуске в двигатель
Повышение экологичности автомобиля УРАЛ-4420 применением системы насыщения воздуха активными добавками на впуске в двигатель Закон Ома. Сопротивление цепи
Закон Ома. Сопротивление цепи Обоснование состава и разработка структуры инерциальной навигационной системы легкового автомобиля
Обоснование состава и разработка структуры инерциальной навигационной системы легкового автомобиля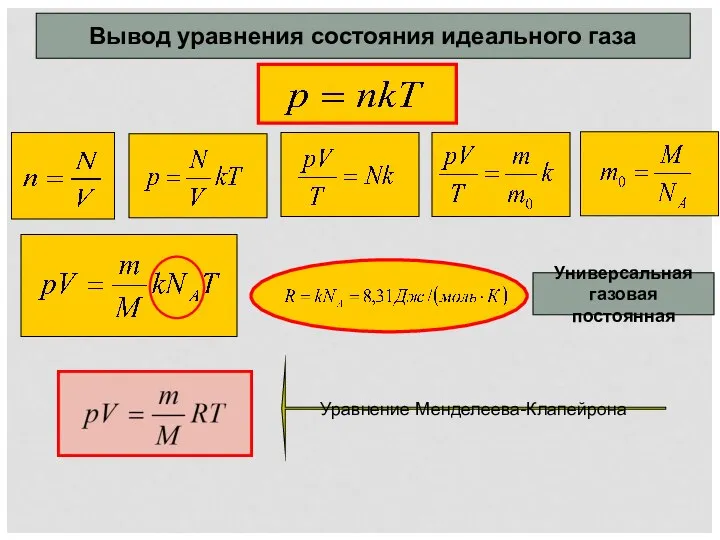 Вывод уравнения Менделеева-Клайперона. Изопроцессы
Вывод уравнения Менделеева-Клайперона. Изопроцессы Источники звука. Звуковые волны
Источники звука. Звуковые волны Газовые законы
Газовые законы УФ-спектроскопия. Часть 1
УФ-спектроскопия. Часть 1 Расчет измерительных преобразователей
Расчет измерительных преобразователей УСТРОЙСТВО Л.Л
УСТРОЙСТВО Л.Л