Естественный способ задания движения

▼
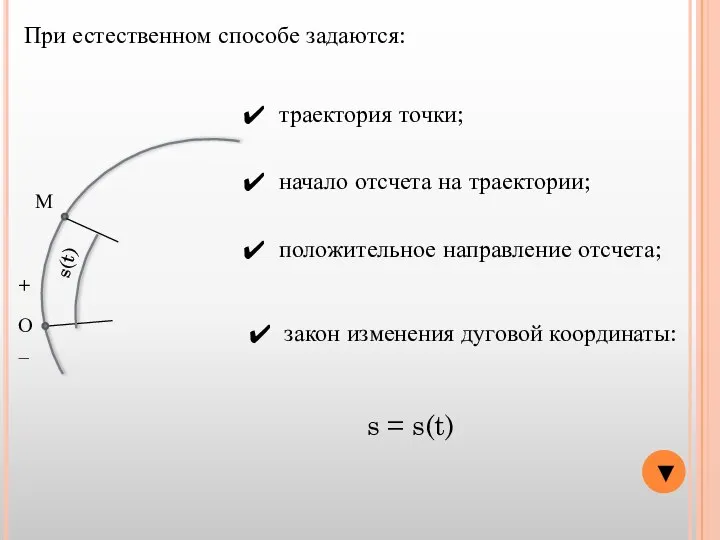
При естественном способе задаются:
траектория точки;
начало отсчета на траектории;
положительное направление отсчета;
закон изменения дуговой координаты:
s = s(t)
О
−
+
М
s(t)

▼
О
−
+
М
s
Определение скорости точки
М1
s1
Δs
Пусть за время t точка прошла путь ОМ = s.
За время t1 = t + Δt точка прошла путь ОМ1 = s1.
Δ s – путь, пройденный точкой за время Δt.

Отношении пройденного пути Δs к промежутку времени Δt называется средней скоростью точки за время Δt.
Скорость точки в данный момент времени находится как предел средней скорости при стремлении промежутка времени к нулю, то есть
▼

М
▼
Следовательно,
Алгебраическое значение скорости в данный момент времени равно производной от дуговой координаты по времени.
Вектор скорости направлен по касательной к траектории точки в сторону движения.

▼
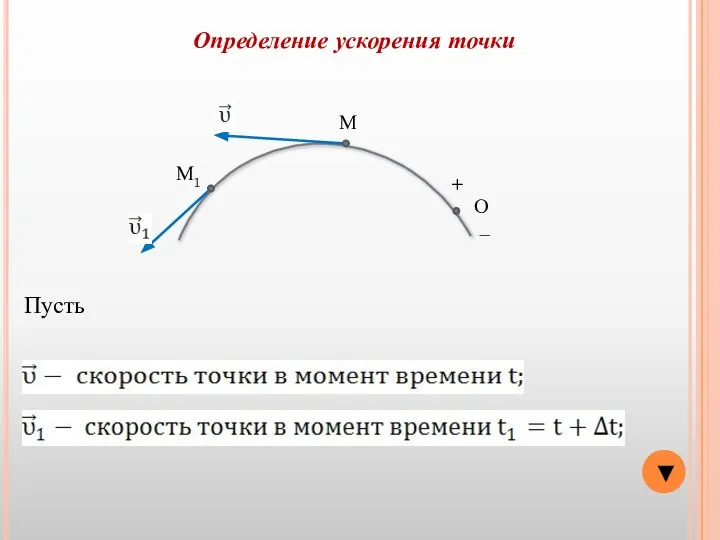
О
−
+
М
Определение ускорения точки
М1
Пусть

▼
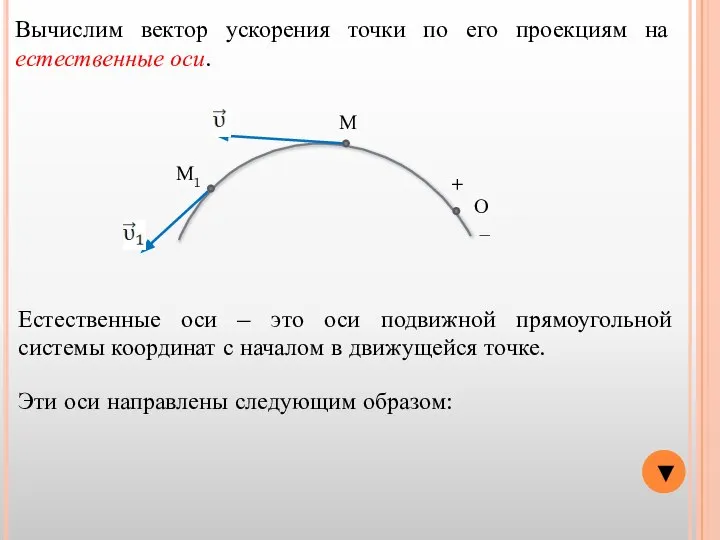
О
−
+
М
М1
Вычислим вектор ускорения точки по его проекциям на естественные оси.
Естественные оси – это оси подвижной прямоугольной системы координат с началом в движущейся точке.
Эти оси направлены следующим образом:

▼
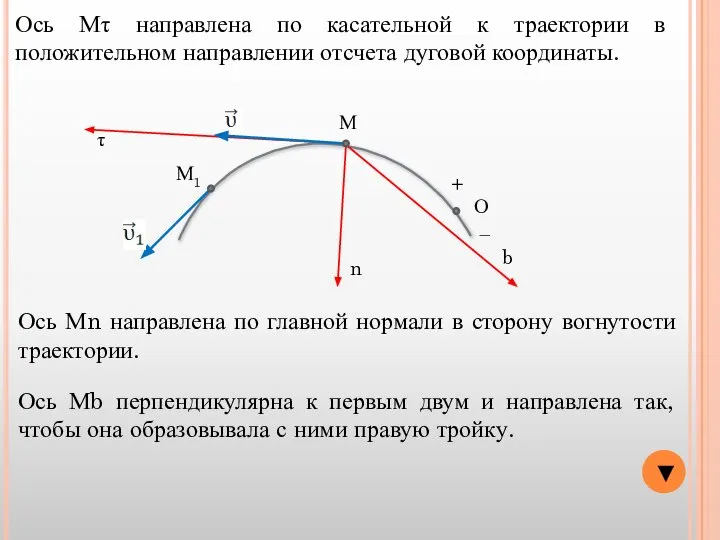
О
−
+
М
М1
Ось Мτ направлена по касательной к траектории в положительном направлении отсчета дуговой координаты.
τ
Ось Мn направлена по главной нормали в сторону вогнутости траектории.
n
Ось Мb перпендикулярна к первым двум и направлена так, чтобы она образовывала с ними правую тройку.
b

▼
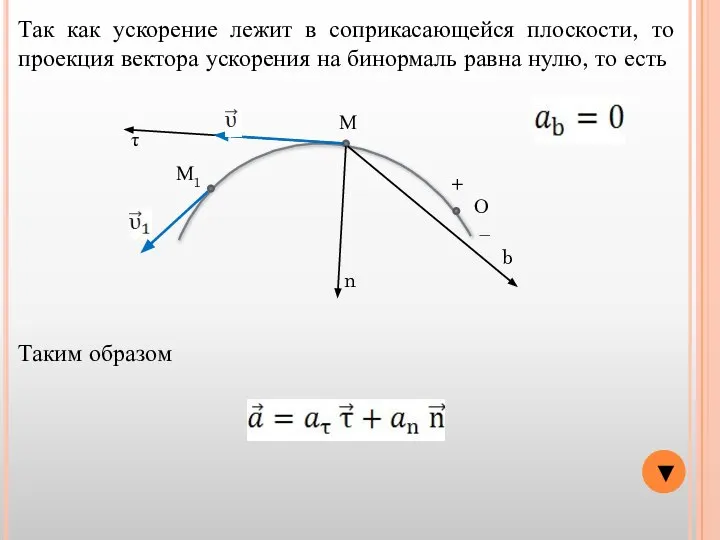
О
−
+
М
М1
Так как ускорение лежит в соприкасающейся плоскости, то проекция вектора ускорения на бинормаль равна нулю, то есть
τ
n
b
Таким образом

▼
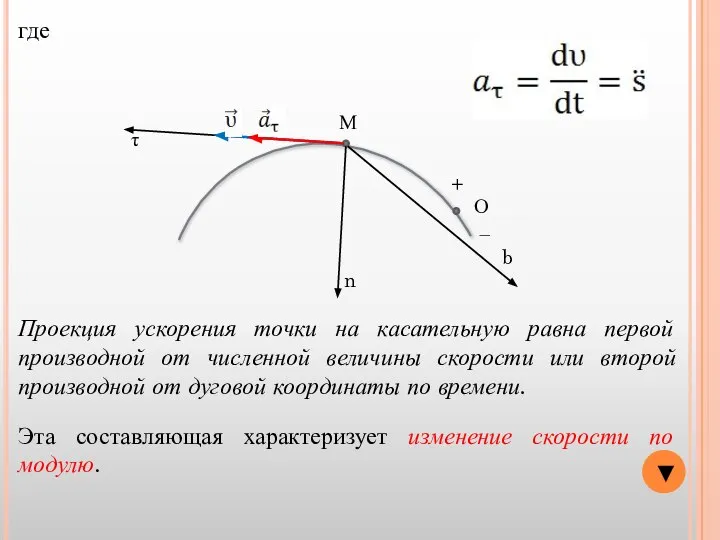
О
−
+
М
τ
n
b
где
Проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от дуговой координаты по времени.
Эта составляющая характеризует изменение скорости по модулю.

▼
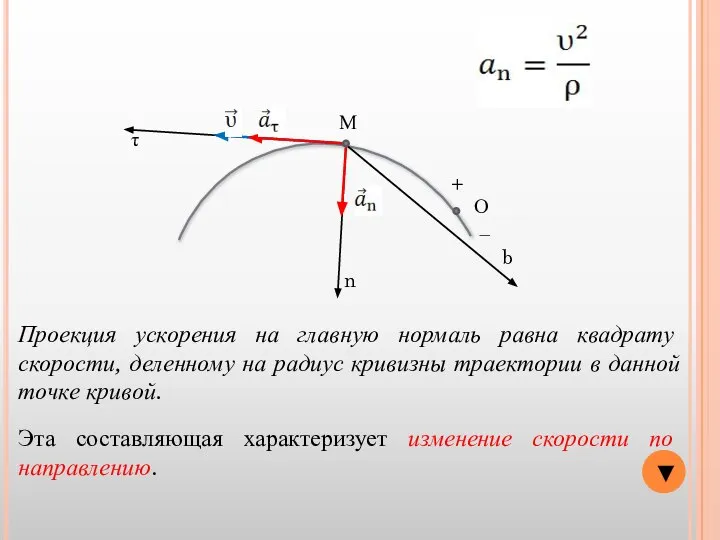
О
−
+
М
τ
n
b
Проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой.
Эта составляющая характеризует изменение скорости по направлению.