Физика

(Элементарная)
ФИЗИКА
(для ПриМатов и Программистов)

Физика (от греч. φύσις (physis) - природа) – это наука, изучающая простейшие и вместе с тем наиболее общие свойства и законы движения (взаимодействия) окружающих нас объектов материального мира.
Задачи и методы физики
Задача физики состоит в создании в нашем сознании такой модельной картины физического мира, которая наиболее полно отражает его свойства.
Физика – наука экспериментальная. Экспериментальный метод физики состоит в следующем: на основе экспериментов и наблюдений создается модель, в рамках которой делаются предсказания о явлениях, проверяемых в свою очередь в экспериментах и наблюдениях. В результате этого уточняется модель, и делаются новые предсказания.
Галилео Галилей
(1564–1642))
Аристотель
(384-322 гг. до н.э))

Лекция 1
Механика:
Кинематика материальной точки
Кинематика (от греческого слова kinema – движение) – раздел механики, в котором изучаются геометрические свойства движения тел без учета их массы и действующих на них сил.

Модель – абстрактная система, являющаяся упрощенной копией реальной системы.
Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи.
Движение тел происходит в пространстве и времени
Следовательно, для описания движения материальной точки надо знать, в каких местах пространства эта точка находится в различные моменты времени.

Положение материальной точки
определяется по отношению к какому-либо другому произвольно выбранному телу.
Всякое движение относительно, поэтому для описания движения необходимо условиться, относительно какого другого тела будет отсчитываться перемещение данного тела. Выбранное для этой цели тело называют телом отсчета.
Тело отсчета – реальный объект.
С телом отсчета связывают систему координат – это абстракция (декартова, сферическая, цилиндрическая системы координат).

Приборы, служащие для определения положения движущегося тела – линейка и т.п.
Прибор, служащий для определения времени – часы – любой периодический процесс.
Если есть несколько тел и, соответственно, несколько часов, то необходимы приборы для синхронизации часов.

Тело отсчета, связанная с ним система координат, линейка, часы и приборы для синхронизации часов составляют пространственно-временную систему отсчета (СО).
Гелиоцентрическая СО – тело отсчета Солнце.
Геоцентрическая СО – тела отсчета Земля.

В кинематике решаются две основные задачи: прямая и обратная.
При решении прямой задачи по известному закону движения
находятся все остальные кинематические характеристики материальной точки:
путь, перемещение, скорость и ускорение в любой момент времени.
При решении обратной задачи по известной зависимости ускорения от времени ,
находят положение материальной точки на траектории в любой момент времени. Для решения обратной задачи нужно задать в некоторый начальный момент времени t0 начальные условия: радиус-вектор и начальную скорость

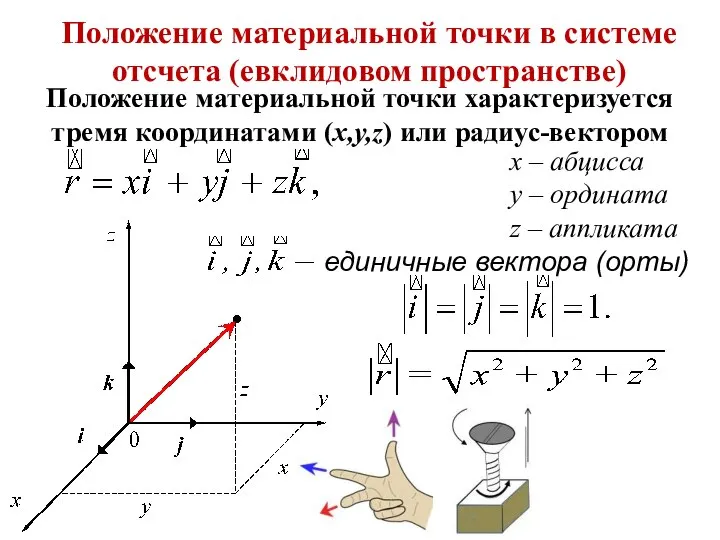
Положение материальной точки характеризуется тремя координатами (x,y,z) или радиус-вектором
единичные вектора (орты)
x – абцисса
y – ордината
z – аппликата
Положение материальной точки в системе отсчета (евклидовом пространстве)

Движение материальной точки определяется системой скалярных уравнениями
или векторным уравнением
Эти уравнения называются кинематическими уравнениями движения материальной точки.
Закон движения – это уравнение, определяющее положение тела в пространстве в любой момент времени (Основная задача механики).

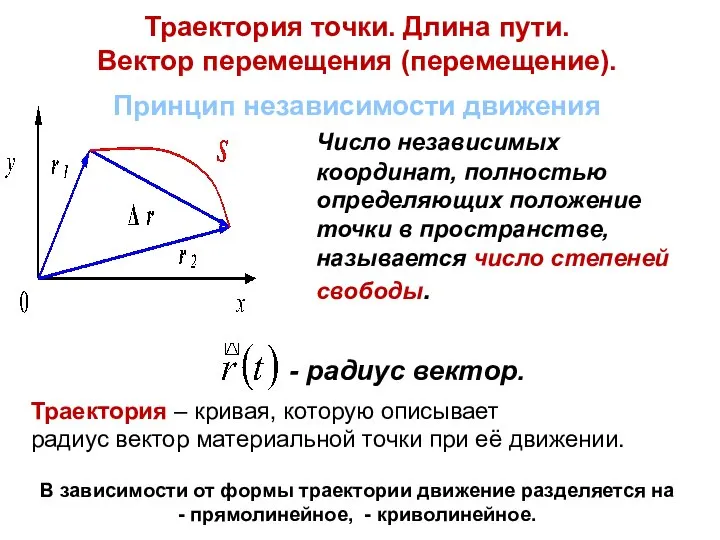
Траектория точки. Длина пути.
Вектор перемещения (перемещение).
Принцип независимости движения
Число независимых координат, полностью определяющих положение точки в пространстве, называется число степеней свободы.
- радиус вектор.
Траектория – кривая, которую описывает
радиус вектор материальной точки при её движении.
В зависимости от формы траектории движение разделяется на
- прямолинейное, - криволинейное.

Расстояние, отсчитанное вдоль траектории, (длина участка траектории) называется длиной пути S.
- скалярная функция.
Направленный отрезок прямой (вектор), соединяющий начальную и конечную точки траектории называется вектором перемещения (перемещением).

При прямолинейном движении
Если движение происходит в течение бесконечно малого времени Δt → 0, то по модулю путь равен перемещению
.

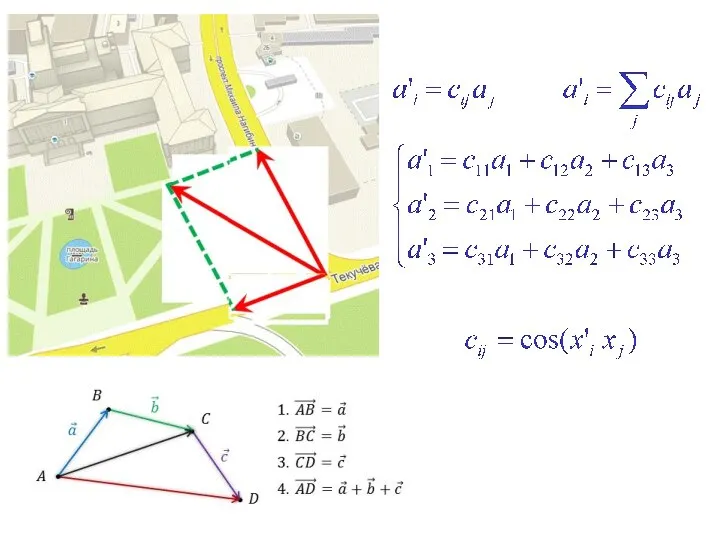
Если материальная точка участвует в нескольких перемещениях, то результирующее перемещение равно векторной сумме перемещений, совершаемых материальной точкой в каждом из движений в отдельности:
Принцип суперпозиции играет большую роль во многих разделах физики и техники!

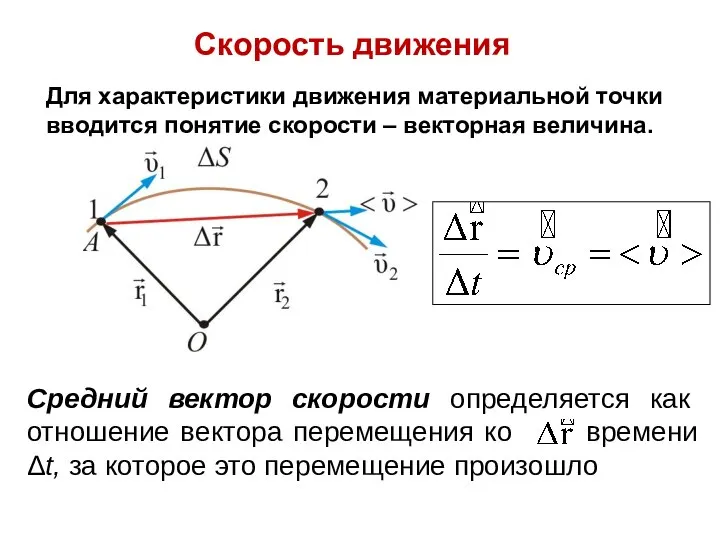
Скорость движения
Для характеристики движения материальной точки
вводится понятие скорости – векторная величина.
Средний вектор скорости определяется как отношение вектора перемещения ко времени Δt, за которое это перемещение произошло

Мгновенная скорость материальной точки
– векторная величина, равная первой производной радиус-вектора движущейся точки по времени.
, следовательно, модуль мгновенной скорости равен первой производной пути по времени:

В математике производной функции
в точке x0 называется предел отношения изменения функции Δy в этой точке к вызвавшему его изменению аргумента Δx при произвольном стремлении Δx к нулю
Исаак Ньютон
(1643 – 1727)
Готфрид Лейбниц
(1646 — 1716)

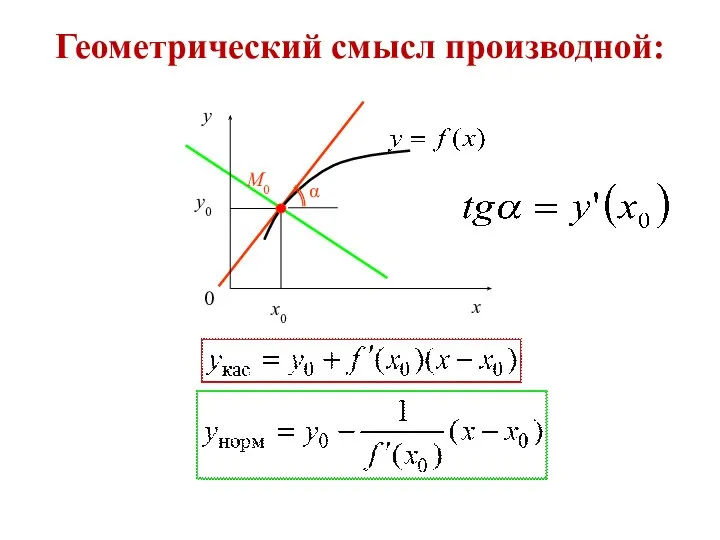
Геометрический смысл производной:
α

Физический смысл производной:
это среднее значение изменения функции на таком интервале, на котором среднее значение функции не меняется.
Мгновенная скорость
– проекции
вектора скорости
на оси координат.

Неравномерное движение
Средняя скорость неравномерного движения – скалярная величина.
Средняя скорость больше модуля вектора средней скорости.

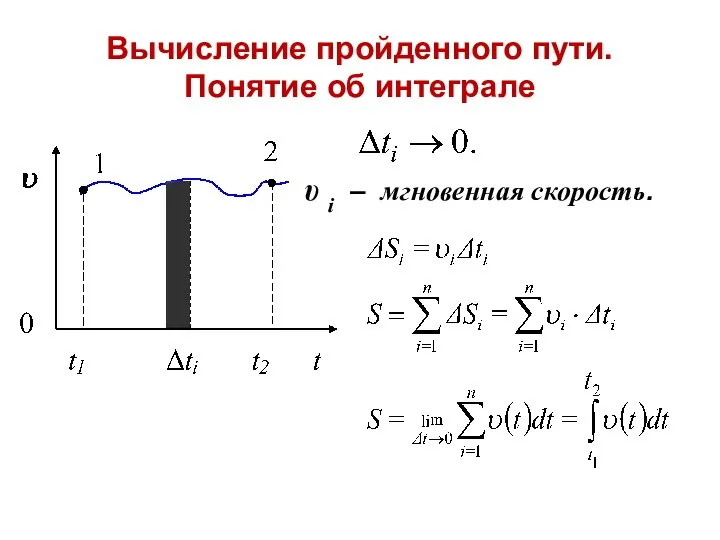
Вычисление пройденного пути.
Понятие об интеграле
υ i – мгновенная скорость.

Физический смысл интеграла –
бесконечно большая сумма бесконечно
малых слагаемых.
Геометрический смысл интеграла –
площадь под кривой, ограниченная двумя
перпендикулярами и осью абсцисс.

Средняя скорость прохождения пути
Средняя скорость неравномерного движения – средняя скорость такого равномерного движения, при котором материальная точка за то же время проходит тот же путь.

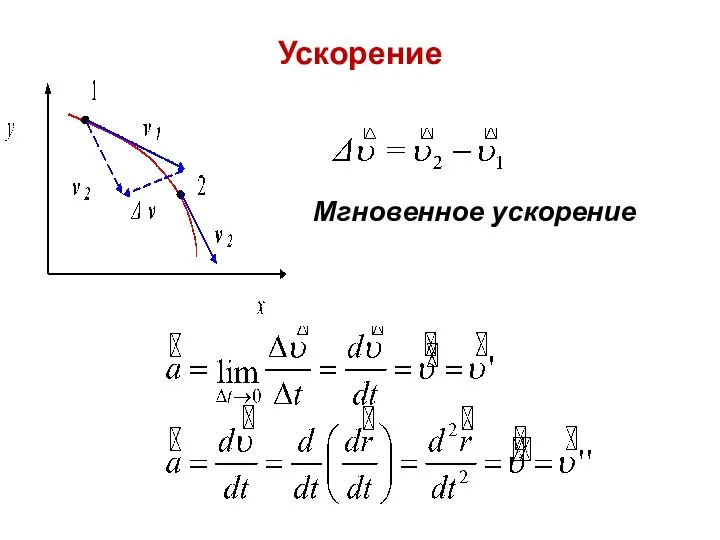
Ускорение
Мгновенное ускорение

Модуль среднего ускорения:
Ускорение движения материальной точки это первая производная от вектора скорости по времени или вторая производная от радиус-вектора по времени.
– проекции вектора ускорения на координатные оси.

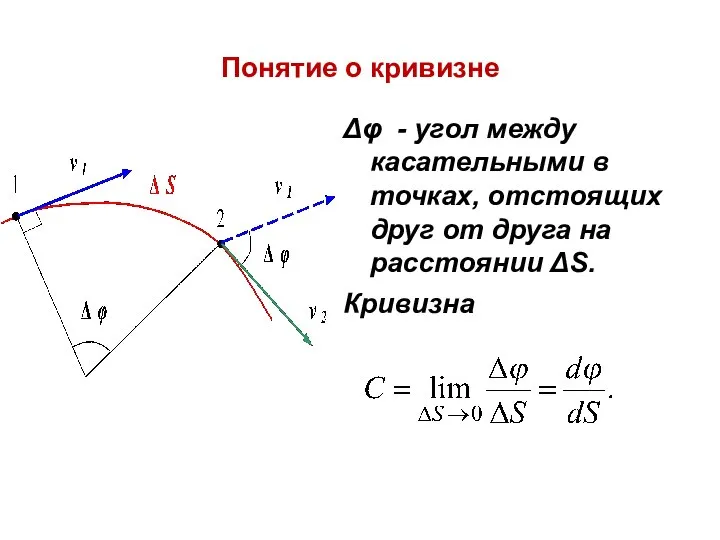
Понятие о кривизне
Δφ - угол между касательными в точках, отстоящих друг от друга на расстоянии ΔS.
Кривизна

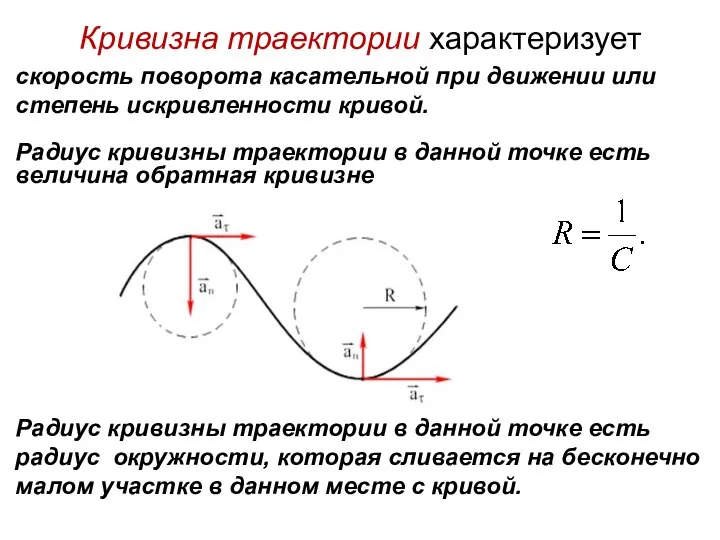
Кривизна траектории характеризует
скорость поворота касательной при движении или степень искривленности кривой.
Радиус кривизны траектории в данной точке есть величина обратная кривизне
Радиус кривизны траектории в данной точке есть радиус окружности, которая сливается на бесконечно малом участке в данном месте с кривой.

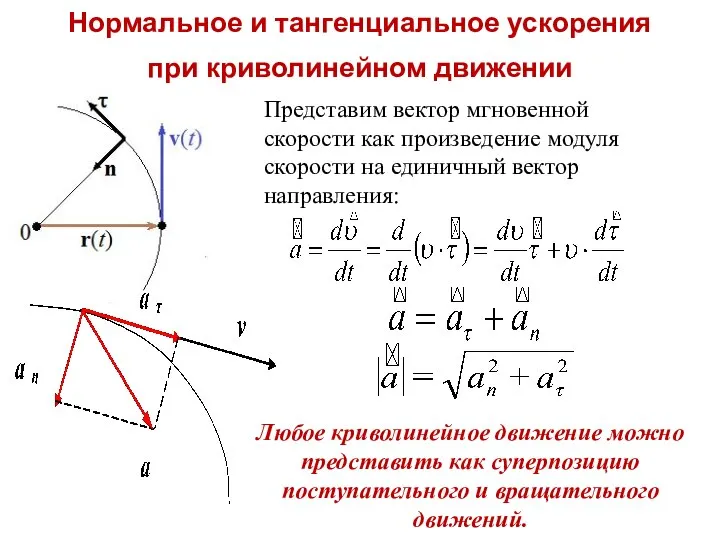
Нормальное и тангенциальное ускорения
при криволинейном движении
Представим вектор мгновенной скорости как произведение модуля скорости на единичный вектор направления:
Любое криволинейное движение можно представить как суперпозицию поступательного и вращательного движений.

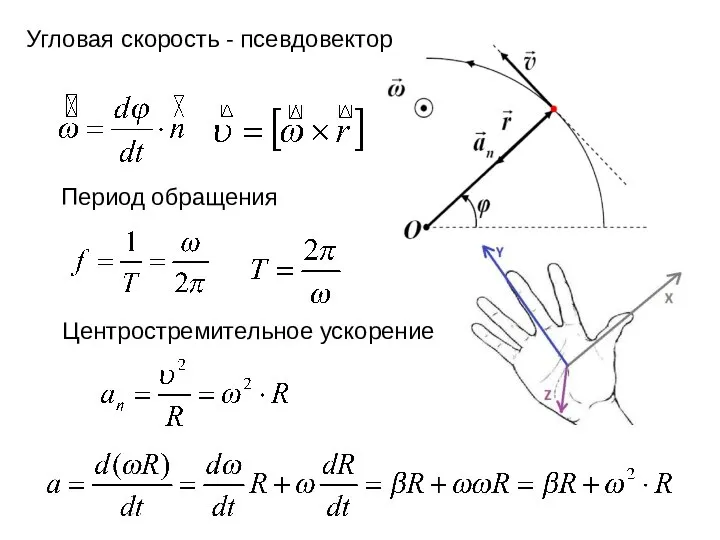
Угловая скорость - псевдовектор
Период обращения
Частота вращения
Центростремительное ускорение

Относительность движения.
Закон сложения скоростей.
Классический нерелятивистский случай
Принцип относительности Галилея

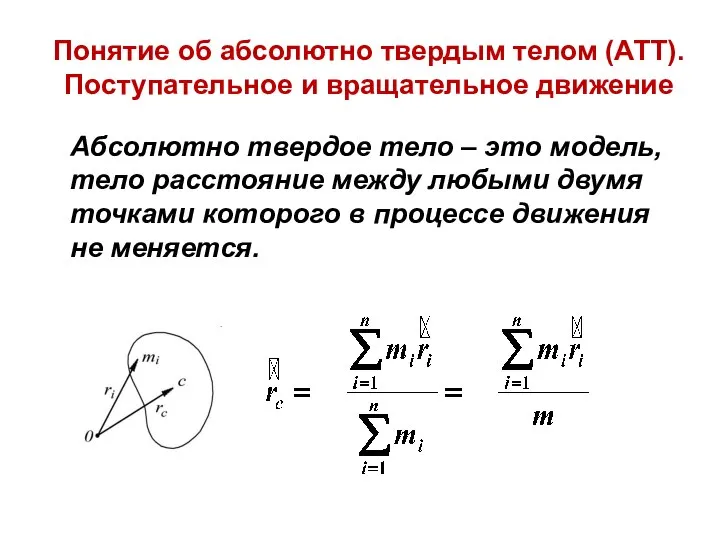
Понятие об абсолютно твердым телом (АТТ).
Поступательное и вращательное движение
Абсолютно твердое тело – это модель, тело расстояние между любыми двумя точками которого в процессе движения не меняется.

Поступательное движение – движение,
при котором любая прямая проведенная внутри тела, перемещается параллельно самой себе.
При поступательном движении все точки тела за одно и
тоже время совершают одинаковые перемещения и в
один и тот же момент времени имеют одинаковые
скорости и ускорения.

Абсолютно твердое тело
Поступательное движение АТТ можно рассматривать, как движение материальной точки.

Кинематические уравнения.
1. Равномерное движение материальной точки вдоль оси x.
x0 – начальная координата.

Кинематические уравнения.
2. Равнопеременное движение.

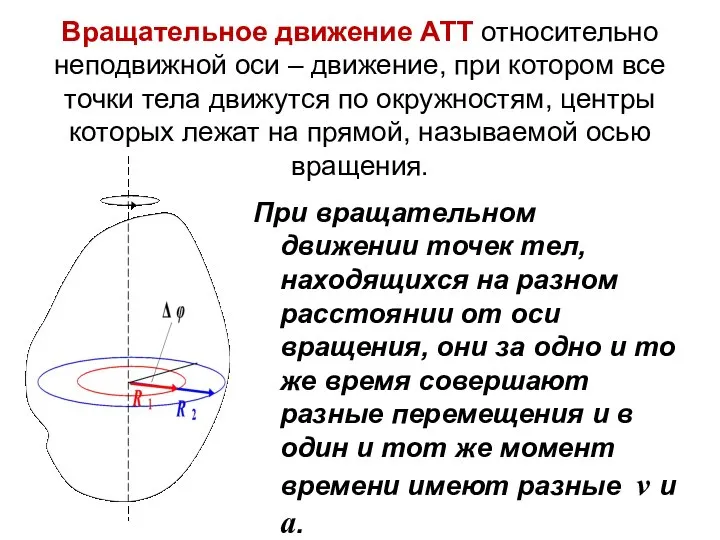
Вращательное движение АТТ относительно неподвижной оси – движение, при котором все точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения.
При вращательном движении точек тел, находящихся на разном расстоянии от оси вращения, они за одно и то же время совершают разные перемещения и в один и тот же момент времени имеют разные v и a.

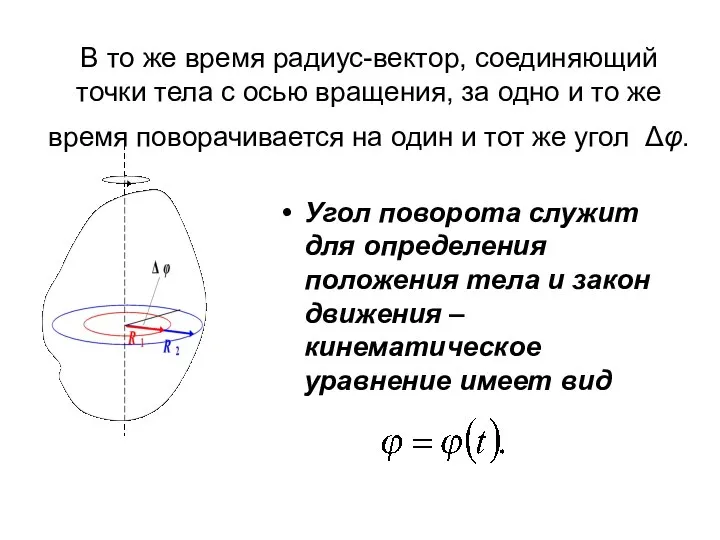
В то же время радиус-вектор, соединяющий точки тела с осью вращения, за одно и то же время поворачивается на один и тот же угол Δφ.
Угол поворота служит для определения положения тела и закон движения – кинематическое уравнение имеет вид

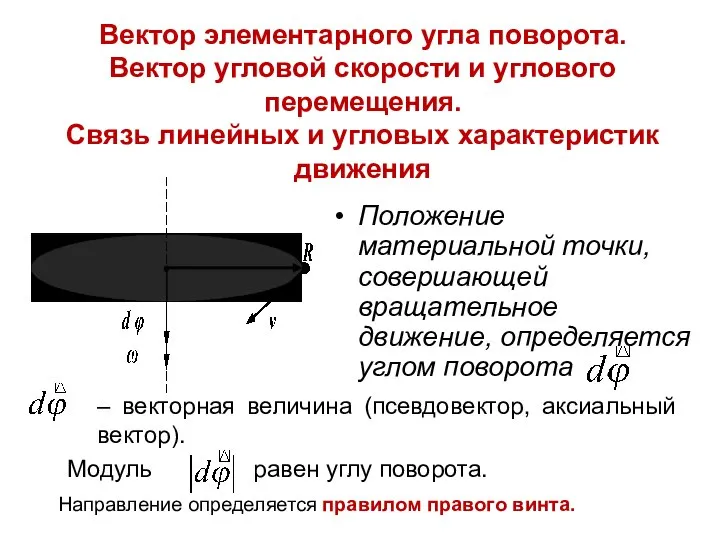
Вектор элементарного угла поворота.
Вектор угловой скорости и углового перемещения.
Связь линейных и угловых характеристик движения
Положение материальной точки, совершающей вращательное движение, определяется углом поворота .
– векторная величина (псевдовектор, аксиальный вектор).
Модуль равен углу поворота.
Направление определяется правилом правого винта.

Угловая скорость
– векторная величина, равная первой производной угла поворота по времени
Линейная скорость точки
В векторном виде

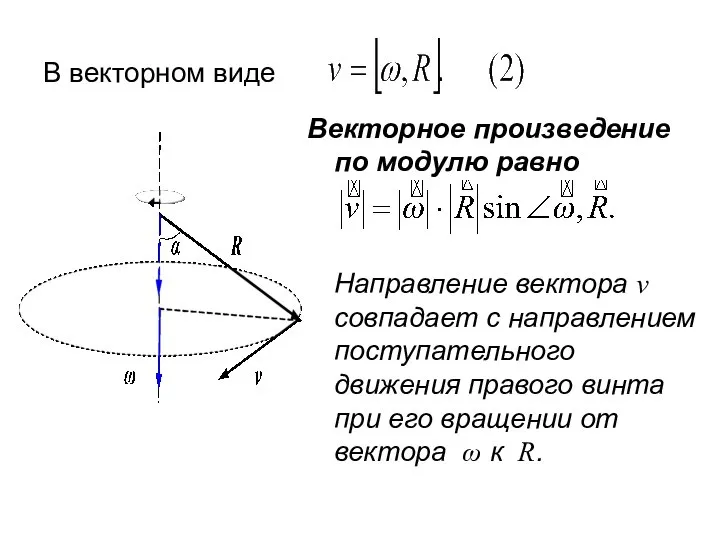
В векторном виде
Векторное произведение по модулю равно
Направление вектора v совпадает с направлением поступательного движения правого винта при его вращении от вектора ω к R.

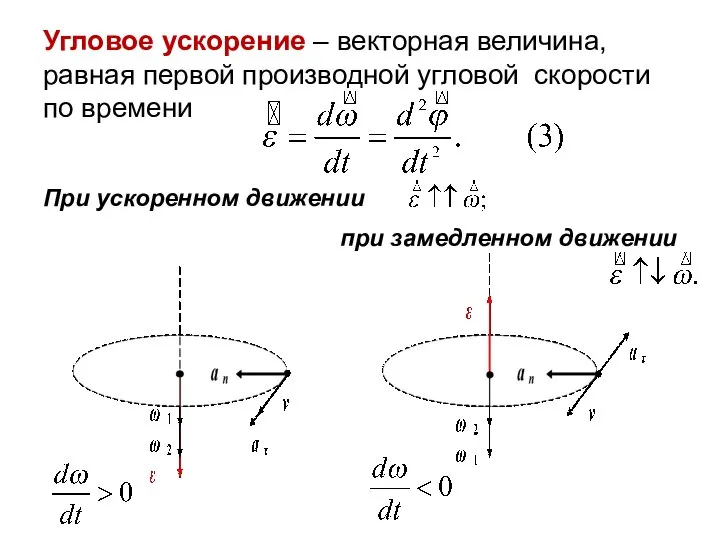
Угловое ускорение – векторная величина, равная первой производной угловой скорости по времени
При ускоренном движении
при замедленном движении

Кинематическое уравнение равномерного вращения
Частота вращения:
Период:

Кинематическое уравнение равнопеременного вращения
Длина пути, пройденного точкой по дуге радиуса R:

Скалярное и векторное произведение векторов
● Скалярное произведение:
Пример: работа, совершаемая силой

● Векторное произведение:
Направление вектора С определяется по правилу правого винта:
1. С перпендикулярен плоскости векторов А, В.
2. Направление вектора С совпадает с направление поступательного движения правого винта при его вращении от А к В.
Другое правило: если наблюдать с конца вектора С, то кратчайший поворот от А до совмещения с В – против часовой стрелки.