Колебания-2. Свободные затухающие колебания, их характеристики. Коэффициент затухания. Логарифмический декремент
Содержание
- 2. Рассмотрим свободные (собственные) затухающие колебания. Система выведена из положения равновесия внешними силами и предоставлена самой себе.
- 3. Продифференцировав по времени получим: Учитывая, Получим: Проинтегрировав: Получим: w вещественна, если w02 > β2, решение уравнения
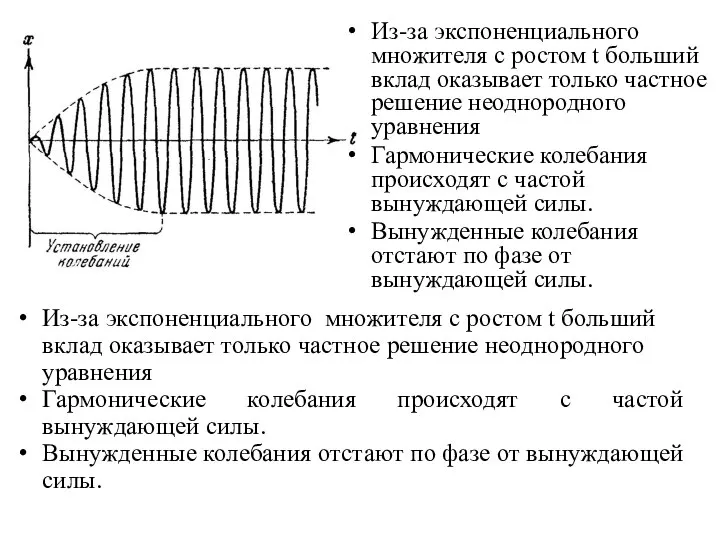
- 4. График функции решения уравнения имеет вид: Амплитуда меняется по гармоническому закону: Скорость затухания колебаний определяется коэффициентом
- 5. Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается
- 6. Вынужденными колебаниями называют колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы-вынуждающей силы.
- 7. (1) (2) (3) Колебание f0coswt- является суммой трёх гармонических колебаний: (1)(2)(3) При этом амплитуда a удовлетворяет
- 8. Из-за экспоненциального множителя с ростом t больший вклад оказывает только частное решение неоднородного уравнения Гармонические колебания
- 10. Скачать презентацию






 Презентация на тему Пластмассы и каучуки
Презентация на тему Пластмассы и каучуки  Невагомiсть
Невагомiсть Магнитные материалы и компоненты. (Лекция 4)
Магнитные материалы и компоненты. (Лекция 4) Физика атома
Физика атома Волновые свойства частиц
Волновые свойства частиц Шкала и первый импульс
Шкала и первый импульс Зонная структура примесных полупроводников. Примесная проводимость. Типы примесных состояний
Зонная структура примесных полупроводников. Примесная проводимость. Типы примесных состояний Презентация на тему Энергия
Презентация на тему Энергия  Свободные и вынужденные электромагнитные колебания
Свободные и вынужденные электромагнитные колебания Презентация на тему Виды излучений
Презентация на тему Виды излучений  Включай смекалку и достигнешь результата! Физика плохому не научит
Включай смекалку и достигнешь результата! Физика плохому не научит Презентация на тему Инерция
Презентация на тему Инерция  Механические колебания. Виды колебаний
Механические колебания. Виды колебаний Презентация на тему Световые кванты
Презентация на тему Световые кванты  Открытие нейтрона
Открытие нейтрона Что и как изучает физика
Что и как изучает физика Тест по теме «Электромагнитные явления» Баскакова Т. И. Учитель физики МОУ ООШ № 48 г. Архангельск
Тест по теме «Электромагнитные явления» Баскакова Т. И. Учитель физики МОУ ООШ № 48 г. Архангельск Простые механизмы
Простые механизмы Движение тел
Движение тел Фотоэффект. Применение фотоэффекта
Фотоэффект. Применение фотоэффекта Спор Альберта Эйнштейна и Нильса Бора
Спор Альберта Эйнштейна и Нильса Бора Презентация на тему Механическая работа и мощность
Презентация на тему Механическая работа и мощность  Электрическое сопротивление. Удельное сопротивление
Электрическое сопротивление. Удельное сопротивление Кипение. Удельная теплота парообразования. Зависимость температуры кипения давления
Кипение. Удельная теплота парообразования. Зависимость температуры кипения давления Свойства внешнего эвольвентного зацепления
Свойства внешнего эвольвентного зацепления Организация технического обслуживания и ремонта автобуса ПАЗ – 3205
Организация технического обслуживания и ремонта автобуса ПАЗ – 3205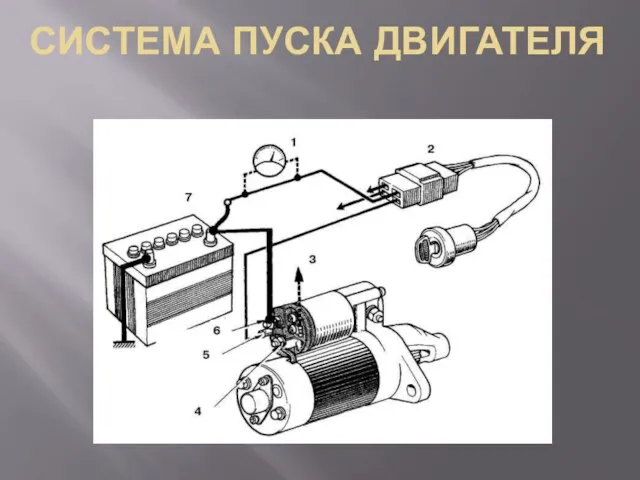 Система пуска двигателя
Система пуска двигателя Лекция 1 Ядерно-топливный цикл
Лекция 1 Ядерно-топливный цикл