ЭКЛ _ЦРС_комп

1.1 Понятие о центральном растяжении и сжатии стержня. Продольная сила
Центральное растяжение (сжатие) – такой вид нагружения стержня, при котором стержень нагружен силами параллельными оси стержня и приложенными в центре тяжести сечения.
Растяжение стержня
Сжатие стержня
Гипотеза Бернулли о плоских сечениях
Поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси в деформированном состоянии; при изгибе сечения поворачиваются не искривляясь.
Принцип Сен-Венана
В сечениях, достаточно удаленных от мест приложения внешней нагрузки, деформация тела не зависит от способа нагружения и определяется только статическим эквивалентом нагрузки.

Жесткие и прочные межатомные связи, соединяющие атомы недеформированного тела, при растяжении создают большие внутренние силы противодействия внешней нагрузке, стремящиеся сохранить тело как единое целое.
Под действием внешних сил частицы (атомы) материала, из которого сделана конструкция, будут перемещаться, и перемещение частиц под нагрузкой будет продолжаться, пока между внешними и внутренними силами не установится равновесие.
При сжатии межатомные расстояния под нагрузкой уменьшаются, межатомные силы отталкивания растут, и конструкция стремится освободиться от запасенной энергии, переведя ее в работу "выскальзывания" атомов из-под нагрузки куда-либо в боковом направлении.
В результате разрушение различных конструктивных элементов происходит по-разному, что определяется материалом конструкции и, главное, формой и пропорциями конструктивных элементов.
Короткие и "толстые" стержни из пластичного материала при сжатии принимают бочкообразную форму ("сплющиваются").
Стержни из более упругого (хрупкого) материала разрушаются с образованием трещины поперек стержня, и обе его части "проскальзывают" друг относительно друга.

Совершенно иначе теряют несущую способность при нагружении сжатием вдоль оси длинные и тонкие элементы конструкции, широко распространенные в самолетостроении.
При сжатии упругое тело (длинный стержень, тонкая пластина, панель) сохраняет начальную (неизогнутую) форму равновесия до некоторого значения сжимающей силы Ркр, называемой критической.
При небольшом превышении критической силы (и, соответственно, критических напряжений σкр) возникают значительные деформации стержня, который не разрушается, а только упруго изгибается и переходит к другой (изогнутой) форме упругого равновесия.
Если при этом не был достигнут "предел упругости", т. е. напряжения в стержне меньше напряжений предела пропорциональности, то при снятии нагрузки стержень возвращается в исходное состояние.
Л. Эйлер показал, что нагрузка, при которой стержень данной длины и площади поперечного сечения теряет устойчивость зависит только от формы поперечного сечения, модуля упругости (жесткости) материала и условий закрепления концов стержня при нагружении.
При дальнейшем увеличении нагрузки изогнутый стержень разрушается. Такой вид потери несущей способности называется общей потерей устойчивости.
При отсутствии общей потери устойчивости (ось тонкостенного элемента конструкции прямолинейна, не деформирована) нагруженная сжатием конструкция может выйти из строя из-за местных деформаций отдельных участков.
Такой вид потери несущей способности называется местной потерей устойчивости.

Продольная сила Nz – это внутреннее усилие; представляет собой равнодействующую элементарных внутренних нормальных сил, равномерно распределенных по площади поперечного сечения.
Для определения продольной силы применяется метод сечений.
В поперечных сечениях стержня при центральном растяжении и сжатии из шести внутренних силовых факторов возникает только один- продольная (осевая) сила Nz
Продольная сила Nz в произвольном поперечном сечении стержня численно равна алгебраической сумме всех действующих внешних сил, приложенных по одну сторону от рассматриваемого поперечного сечения :

ПРАВИЛО ЗНАКОВ:
- если внешняя сила F направлена от рассматриваемого сечения, то ее необходимо подставлять в формулу со знаком «+»
- если внешняя сила F направлена к рассматриваемому сечению, то ее необходимо подставлять в формулу со знаком «-»

3.2 Напряжения в сечениях стержня
Наклонное сечение стержня
Поперечное сечение

Статическая сторона задачи
Продольная сила является равнодействующей
нормальных напряжений.
Напряжение- мера интенсивности внутренних усилий
(определяет степень нагруженности материала)
На основании гипотезы плоских сечений (гипотезы Бернулли) все волокна стержня получают одинаковые относительные удлинения (ε=const)
Геометрическая сторона задачи
Физическая сторона задачи
Нормальные напряжений распределяются по поперечному
сечению равномерно.
Нормальные напряжений прямо пропорциональны
относительной деформации
Поперечное сечение стержня

В поперечных сечениях стержня при центральном растяжении и сжатии возникают нормальные напряжения
где Nz - продольна сила, возникающая в поперечном сечении стержня, в котором определяется нормальное напряжение, Н;
А - площадь поперечного сечения стержня, в котором определяется напряжение, м2.
Вектор нормального напряжения расположен перпендикулярно к плоскости поперечного сечения.
Знак нормального напряжения совпадает со знаком продольной силы в этом поперечном сечении.
Нормальные напряжения равномерно распределены по площади поперечного сечения и одинаковы по величине и знаку. Следовательно, все точки поперечного сечения равноопасны.
Данная формула справедлива для сечений, удаленных
от места приложения
сосредоточенных нагрузок на расстояние, превышающее
в 1,5-2 раза поперечные размеры сечения

3.3 Деформации. Закон Гука
абсолютная продольная деформация
абсолютная поперечная деформация
относительная продольная деформация
относительная поперечная деформация
Коэффициент Пуассона

Французский учёный, член Парижской АН (1812), почётный член Петербургской АН (1826). По окончании в 1800 г. Политехнической школы в Париже работал там же (с 1806 г. профессор). С 1809 г. – профессор Парижского университета.
Труды Пуассона относятся к теоретической и небесной механике, математике и математической физике. Он впервые записал уравнения аналитической механики в составляющих импульса.
Решил ряд задач теории упругости, ввёл коэффициент Пуассона и обобщил уравнения теории упругости на анизотропные тела.
В области небесной механики исследовал устойчивость движения планет Солнечной системы, занимался решением задач о возмущениях планетных орбит и о движении Земли вокруг её центра тяжести.
В теории потенциала ввёл уравнение Пуассона и применил его к решению задач по гравитации и электростатике.
Пуассону принадлежат работы по интегральному исчислению, исчислению конечных разностей, теории дифференциальных уравнений с частными производными, теории вероятностей, где он доказал частный случай больших чисел закона и одну из предельных теорем. Исследовал вопросы теплопроводности, магнетизма, капиллярности, распространения звуковых волн и баллистики. Был убеждённым сторонником атомизма П.С. Лапласа.
ПУАССОН (Poisson) Симеон Дени
(1781-1840)

В пределах упругих деформаций нормальное напряжение σ прямо пропорционально относительной продольной деформации.
где Е – модуль нормальной упругости (модуль упругости первого рода или модуль Юнга), Па.
- Закон Гука
За счет изменения формы и размеров любая конструкция сопротивляется (создает силы противодействия) внешним нагрузкам.
При достаточно больших внешних нагрузках (и, как следствие, больших внутренних напряжениях) межатомные связи материала могут быть разорваны, что приведет к разрушению конструкции.
Конструкция должна быть спроектирована так, чтобы она не разрушилась под нагрузкой. Деформации (перемещения), которые неизбежно возникают в конструкции под нагрузкой, должны быть вполне определенными и достаточно малыми, поскольку выбранные размеры и форма элементов конструкции обеспечивают определенное качество ее функционирования.
Так, изменение под нагрузкой размеров и формы элементов конструкции самолета, обтекаемых потоком воздуха, существенным образом влияет на аэродинамические характеристики и, как следствие, - на летно-технические характеристики самолета.

Английский естествоиспытатель, член Лондонского королевского общества (1663). В 1653г. поступил в Оксфордский университет, где впоследствии стал ассистентом Р.Бойля. С 1665г. – профессор Лондонского университета, в 1677–1683гг. – секретарь Лондонского Королевского общества.
В 1659 г. построил воздушный насос, совместно с Х. Гюйгенсом установил (около 1660) постоянные точки термометра – таяния льда и кипения воды.
Усовершенствовал барометр, зеркальный телескоп, применил зрительную трубу для измерения углов, сконструировал прибор для измерения силы ветра, машину для деления круга и другие приборы.
Большое значение имело открытие Гуком в 1660 закона пропорциональности между силой, приложенной к упругому телу, и его деформацией.
Гук высказал идею, что все небесные тела тяготеют друг к другу, и дал общую картину движения планет. Он предвосхитил закон всемирного тяготения И.Ньютона; в 1679 высказал мнение, что если сила притяжения обратно пропорциональна квадрату расстояния, то планета должна двигаться по эллипсу. Гук придерживался волновой теории света и оспаривал корпускулярную; теплоту считал результатом механического движения частиц вещества.
С помощью усовершенствованного им микроскопа Гук наблюдал структуру растений и дал чёткий рисунок, впервые показавший клеточное строение пробки (термин «клетка» был введён Гуком), а также описал строение клеток бузины, укропа, моркови и др.
Гук высказывал мысли об изменении земной поверхности, которое, по его мнению, повлекло изменение фауны. Гук считал, что окаменелости – это остатки прежде живших существ, по которым можно воспроизвести историю Земли.
Гук был известен также как архитектор. По его проектам было построено несколько зданий, главным образом в Лондоне.
ГУК (Хук) (Hooke) Роберт
(1635-1703)

Английский физик, врач и астроном, один из создателей волновой теории света. Член Лондонского королевского общества (1794), с 1802–1829гг. его секретарь. Обладая разносторонними способностями и интересами, Юнг уже в 8-летнем возрасте занимался геодезией и математикой, с 9 лет изучал языки (в том числе латинский, греческий, еврейский, арабский), историю, ботанику. Изучал медицину в Лондоне и Эдинбурге, учился в Гёттингенском университете, где слушал лекции Г.К.Лихтенберга. В 1801–1803гг. – профессор Королевского института в Лондоне. С 1811г. и до конца жизни работал врачом в больнице святого Георгия в Лондоне. Одновременно с 1818г. – секретарь Бюро долгот и редактор «Nautical Almanac».
Наиболее важные направления его работ – оптика, механика, физиология зрения, филология. В 1793г. в работе «Наблюдения над процессом зрения» указал, что аккомодация глаза обусловлена изменением кривизны хрусталика.
Оптические наблюдения привели Юнга к мысли, что господствовавшая в то время корпускулярная теория света неверна, и он высказался в пользу волновой теории. Его идеи вызвали возражения английских учёных, и под их влиянием Юнг отказался от своего мнения. Однако в 1800г. в трактате по оптике и акустике «Опыты и проблемы по звуку и свету» Юнг вновь пришёл к волновой теории света и впервые рассмотрел проблему суперпозиции волн; дальнейшим развитием этой проблемы явилось открытие им принципа интерференции (термин введён Юнгом в 1802).
В докладе «Теория света и цветов», прочитанном Юнгом Королевскому обществу в 1801г. (опубликован в 1802), он дал объяснение колец Ньютона на основе интерференции и описал первые опыты по определению длин волн света.
В 1803г. в работе «Опыты и исчисления, относящиеся к физической оптике» рассмотрел явления дифракции Он разработал также теорию цветного зрения, основанную на предположении о существовании в сетчатой оболочке глаза трёх родов чувствительных волокон, реагирующих на три основных цвета.
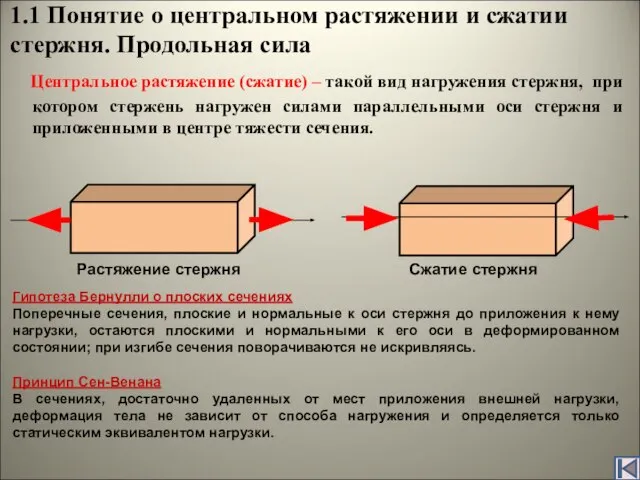
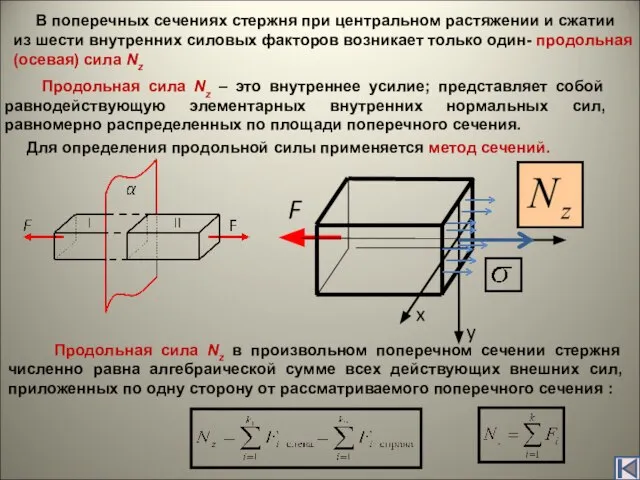
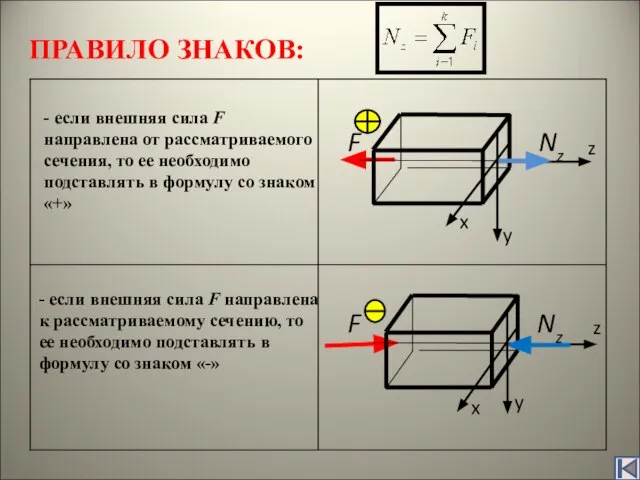
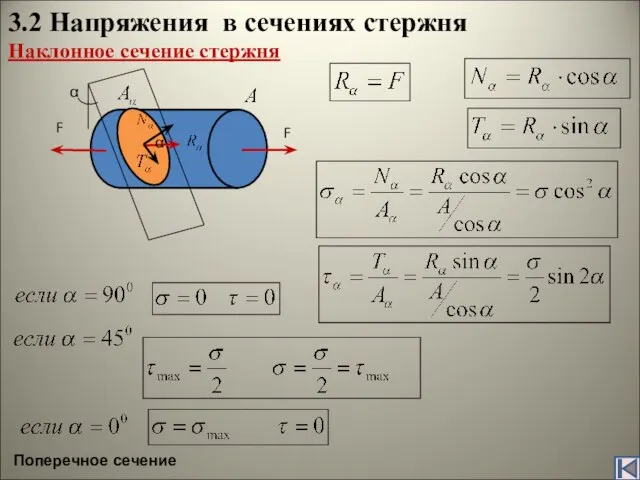
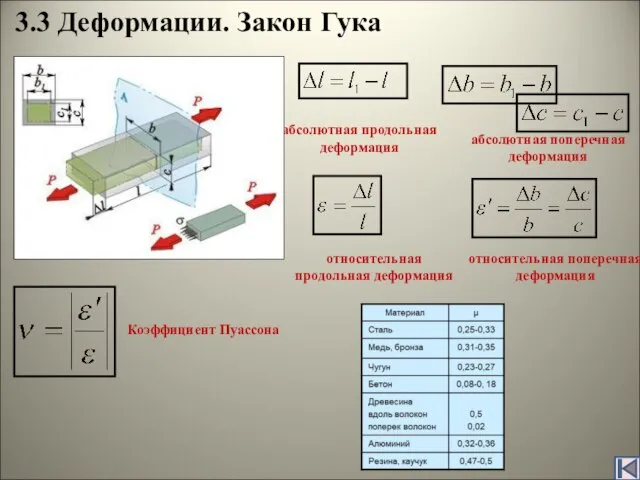
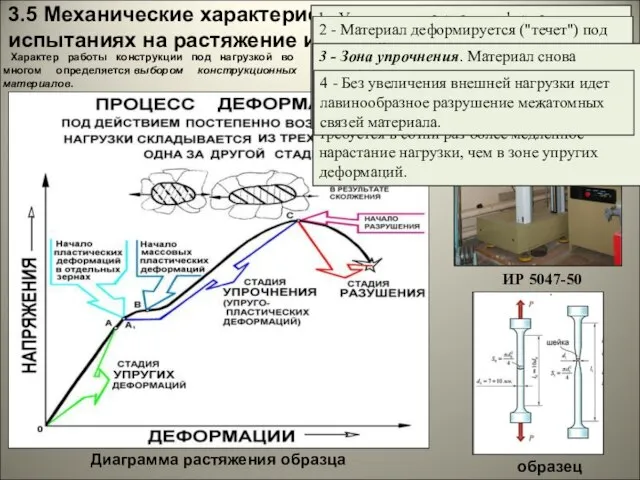
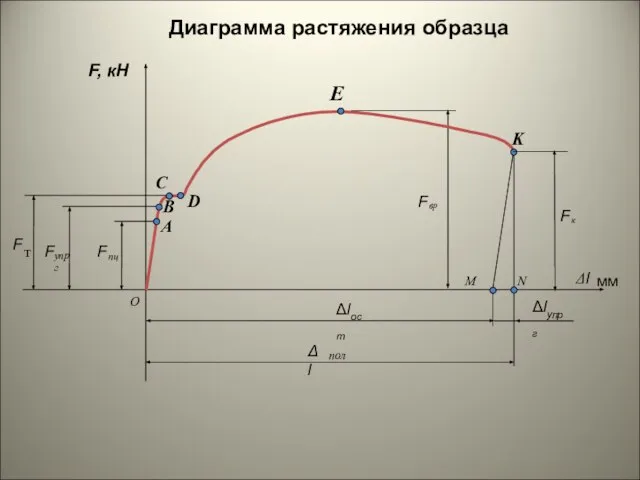
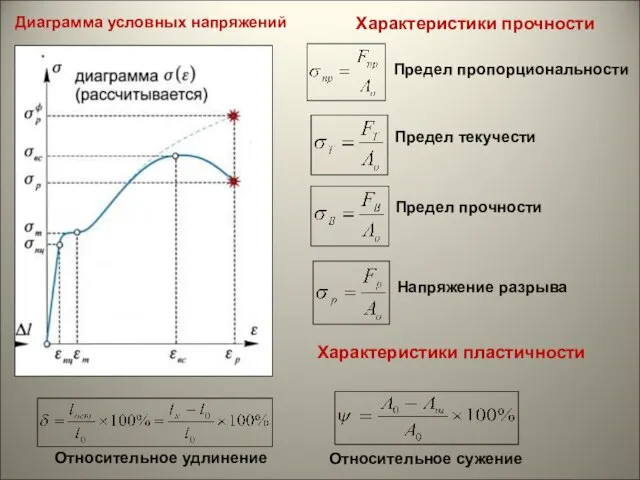
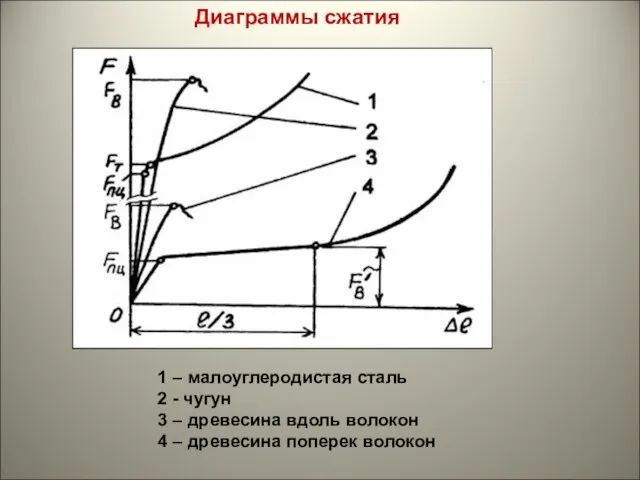
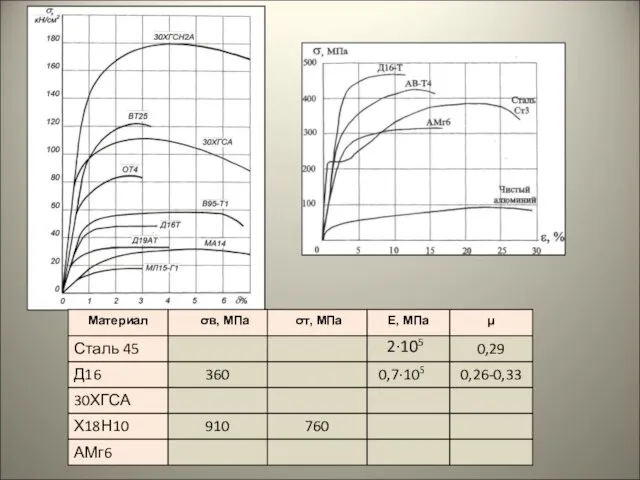
В 1807г. в 2-томном труде «Курс лекций по натуральной философии и механическому искусству» Юнг обобщил результаты своих теоретических и экспериментальных работ по физической оптике (термин ввёл Юнг) и изложил свои исследования по деформации сдвига, ввёл числовую характеристику упругости при растяжении и сжатии – так называемый модуль Юнга.
Он занимался расшифровкой египетских иероглифов (определил значение некоторых знаков Розеттского камня), был хорошим музыкантом, знатоком живописи.
ЮНГ (Янг) (Young) Томас
(1773-1829)

Деформация стержня при растяжении и сжатии выражается в изменении его длины и поперечных размеров.
Интенсивность деформации при растяжении или сжатии характеризуется относительным удлинением или укорочением.
Абсолютная деформация участка стержня
Абсолютная деформация стержня

3.5 Механические характеристики материалов при испытаниях на растяжение и сжатие
ИР 5047-50
образец
Диаграмма растяжения образца
1 - Увеличения нагрузки деформации пропорциональны напряжениям и при снятии нагрузки исчезают, т. е. образец за счет межатомных связей (сил упругости) возвращается в исходное (недеформированное) состояние.
2 - Материал деформируется ("течет") под нагрузкой и при снятии нагрузки не возвращается к исходному состоянию, в нем возникают остаточные пластические деформации за счет того, что часть межатомных связей разрушается.
3 - Зона упрочнения. Материал снова приобретает способность увеличивать сопротивление дальнейшей деформации, однако для удлинения образца в этой зоне требуется в сотни раз более медленное нарастание нагрузки, чем в зоне упругих деформаций.
4 - Без увеличения внешней нагрузки идет лавинообразное разрушение межатомных связей материала.
Характер работы конструкции под нагрузкой во многом определяется выбором конструкционных материалов.

Δl
мм
O
F, кН
А
В
С
D
E
K
Диаграмма растяжения образца

Характеристики прочности
Предел пропорциональности
Предел текучести
Предел прочности
Напряжение разрыва
Характеристики пластичности
Диаграмма условных напряжений
Относительное удлинение
Относительное сужение

Диаграммы сжатия
1 – малоуглеродистая сталь
2 - чугун
3 – древесина вдоль волокон
4 – древесина поперек волокон

0,7·105
2·105

3.4 Виды расчетов
Для обеспечения надежной работы и долговечности деталей машин, конструкций и сооружений проводятся различные расчеты. Наиболее распространенными являются расчеты на прочность и жесткость
Напряжение, при котором материал разрушается или в нем возникают заметные пластические деформации, называется предельным (разрушающим) напряжением σпред. Предельное напряжение выбирается в зависимости от материала и требований к конструкциям.
- для пластичных материалов предельным напряжением при растяжении (сжатии) является предел текучести;
- для хрупких материалов - предел прочности при растяжении σвр и предел прочности при сжатии σвс (при этом σвс > σвр)
Коэффициент запаса прочности
Из условия надежности работы деталей и конструкций величину максимального напряжения, возникающего в опасном (наиболее напряженном) сечении бруса, необходимо ограничивать некоторыми значениями.
Напряжение, при котором обеспечивается безопасная работа конструкции, называется допускаемым напряжением [σ].

Условие прочности выражается неравенством:
где σmax - наибольшее расчетное нормальное напряжение;
σadm- допускаемое нормальное напряжение
Расчет на прочность

проверочный расчет
(проверка расчетного напряжения в стержне)
Виды расчета на прочность:
проектный расчет
(подбор размеров поперечного сечения стержня)
- определение допускаемого значения продольной силы

Расчет на жесткость
Условие жесткости стержня выражается неравенством:
где Δl – абсолютная деформация стержня;
Δladm – допускаемая величина абсолютной деформации стержня.

Концентраторы напряжений - местные резкие изменения однородности (формы и, следовательно, жесткости) конструкции, приводящие к резкому местному (локальному) повышению напряжений в конструкции.
На рис. 10.7 показано действие растягивающей внешней нагрузки, равномерно распределенной по краям простейших конструктивных элементов - листов. Пунктирные линии представляют собой так называемые траектории напряжений, вдоль которых напряжение передается от молекулы к молекуле. Для гладкого листа эти линии параллельны, напряжения в любом сечении листа одинаковы.
.
Силы, передающиеся по траекториям напряжений в листах с концентраторами (надрез в кромке листа, отверстие в центре листа), обходят разрыв в материале. Плотность траекторий напряжений увеличивается, и локальные напряжения σ у края концентратора возрастают (иногда многократно). В этих местах может произойти нарушение (разрыв) межатомных связей, возникнут микротрещины, распространение которых ведет к разрушению конструкции.
Распределение напряжений в законцовках (местах соединения деталей) обычно особенно сложно, в них обязательно появляются концентрации напряжений - местное повышение напряжений.
В месте соединения (рис. 10.8) листов 1 и 3 с помощью заклепок (или сварных точек) 2 передача нагрузки будет происходить только через точки крепления. Листы равномерно включатся в работу на достаточно большом удалении от места соединения.
Заштрихованная область листов практически выключена из работы и не испытывает напряжений. В то же время напряжения в поперечных сечениях листов распределены неравномерно, причем σА-А > σБ-Б > σВ-В.
Конструктор особое внимание должен уделять выбору формы деталей, работающих на растяжение, и особенно их законцовок, чтобы уменьшить возможные концентрации напряжений

3.5 Проверочный тест
ВОПРОС
ОТВЕТ
Нормальные напряжения, действующие
в сечении 1-1
1- сжимающими
2- растягивающими и сжимающими
3- равны нулю
4- растягивающими
1- 0,4
2- 0,1
3- 0,25
4- 0,3
При испытаниях образцах на растяжение
Были определены продольная и поперечная
деформации. Они оказались равными
0,00032 и 0, 00013.
Тогда коэффициент Пуассона равен

ВОПРОС
ОТВЕТ
Если стержень ВС одинаково работает на растяжение
и сжатие, то проверку на жесткость проводят по условию
Проверку на жесткость стержня ВС проводят по условию

ВОПРОС
ОТВЕТ
Чугунный образец диаметром 0,015 м разрушился
при силе 0,12 Мн. Тогда величина предела
прочности равна
Проверку на прочность стержня АВ, имеющего разные
допускаемые напряжения на растяжение и сжатие,
проводят по формуле

ВОПРОС
ОТВЕТ
1- характеристику прочности,
равную 19%
2- относительную остаточную
деформацию, равную 2%
3- вязкую характеристику,
равную 30%
4- характеристику упругости,
равную 11%
По результатам испытания образца на
Растяжение вплоть до разрыва, можно
определить
Если стержень ВС одинаково работает на
растяжение и сжатие, то проверку прочности
проводят по формуле

ВОПРОС
ОТВЕТ
1- равны нулю
2- сжимающими
3- растягивающими и
сжимающими
4- растягивающими
Деформации, возникающие в сечении 1-1, будут
Проверку прочности стержня АВ, имеющего
разные допускаемые напряжения на растяжение
и сжатие, проводят по формуле