Содержание
- 2. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- 3. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ– физическое поле посредством которого осуществляется взаимодействие электрически заряженных частиц и частиц обладающих магнитным моментом.
- 4. МАГНИТНОЕ ПОЛЕ
- 5. МАГНИТНОЕ ПОЛЕ И ЕГО ХАРАКТЕРИСТИКИ
- 6. МАГНИТНОЕ ПОЛЕ МАГНИТНОЕ ПОЛЕ – одна из форм проявления элек-тромагнитного поля, отличающаяся только тем, что действует
- 7. Все постоянные магниты имеют два разноимен-ных полюса: северный и южный. Одноименные полюса взаимно отталкиваются, а разноименные
- 8. Магнитное поле не действует на неподвижные электри-ческие заряженные тела, но и эти частицы (тела) не действуют
- 9. МАГНИТНЫЙ МОМЕНТ МАГНИТНЫЙ МОМЕНТ – векторная величина, характеризующая магнитные свойства тел и частиц тела, для плоского
- 10. За положительное направление может быть принято направление, совпадающее с направлением силы, которая действует на северный полюс
- 11. МАГНИТНАЯ ИНДУКЦИЯ – ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ – силовая характе-ристика магнитного поля равная отношению силы, действующей со
- 12. МАГНИТНАЯ ИНДУКЦИЯ – в точке од- нородного магнитного поля опреде-ляется максимальным вращающим моментом, равным единице, когда
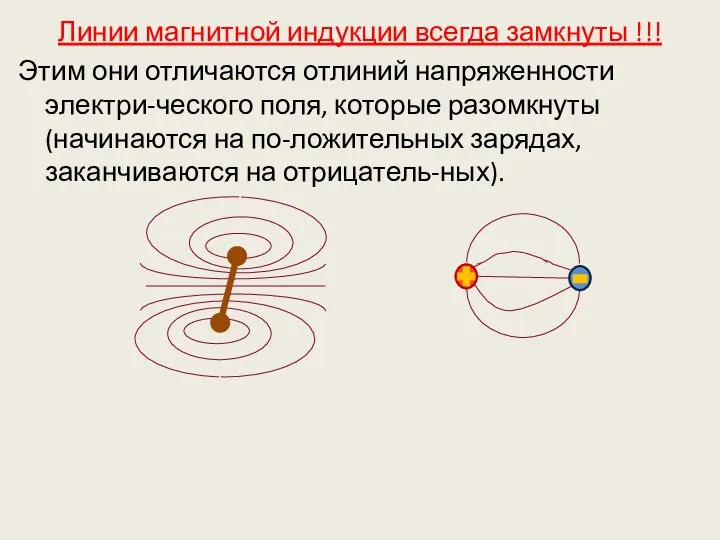
- 13. Линии магнитной индукции всегда замкнуты !!! Этим они отличаются отлиний напряженности электри-ческого поля, которые разомкнуты (начинаются
- 14. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ Ампер (1775-1836) предположил что в любом теле суще-ствуют микроскопические токи обусловленные движе-нием электронов
- 15. Магнитное поле макротоков описывается ВЕКТОРОМ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ . Для одно-родной изотропной среды вектор магнитной индукции
- 16. ЗАКОН БИО-САВАРА-ЛАПЛАСА
- 17. ЗАКОН БИО – САВАРА – ЛАПЛАСА Магнитное поле постоянного тока изучалось французами Био (1774-1862), Саваром (1791-1842)
- 18. Направление перпендикулярно и то есть перпенди-кулярно плоскости в которой они лежат, и совпадает с касательной к
- 19. МАГНИТНОЕ ПОЛЕ ПРЯМОГО ТОКА Магнитное поле тока текущего по прямому, тонкому, бесконечно длинному проводу. В произвольной
- 20. МАГНИТНОЕ ПОЛЕ В ЦЕНТРЕ КРУГОВОГО ПРОВОДНИКА С ТОКОМ Все элементы проводника в центре окруж-ности создают магнитное
- 21. ЗАКОН АМПЕРА. ВЗАИМОДЕЙСТВИЕ ПАРАЛЛЕЛЬНЫХ ТОКОВ
- 22. ЗАКОН АМПЕРА Магнитное поле ориентирует контур тока (рамку) в про-странстве, значит, вращающий момент, испытываемый рамкой, есть
- 23. Закон Ампера в скалярной форме Направление вектора может быть оп-ределено по правилу левой руки: В ладонь
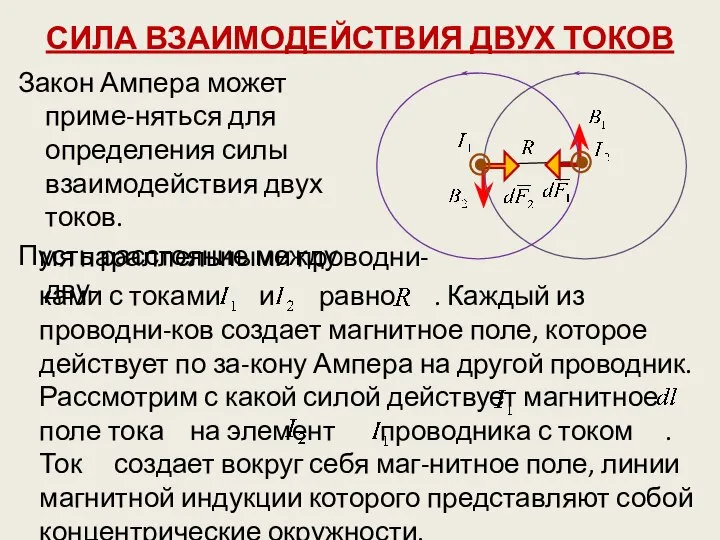
- 24. СИЛА ВЗАИМОДЕЙСТВИЯ ДВУХ ТОКОВ Закон Ампера может приме-няться для определения силы взаимодействия двух токов. Пусть расстояние
- 25. Направление задается правилом «правого винта», его абсолютное значение: Направление силы с которой поле действует на участок
- 26. МАГНИТНАЯ ПОСТОЯННАЯ. ЕДИНИЦЫ ИЗМЕРЕНИЯМАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ Если два параллельных проводника с токами находятся
- 27. вакууме на расстоянии 1 м один от другого, создаёт между проводниками силу равную 2*10⁻⁷ Н на
- 28. Единица измерения магнитной индукции – Тл (Тесла). 1 Тл – магнитная индукция такого однородного магнит-ного поля,
- 29. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЗАРЯДА
- 30. Каждый проводник с током создает в пространстве маг-нитное поле. Ток – упорядоченное движение электри-ческих зарядов. Значит
- 31. Формула магнитной индукции свободно двигающегося заряда в скалярной форме: Движущийся заряд по своим свойствам эквивалентен элементу
- 32. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ
- 33. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД Магнитное поле действует не только на проводники с то-ком, но
- 34. Абсолютное значение Силы Лоренца: α – угол между и . Магнитное поле действует только на движущиеся
- 35. Если на движущийся электрический заряд помимо маг-нитного поля действует и электрическое поле с нап-ряженностью , то
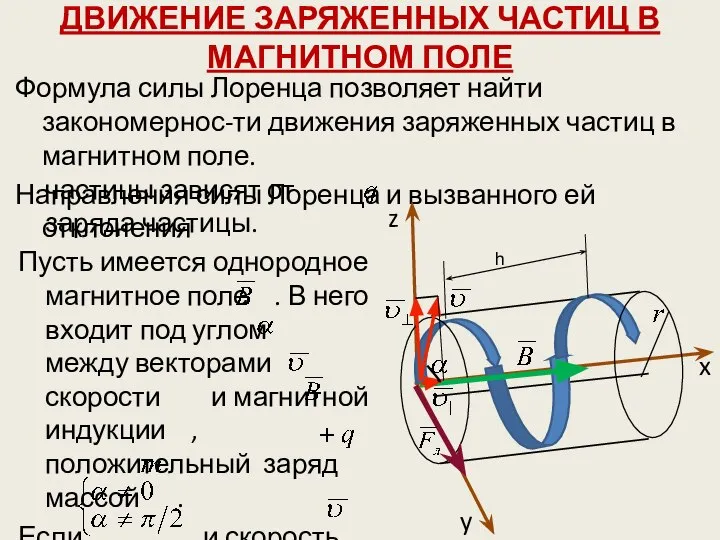
- 36. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ частицы зависят от заряда частицы. Пусть имеется однородное магнитное поле
- 37. частицы направлена под углом к , то её движение можно представить в виде суперпозиции: Равномерное прямолинейное
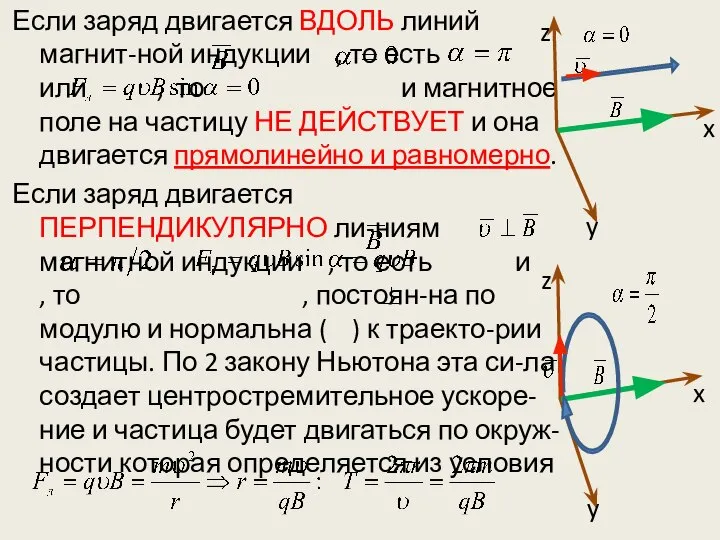
- 38. Если заряд двигается ВДОЛЬ линий магнит-ной индукции , то есть или , то и магнитное поле
- 39. ЭФФЕКТ ХОЛЛА Эффект Холла – возникновение в металле (или полупро-воднике) с током плотностью , помещенном в
- 40. распределение зарядов в поперечном направлении. - поперечная (холловская) разность потенциалов. - концентрация электронов - постоянная Холла(
- 41. ЦИРКУЛЯЦИЯ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ ДЛЯ МАГНИТНОГО ПОЛЯ В ВАКУУМЕ
- 42. Аналогично циркуляции вектора напряженности элек-тростатического поля в вакууме, Циркуляцией векто-ра по заданному замкнутому контуру называется интеграл
- 43. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОГО ПОЛЯ В ВАКУУМЕ (ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ) Циркуляция вектора
- 45. Скачать презентацию






































 Эпиграфы
Эпиграфы Концепции пространства - времени
Концепции пространства - времени Последовательное соединение
Последовательное соединение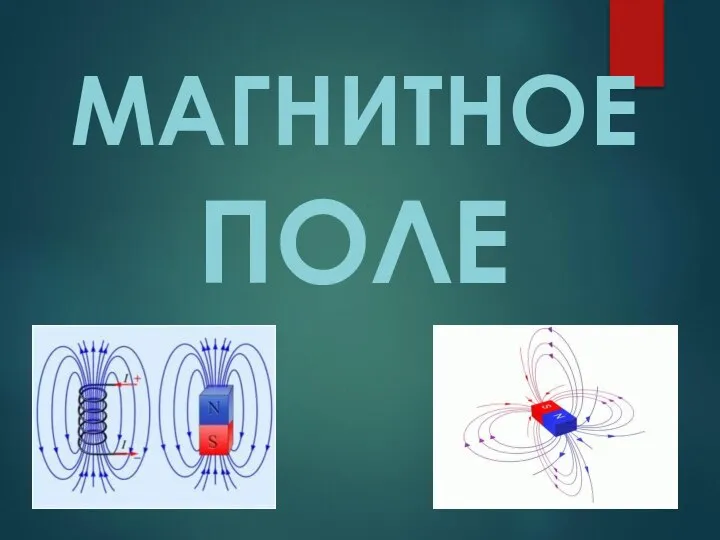 Магнитное поле
Магнитное поле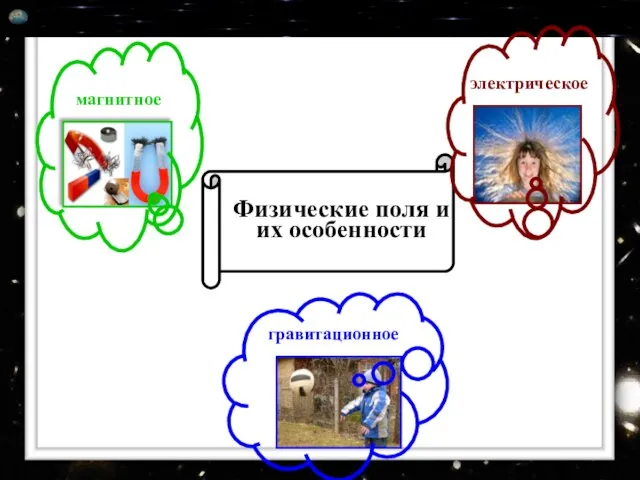 Презентация по физике "Физические поля и их особенности" -
Презентация по физике "Физические поля и их особенности" -  Поперечные и продольные волны. Энергия волны. Интерференция и дифракция волн. Звуковые волны
Поперечные и продольные волны. Энергия волны. Интерференция и дифракция волн. Звуковые волны Электричество. Простейшая электрическая цепь. Первая помощь при ударе электрическим током
Электричество. Простейшая электрическая цепь. Первая помощь при ударе электрическим током Закон Ома для участка цепи. Самостоятельная работа
Закон Ома для участка цепи. Самостоятельная работа Электрические явления
Электрические явления Презентация на тему Механическое движение
Презентация на тему Механическое движение  Кең ауқымды вибратор
Кең ауқымды вибратор Основные понятия фотометрии
Основные понятия фотометрии Презентация к ПЗ КП
Презентация к ПЗ КП Ядерные реакции. Атом, атомное ядро, атомная энергия (Лекция 2)
Ядерные реакции. Атом, атомное ядро, атомная энергия (Лекция 2) Коэффициент трения скольжения
Коэффициент трения скольжения Атом. Левкипп. V в. до н.э
Атом. Левкипп. V в. до н.э Сообщающиеся сосуды
Сообщающиеся сосуды Механическая работа. Единицы работы
Механическая работа. Единицы работы Сила Архимеда и условие плавания тел
Сила Архимеда и условие плавания тел Кинематика
Кинематика Геометрическая оптика. Линзы
Геометрическая оптика. Линзы Твердое тело в механике
Твердое тело в механике Трансформатор. Холостой и рабочий ход, Подача и потребление электроэнергии
Трансформатор. Холостой и рабочий ход, Подача и потребление электроэнергии Устройство швейной машины
Устройство швейной машины Лазер, устройство лазера
Лазер, устройство лазера Оптическая иллюзия
Оптическая иллюзия Определение температуры вспышки в закрытом тигле. Лабораторная работа
Определение температуры вспышки в закрытом тигле. Лабораторная работа Ньютон (урок физики в 10 классе)
Ньютон (урок физики в 10 классе)