Гидростатика

Основные понятия и теоретические положения
Примерами криволинейных поверхностей, испытывающих давление покоящейся жидкости, являются сферические и цилиндрические стенки резервуаров, секторные, сферические и цилиндрические затворы, клапаны насосов, поверхности трубопроводов и т. п.
В практике инженерных расчётов ставятся задачи определения силы давления на криволинейные поверхности, необходимые усилия для открытия клапанов и затворов или удержания их в закрытом положении.
Сложность определения силы давления на криволинейные поверхности заключается в том, что каждое элементарное усилие, действующее на криволинейную поверхность, направлено по нормали к элементарной площадке и имеет угол наклона по отношению к другому элементарному усилию.
Это значит, что при определении силы давления жидкости придётся интегрировать зависимость элементарной силы dF по площади криволинейной поверхности. Для инженерных расчётов это затруднительно.

Горизонтальная составляющая силы давления на криволинейную поверхность равна силе давления жидкости на плоскую вертикальную проекцию криволинейной поверхности:
Fх=(ρgyc)Sу
где ρ - плотность жидкости; Sу - площадь вертикальной проекции криволинейной поверхности; yс - координата центра тяжести вертикальной проекции, отсчитанная от свободной поверхности.

Рассмотрим сосуд с жидкостью, имеющий цилиндрическую по­верхность АВ с образующей, перпендикулярной плоскости чертежа и определим силу давления жидкости на эту поверхность.
Выделим объем жидкости АВСД, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями СВ и АД и свобод­ной поверхностью жидкости.
Покажем действующие силы на выделенный объем жидкости и рассмотрим условия равновесия выделенного объема жидкости в вер­тикальном и горизонтальном направлениях.
Схема определения сил давления на стенку
Запишем условие равновесия объема жидкости (АВСД) в верти­кальном направлении:
po SГ+G-FB=0
где Sг - площадь горизонтальной проекции поверхности АВ; G = pgV - сила тяжести выделенного объема жидкости, здесь V - объем жидкости; FВ - вертикальная составляющая силы давления. Из данного уравнения следует, что
FB= po SГ +G

Вертикальная составляющая силы давления жидкости на криво­линейную стенку равна силе тяжести жидкости в объеме V, называе­мом телом давления, и силе давления, действующей на свободную поверхность жидкости.
Тело давления - это объем, ограниченный рассматриваемой кри­волинейной стенкой, смоченной жидкостью, вертикальной цилиндрической поверхностью, проведенной через контур этой стенки и гори­зонтальной плоскостью, проведенной по свободной поверхности жидкости.

Условие равновесия того же объема жидкости в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ДЕ и СВ взаимно уравновешиваются и остается лишь сила давления на поверхность АЕ, т.е.
FАЕ - FГ = 0,

Силы FB определяются по формуле
FB= po SГ +G,
и FГ – по формуле
FГ = poSВ + ρghГSВ ,
но на­правлены будут противоположно. Под G понимается сила тяжести жидкости в объеме, равном АВСД, хотя и не заполненном жидко­стью.

Пример 1. Определить давление в характерных точках и сум­марную силу давления как распределенную нагрузку на стенку под­водного транспортного туннеля радиусом r=5 м и глубиной погружения Н=20 м.
Решение. 1. Определим избыточное давление в характерных точках А, В и С по уравнению F=ρgh, ограничиваясь левой половиной туннеля, так как распределение давления по правой части будет аналогичным; тогда
pA=ρghA= ρg(H-2r)=10000(20-2∙5)=0,1 МПа;
pВ=ρghВ= ρg(H-r)=0,15 МПа;
pС=ρghС= ρgH=0,2 МПа;
2. Как известно, горизонтальная составляю­щая Fг не зависит от формы смоченной криво­линейной поверхности и определяется как силовое воздействие жидкости на ее вертикальную проек­цию:
FГ = ρghСГSВ=ρghВ2r=10000 ∙ 15 ∙ 10=1.5 МН

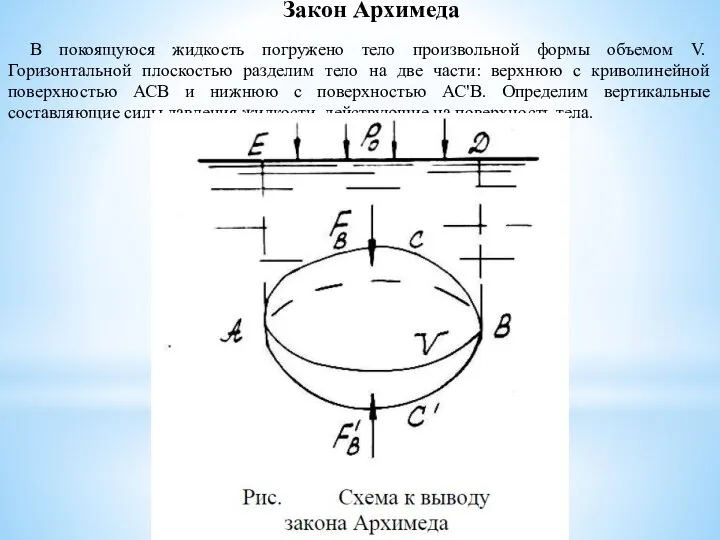
Закон Архимеда
В покоящуюся жидкость погружено тело произвольной формы объемом V. Горизонтальной плоскостью разделим тело на две части: верхнюю с криволинейной поверхностью АСВ и нижнюю с поверхностью АС'В. Определим вертикальные составляющие силы давления жидкости, действующие на поверхность тела.

ОТНОСИТЕЛЬНЫЙ ПОКОЙ ЖИДКОСТИ
Сведения из теории
Под относительным покоем понимается такое состояние, при котором в движущейся жидкости отдельные частицы не смещаются одна относительно другой. При этом жидкость перемещается как твердое тело. Само движение жидкости в этом случае можно назвать переносным движением. Для этого состояния характерно постоянство формы объема жидкости. Очевидно, что рассматриваемая масса жидкости будет неподвижна в координатной системе, связанной с движущимся резервуаром.
На жидкость, находящуюся в относительном покое, действуют массовые силы (силы тяжести и силы инерции переносного движения), а из поверхностных – силы давления.
Рассмотрим два частных случая относительного покоя: покой при переносном прямолинейном движении и покой при переносном вращательном движении вокруг вертикальной оси.

Относительный покой при прямолинейном движении на наклонной плоскости
Рассмотрим движение резервуара с жидкостью с постоянным ускорением a по наклонной плоскости, образующей угол α с горизонтальной плоскостью
Жидкость в движущемся резервуаре находится под действием силы давления, силы тяжести и силы инерции переносного движения. Ускорение силы инерции j=a и направлено в сторону, обратную ускорению резервуара a. Результирующий вектор массивных сил определяется диагональю параллелограмма, построенного на ускорениях сил тяжести g и инерции j.
Поступательное движение по
наклонной плоскости

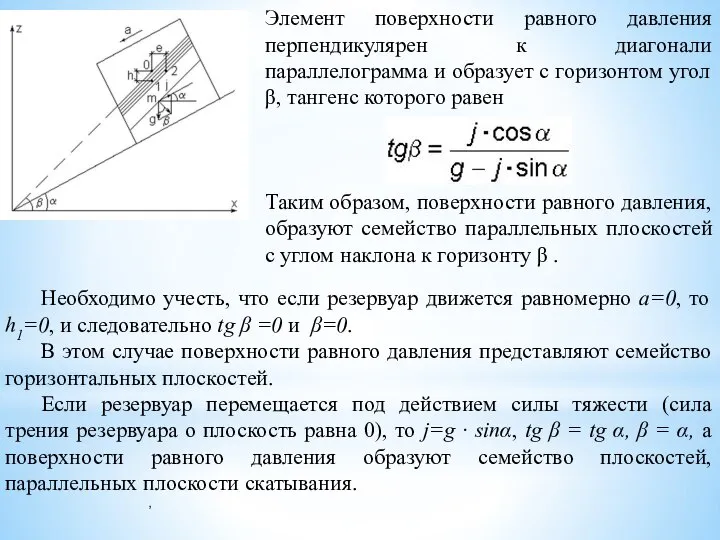
Элемент поверхности равного давления перпендикулярен к диагонали параллелограмма и образует с горизонтом угол β, тангенс которого равен
Таким образом, поверхности равного давления, образуют семейство параллельных плоскостей с углом наклона к горизонту β .
,
Необходимо учесть, что если резервуар движется равномерно a=0, то h1=0, и следовательно tg β =0 и β=0.
В этом случае поверхности равного давления представляют семейство горизонтальных плоскостей.
Если резервуар перемещается под действием силы тяжести (сила трения резервуара о плоскость равна 0), то j=g ∙ sinα, tg β = tg α, β = α, а поверхности равного давления образуют семейство плоскостей, параллельных плоскости скатывания.

Если резервуар перемещается с ускорением, но вертикально(a=900), то tg β =0 и β=0, а поверхности равного давления образуют семейство горизонтальных плоскостей.
Найдем закон распределения давления в вертикальной плоскости x=const.
Учитывая, что система координат перемещается вместе с резервуаром, Y=0, а для выбранной плоскости и dx=0, уравнение
примет вид:
В этом случае z=j ∙ sin a – g.
Тогда dp=ρ(j ∙ sin a – g)dz;

После интегрирования имеем:
Для двух точек 0 и 1 с координатами z0 и z1 имеем:
или
Если α=0, то имеем
а свободная поверхность имеет угол наклона к горизонту
При свободном падении резервуара
α=g, j=g и p1=p2=p0 , то есть во всем
объеме давление одинаково.

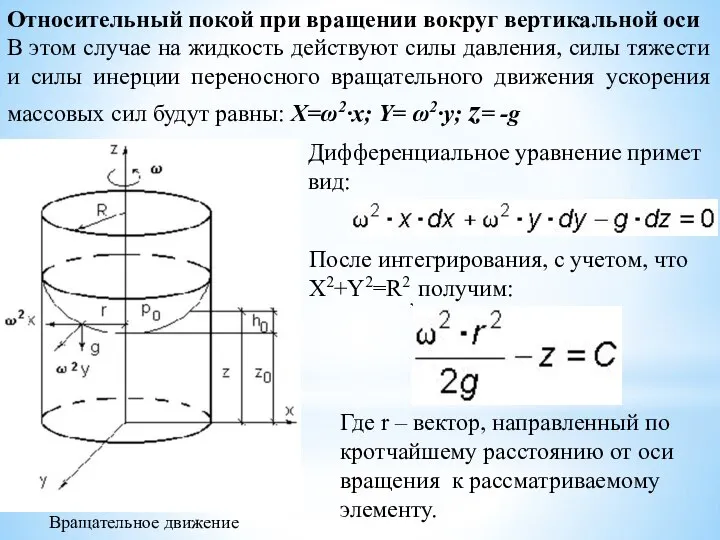
Относительный покой при вращении вокруг вертикальной оси
В этом случае на жидкость действуют силы давления, силы тяжести и силы инерции переносного вращательного движения ускорения массовых сил будут равны: Х=ω2∙х; Y= ω2∙y; z= -g
Вращательное движение
Дифференциальное уравнение примет вид:
После интегрирования, с учетом, что
X2+Y2=R2, получим:
Где r – вектор, направленный по
кротчайшему расстоянию от оси
вращения к рассматриваемому
элементу.

Это уравнение является уравнением параболоида вращения, а поверхности равного давления образуют семейство параболоидов вращения, сдвинутых вдоль вертикальной оси. Каждый параболоид характеризуется некоторым значением постоянной С. Для параболоида свободной поверхности принимаем, что при z= z 0, Х=Y=0 поэтому C = - z 0.
Тогда уравнение свободной поверхности примет вид:
или

Закон распределения давления по объему жидкости получим из уравнения
подставив в него соответствующие значения X, Y и Z. После интегрирования получаем:
Постоянную интегрирования C определим из условия, что при z= z 0 и r=0, p=p0, т.е. С=p0+ρ ∙ g ∙ z 0
После подстановки окончательно имеем:
Для частиц жидкости расположенных на одной вертикали можем записать:
где
т.е. существует обычный гидростатический закон распределения давления. Это объясняется тем, то проекции сил инерции на ось 0 равна нулю.

Пример 2. Сосуд с прямоугольным основанием L∙B наполнен водой до высоты h и движется по горизонтальной поверхности с ускорением a. Определить избыточное давление воды на дно сосуда у передней и задней стенок в точках 1 и 2.
Решение: При горизонтальном движении сосуда с ускорением a свободная поверхность жидкости станет наклонной к горизонту под углом β. Так как a= - j, то tgβ= - a/g. Учитывая что объем воды не изменяется, поэтому свободная поверхность повернется вокруг оси О, расположенной на середине длины сосуда, а повышение и понижение свободной поверхности у торцовых стенок будет одинаковым и равным ∆h .
Избыточное давление в точке 1 будет равно:
В точке 2 избыточное давление составит:

Пример 3. Цилиндрический сосуд радиусом R1 наполнен жидкостью плотностью ρ до уровня a в открытой трубке малого диаметра, установленной на крышке сосуда на расстоянии R2 от центра, и приведен в равномерное вращение относительно центральной вертикальной оси. Определить угловую скорость вращения сосуда, при которой избыточное давление под крышкой в центре сосуда будет равно 0.
Решение: Используя уравнение
найдем закон распределения избыточного давления в жидкости, заполняющей сосуд, учитывая что p0=ратм