Графическое представление физического процесса - функция

В окружающем нас мире происходят различные
физические явления и процессы, которые можно
описать функциональными зависимостями
переменных, в том числе и линейными.

В физике понятие "функция" используется
для исследования и описания различных
зависимостей физических величин, в том числе
всех физических законов, для эмпирического
исследования физических процессов и явлений;
при решении задач графическим методом и т.д.
Графическое представление физического процесса
делает его более наглядным, наполняет абстрактные
математические закономерности конкретным
физическим содержанием.

Линейная функция используется
для описания прямолинейного
равномерного движения
координаты материальной точки x(t);
-перемещения s=vt;
-скорости v=v0;
-ускорения а=0.

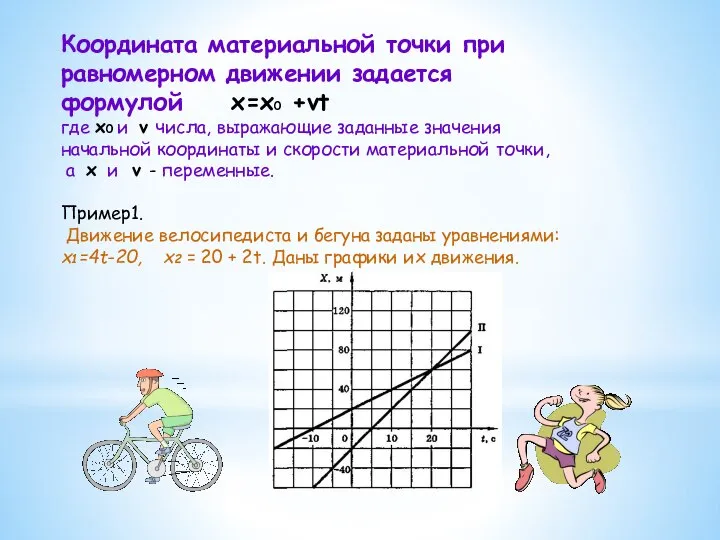
Координата материальной точки при равномерном движении задается
формулой x=x0 +vt
где x0 и v числа, выражающие заданные значения
начальной координаты и скорости материальной точки,
а x и v - переменные.
Пример1.
Движение велосипедиста и бегуна заданы уравнениями:
x1=4t-20, х2 = 20 + 2t. Даны графики их движения.

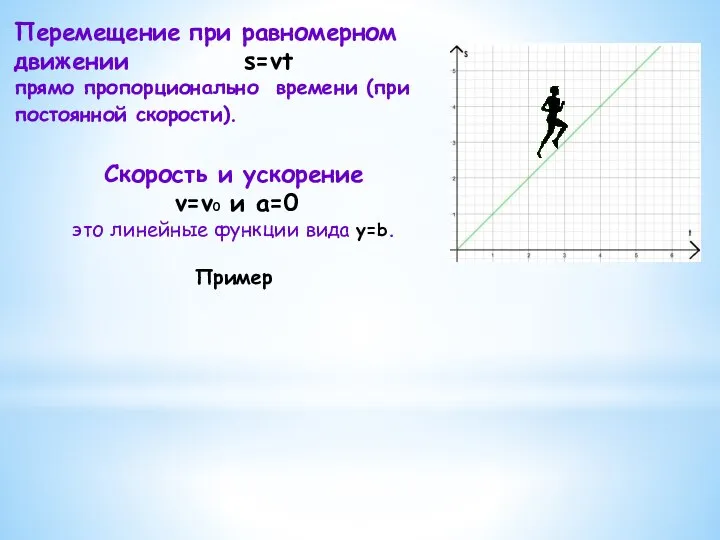
Перемещение при равномерном движении s=vt
прямо пропорционально времени (при постоянной скорости).
Скорость и ускорение
v=v0 и a=0
это линейные функции вида y=b.
Пример

В равноускоренном движении
линейная функция описывает
- скорость v(t);
- ускорение a(t).

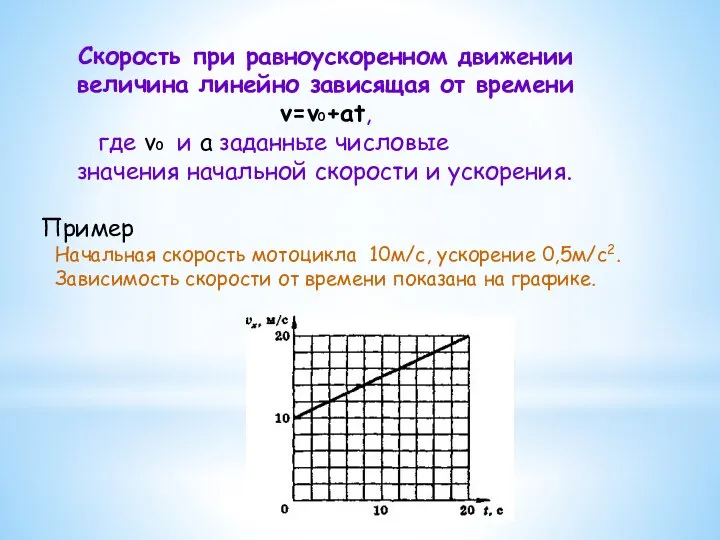
Скорость при равноускоренном движении
величина линейно зависящая от времени
v=v0+at,
где v0 и a заданные числовые
значения начальной скорости и ускорения.
Пример
Начальная скорость мотоцикла 10м/с, ускорение 0,5м/с2.
Зависимость скорости от времени показана на графике.

Ускорение при равноускоренном движении
величина постоянная и выражается уравнением
а=а0,
где а0 числовое значение ускорения,
т.е. линейная функция вида у=b
(график а=3м/с)

Линейная функция
широко используется при выводе
и описании физических законов:
закона Гука;
закона Ома;
2-ого закона Ньютона;
закона Архимеда;
закон всемирного тяготения;
закон Кулона;
и т.д.

.
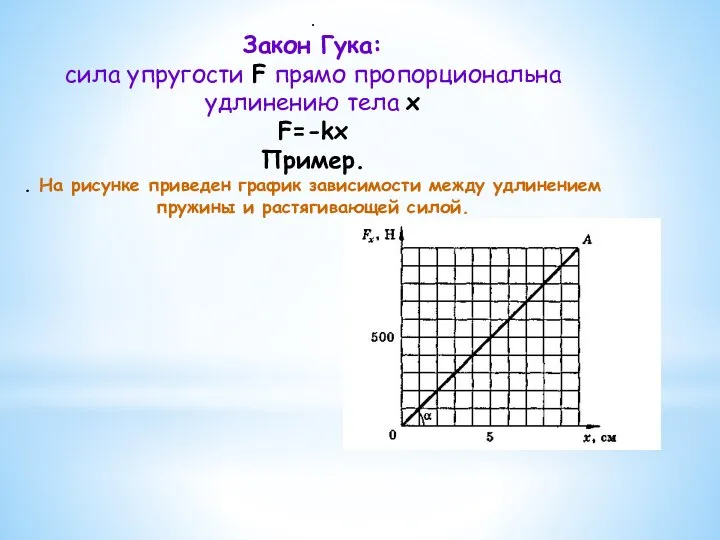
Закон Гука:
сила упругости F прямо пропорциональна
удлинению тела х
F=-kx
Пример.
. На рисунке приведен график зависимости между удлинением
пружины и растягивающей силой.

Закон Ома:
сила тока I прямо пропорциональна
напряжению U на концах проводника и обратно пропорционально сопротивлению R.
I=U/R
Зависимость силы тока I от напряжения U называется вольтамперной характеристикой I(U) металлического проводника
Пример
Найдите сопротивление (коэффициенты пропорциональности) двух проводников по вольтамперным характеристикам и сравните их.

По 2-ому закону Ньютона
ускорение полученное телом массой m пропорционально приложенной к нему силе F
F=ma (при фиксированном значении массы m)
Закон Всемирного тяготения,
также открытый Ньютоном, гласит:
Все тела во Вселенной притягиваются друг
к другу с силой, прямо пропорциональной
произведению их масс и обратно пропорци-
ональной квадрату расстояния между ними
F=G m1 m2
R2
Очевидно, что при фиксированном расстоянии R,
мы получаем только линейную зависимость F(m).

Закон Архимеда
FA=ρgVT,
где прослеживается прямо пропорциональная зависимость между FA силой Архимеда и VT объёмом тела погружённого в жидкость, при постоянных значениях g и ρ.

Линейная функция описывает различные физические процессы:
-изопроцессы в термодинамике;
-объёмное сжатие и растяжение;
-трение
и т.д.

Изопроцессы
Рассмотрим например изохорический процесс т.е. процесс при постоянном объеме. При повышении температуры t будет повышатьсяи давление p,прямо пропорционально температуре
Пример На рисунке представлены две изохоры для газа одной и той же массы.

Объёмное сжатие и растяжение
На рисунке дан график зависимости упругого напряжения,
возникающего в бетонной свае, от ее относительного сжатия.
Можно найти модуль упругости бетона.

Сила трения
F= μN
т.е. значение силы трения F прямо пропорционально силе реакции опоры N, где μ коэффициент трения.