Квантовый протокол E91. Неравенства Белла

Криптография - наука об изобретении кодов и шрифтов, известная со времен Цезаря. Ее популярность обусловлена особой важностью секретной передачи информации.
Квантовая криптография — метод защиты коммуникаций, основанный на явлениях квантовой физики. Ее отличием стало использование не математических методов, а – физических.
Одним из перспективных направлений в квантовой криптографии является использование перепутанных состояний для создания секретного ключа. Соответствующий протокол был предложен Экертом в 1991 году, и в литературе его обозначают E91.
Введение

и соответствующие волновые вектора удовлетворяют условию фазового синхронизма
- это совместное состояние не менее двух квантовых систем, которое получается, если системы происходят из одного источника либо взаимодействовали в прошлом.
Перепутанное состояние

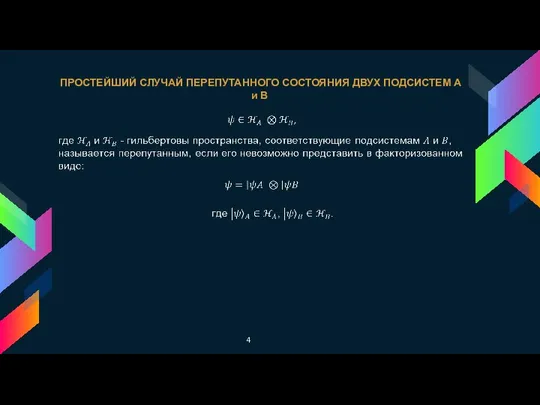
ПРОСТЕЙШИЙ СЛУЧАЙ ПЕРЕПУТАННОГО СОСТОЯНИЯ ДВУХ ПОДСИСТЕМ А и В

ВОЗМОЖНОЕ ИЛЛЮСТРАТИВНОЕ ПРЕДСТАВЛЕНИЕ
ЧИСТЫХ И СМЕШАННЫХ ПЕРЕПУТАННЫХ СОСТОЯНИЙ

Следуя Д. Бому, перепутанное состояние двух частиц с полуцелым спином (кубитов), которые образуются в результате распада частицы со спином 0. Суммарный спин двух частиц при этом сохраняется и равен 0, поэтому спины кубитов должны быть строго антикоррелированы. Вектор состояния данного синглетного состояния двух кубитов имеет вид

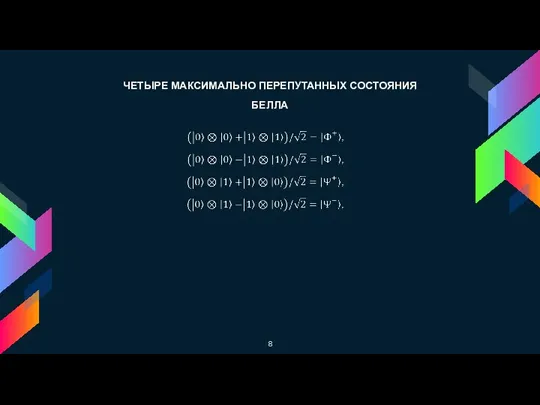
ЧЕТЫРЕ МАКСИМАЛЬНО ПЕРЕПУТАННЫХ СОСТОЯНИЯ БЕЛЛА

Из этого следует, что при измерении вдоль одной и той же оси квантово-механическое среднее в синглетном состоянии равно −1, являясь математическим выражением антикорреляции. Как было впервые показано Д. Беллом, квантовомеханическое среднее противоречит результату, выводимому из теории “скрытых параметров”.

где N, M = ±1 описывают зависящие от скрытого параметра λ статистики локальных измерений Алисы и Боба соответственно

Квантовая механика предсказывает следующее значение коррелятора в синглетном состоянии:
Для вычисления этого же коррелятора в рамках теории скрытых параметров напомним, что в силу принятия значений +1 или −1 наблюдаемыми a, b, c, d, то есть их дихотомичности, имеем
СПЕЦИАЛЬНЫЙ СЛУЧАЙ НЕРАВЕНСТВ БЕЛЛА И КХШХ (CHSH)

СХЕМА ПРОТОКОЛА ЭКЕРТА