Содержание
- 2. Мы знаем, что : на микроскопическом уровне все вещество - твердые тела, жидкости, газы, любые биологические
- 3. О каких конкретно явлениях и процессах идет речь? Тепловые явления и макроскопические параметры вещества - нагревание
- 4. Повторение: Что мы знаем про атомы и молекулы? (параметры и характеристики) Термодинамика и статистическая физика
- 5. Молекула - наименьшая частица вещества, определяющая его свойства и способная к самостоятельному существованию. Молекулы построены из
- 6. Типичный размер атомов: d ~ 10-10 м ; молекул ~>10-10-7 м Единица измерения атомных расстояний: 1
- 7. Атомная единица массы (1 а.е.м. = 1 Дальтон (Да)) приблизительно равна массе самого легкого в природе
- 8. Количество вещества - это число составляющих его атомов и/или молекул. Для любых макроскопически заметных количеств это
- 9. Вещество, с которым мы имеем дело при обычных земных условиях, может находиться в двух принципиально разных
- 10. Потенциальная энергия взаимодействия молекул Существование двух существенно разно-плотных состояний вещества - газообразного и конденсированного – качественно
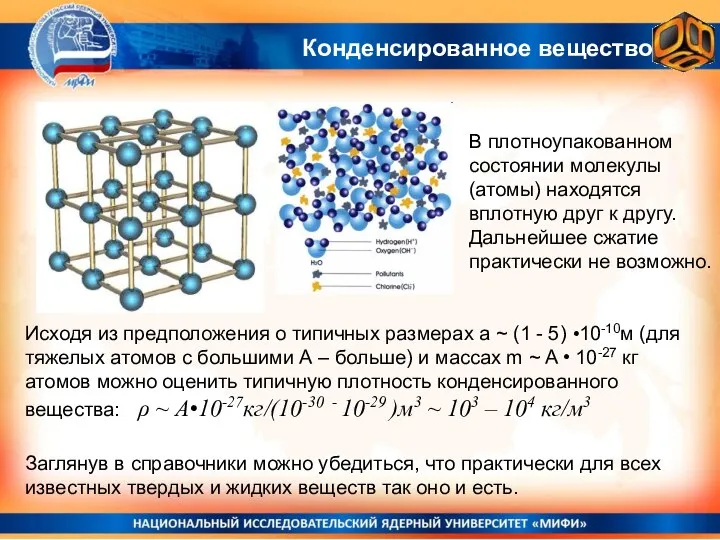
- 11. Конденсированное вещество В плотноупакованном состоянии молекулы (атомы) находятся вплотную друг к другу. Дальнейшее сжатие практически не
- 12. Известен экспериментальный факт (закон Авогадро): при нормальных условиях (давление равно давлению в земной атмосферы на уровне
- 13. Идеальный газ – самая простая модель самого простого состояния вещества. Лектор: доцент НИЯУ МИФИ, Андрей Станиславович
- 14. Газ: расстояние между молекулами много больше размера молекул (d>>r ~ в 10 раз в нормальных условиях
- 15. Идеальный газ Вещество находится в газообразном состоянии если суммарная кинетическая энергия молекул много больше абсолютного значения
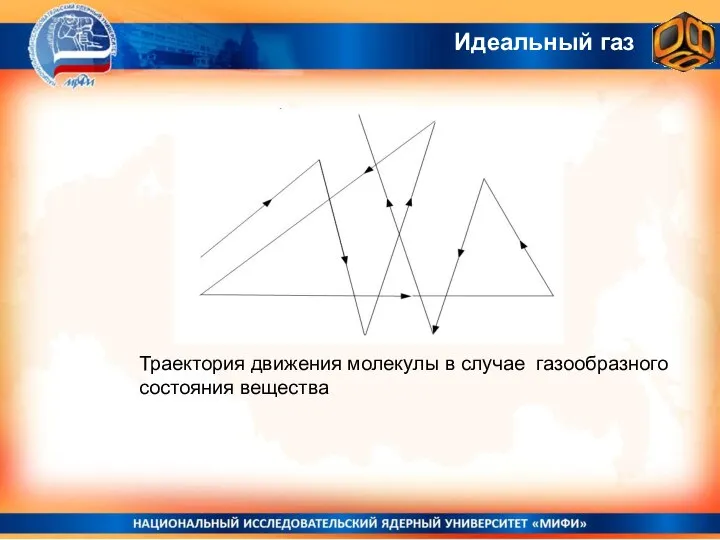
- 16. Траектория движения молекулы в случае газообразного состояния вещества Идеальный газ
- 17. Для практического описания состояний разреженных газов, близких к идеальному, используется всего несколько усредненных макро-параметров: V [м3]
- 18. Среднее значение квадрата скорости молекул Бессмысленно пытаться проследить за движением всех молекул - их слишком много.
- 19. Давление идеального газа После упругого удара о стенку молекулы массы m, она отлетает , сменив знак
- 20. Температура. Основное уравнение МКТ для идеального газа: Р = 2/3n = nΘ = nkT Θ =
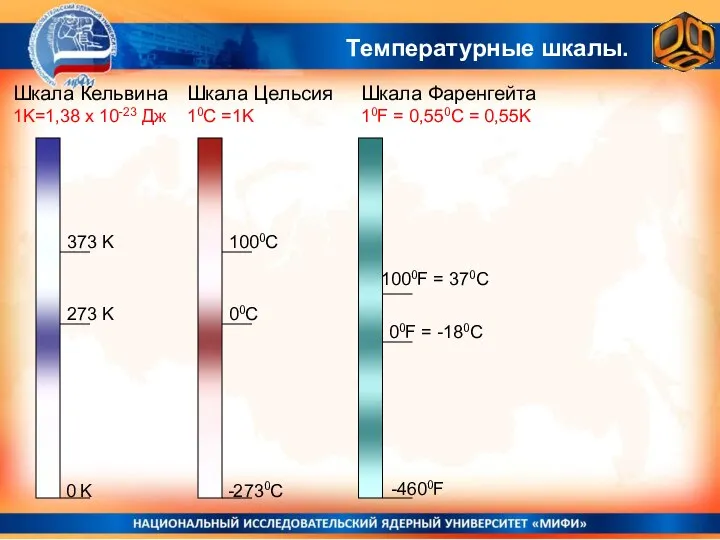
- 21. Температурные шкалы. Шкала Кельвина 1K=1,38 х 10-23 Дж 0 K 273 K 373 K -2730С 00С
- 22. Макроскопическое уравнение идеального газа Основное уравнение: Р = nkT Выразим n (число молекул в единице объема)
- 23. Газовые законы РV = (M/μ)RT = νRT Уравнение состояния идеального газа (Д.И.Менделеев(1874) – Б.Клапейрон (1834)) PV
- 25. Скачать презентацию



















 Приборы для измерения температуры
Приборы для измерения температуры Презентация на тему Экономия использования энергетических ресурсов на земле
Презентация на тему Экономия использования энергетических ресурсов на земле  Почему радуга разноцветная?
Почему радуга разноцветная? Контрольная работа
Контрольная работа Трехфазные цепи
Трехфазные цепи Законы геометрической оптики
Законы геометрической оптики Відновлення працездатності засобами фізичної рекреації
Відновлення працездатності засобами фізичної рекреації Дисперсные системы
Дисперсные системы Теория автоматического управления. Типовые звенья
Теория автоматического управления. Типовые звенья ГК_Практичекое занятие (5)
ГК_Практичекое занятие (5) Механическое движение. Траектория, путь, перемещение. Относительность движения
Механическое движение. Траектория, путь, перемещение. Относительность движения Механика. Повторение. Занятие 7
Механика. Повторение. Занятие 7 Математическая модель линейной динамической системы в форме проблемных матриц. Лекция #3
Математическая модель линейной динамической системы в форме проблемных матриц. Лекция #3 Устройство для наматывания нижней нити на шпульку
Устройство для наматывания нижней нити на шпульку Техническая механика. Срез, смятие, расчетные формулы
Техническая механика. Срез, смятие, расчетные формулы Конвекция. Примеры конвекции
Конвекция. Примеры конвекции Ременная передача
Ременная передача Электромагнитные колебания
Электромагнитные колебания Физические явления
Физические явления Ремонт портальных мостов. Учебное пособие
Ремонт портальных мостов. Учебное пособие Управление параметрами излучения мультиферроиковой структуры электрическим полем
Управление параметрами излучения мультиферроиковой структуры электрическим полем Потери давления при движении потоков двухфазных
Потери давления при движении потоков двухфазных Теоретическая механика. Часть 1. Кинематика. Глава 3. Движение твердой среды
Теоретическая механика. Часть 1. Кинематика. Глава 3. Движение твердой среды Электрическая цепь. Электротехнические материалы и изделия
Электрическая цепь. Электротехнические материалы и изделия Влажность. Решение задач. 8 класс
Влажность. Решение задач. 8 класс Теория относительности. (Лекция 4)
Теория относительности. (Лекция 4)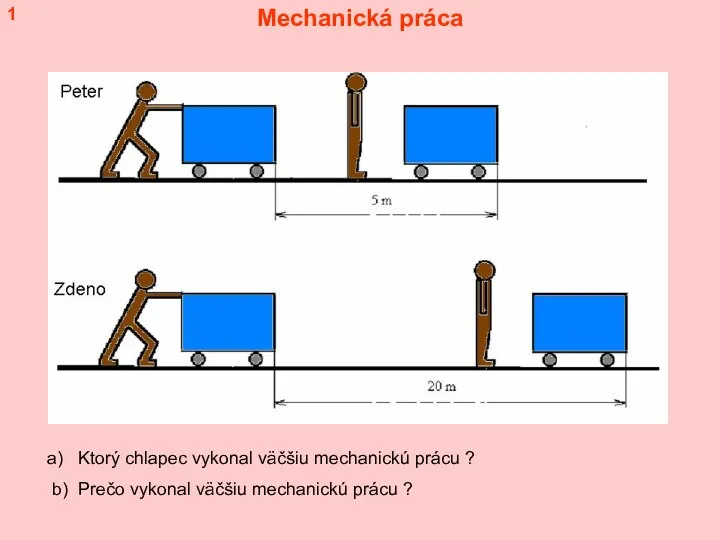 Mechanická práca
Mechanická práca Презентация на тему Идеальный газ в МКТ
Презентация на тему Идеальный газ в МКТ