Содержание
- 2. У гомогенному випадку фазовий перехід - це перехід від однофазного стану, в якому взагалі не існує
- 3. Слід пам'ятати, що паралельно з процесом фазового переходу - плавлення-кристалізації йде незалежний процес затвердіння-розрідження, який не
- 4. Повторення основ фізичної хімії
- 5. Рівноважна температура переходу при постійному тиску з твердого в рідкий стан T∞ в рівноважній термодинамічній системі
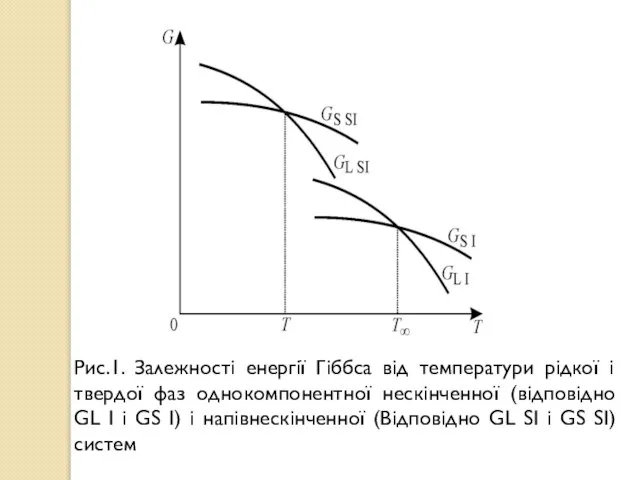
- 6. Рис.1. Залежності енергії Гіббса від температури рідкої і твердої фаз однокомпонентної нескінченної (відповідно GL I і
- 7. (4) Поява додаткових доданків в рівності (4) у порівнянні з (2) приводить до збільшення значення потенціалу
- 8. (7) Приймається допущення, що теплота плавлення також не залежить від температури, при якій відбувається фазовий перехід.
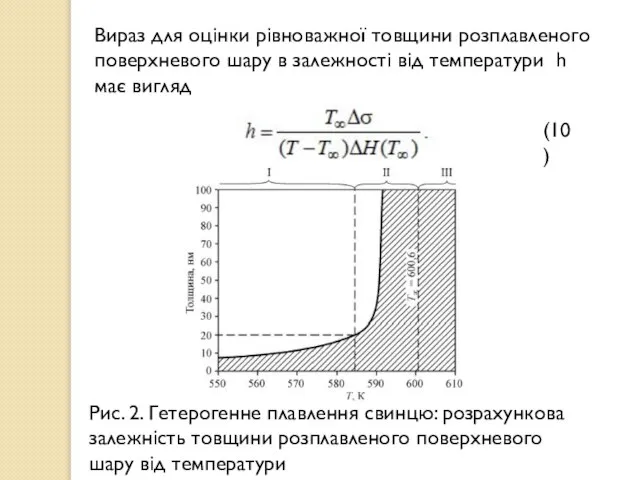
- 9. Вираз для оцінки рівноважної товщини розплавленого поверхневого шару в залежності від температури h має вигляд (10)
- 10. Висновки 1) наявність поверхні в напівнескінченній системі, і, як наслідок, виникнення явища плавлення, викликаного цією поверхнею,
- 11. 2. Залежність температури плавлення нанорозмірних систем від їх розмірів Для систем розмірами (діаметром нанокристалів, товщиною тонкої
- 12. Нанорозмірні системи можна умовно розділити на дві групи: 1) Системи, в яких немає можливості для зміни
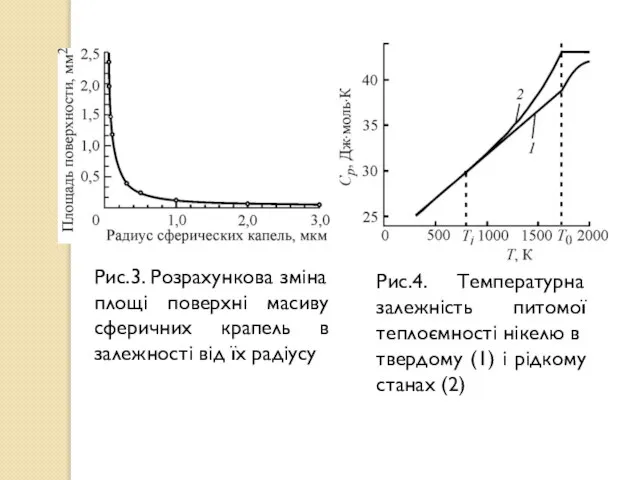
- 13. Рис.3. Розрахункова зміна площі поверхні масиву сферичних крапель в залежності від їх радіусу Рис.4. Температурна залежність
- 14. 3. Залежність температури плавлення нанорозмірних систем від їх розмірів без зміни форми 3.1. Нанокристали, нанокластери у
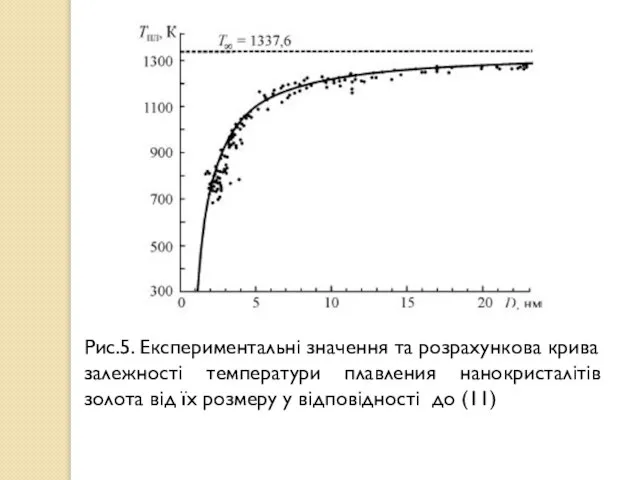
- 15. Рис.5. Експериментальні значення та розрахункова крива залежності температури плавления нанокристалітів золота від їх розмеру у відповідності
- 16. 3.2 Нитьовидні нанокристали, оточені іншим твердим розчином Рис. 6. Нитьовидні нанокристали індію у матриці пористого анодного
- 18. Скачать презентацию











 Электричество и магнетизм. Лекция 09
Электричество и магнетизм. Лекция 09 Подсистема управления маршрутами общественного транспорта
Подсистема управления маршрутами общественного транспорта Подготовка к итоговой проверочной работе по физике (6 класс)
Подготовка к итоговой проверочной работе по физике (6 класс) Сельскохозяйственные машины
Сельскохозяйственные машины Преобразования сигналов и Вейвлет-преобразование
Преобразования сигналов и Вейвлет-преобразование Механическая работа
Механическая работа Теплотехника как наука
Теплотехника как наука Использование наноматериалов в технике
Использование наноматериалов в технике Физические приборы вокруг нас
Физические приборы вокруг нас Вещество в электрическом поле
Вещество в электрическом поле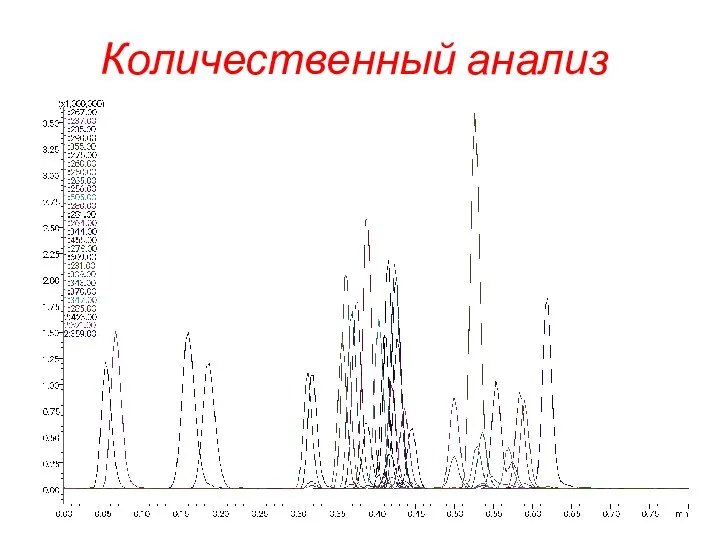 Количественный анализ
Количественный анализ Геометрическая оптика. Линзы
Геометрическая оптика. Линзы Агрегатные состояния вещества. Различие в молекулярном строении твердых тел, жидкостей и газов (7 класс)
Агрегатные состояния вещества. Различие в молекулярном строении твердых тел, жидкостей и газов (7 класс) Тяговая лебедка УК25-9-18
Тяговая лебедка УК25-9-18 Давление газа. 7 класс
Давление газа. 7 класс Снежные причуды. Всё о снеге и снежинках
Снежные причуды. Всё о снеге и снежинках Барометр-анероид
Барометр-анероид Ядерный реактор
Ядерный реактор Плавание тел в жидкости
Плавание тел в жидкости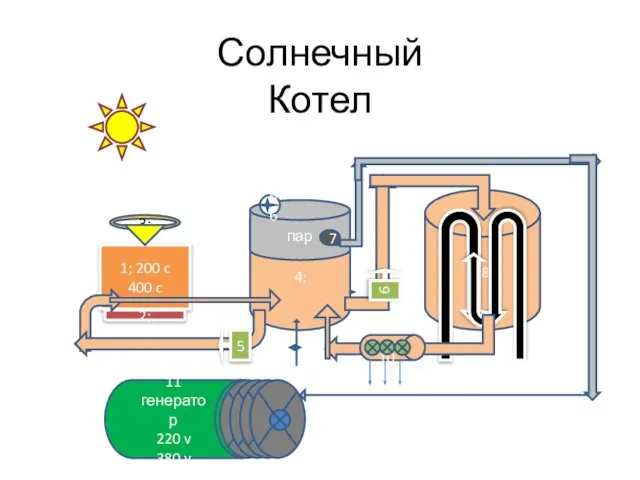 Солнечный котел
Солнечный котел Оксид кремния и маскирующие слои на его основе
Оксид кремния и маскирующие слои на его основе Итоговая контрольная работа. (7 класс)
Итоговая контрольная работа. (7 класс) Карданные передачи. Часть 1
Карданные передачи. Часть 1 Широкополосный генератор подавления радиосигналов
Широкополосный генератор подавления радиосигналов Линзы. Оптическая сила линзы. 9 класс
Линзы. Оптическая сила линзы. 9 класс Динамика. Масса и сила
Динамика. Масса и сила Вопросы для аттестации. Квантовая теория
Вопросы для аттестации. Квантовая теория Презентация по физике "Энергия ядра. Взгляд в будущее" -
Презентация по физике "Энергия ядра. Взгляд в будущее" -