Интерференция, дифракция, поляризация

Принцип Гюйгенса
Волновая теория света основана на принципе Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн даёт положение волнового фронта в последующий момент времени
На основе волновой теории удалось правильно объяснить законы отражения и преломления света

Интерференция
При соблюдении некоторых условий наблюдается отклонение от закона независимости световых пучков. Действие, производимое несколькими световыми лучами отличается от суммы воздействий всех лучей. Такое явление называется интерференцией
При интерференции происходит увеличение средней интенсивности света в одних областях и уменьшение в других

Интерференция света (от лат. inter – взаимно, между собой и ferio – ударяю, поражаю) – пространственное перераспределение энергии света при наложении двух или нескольких световых волн.
Интерференция волн – одно из основных свойств волн любой природы (упругих, электромагнитных, в т.ч. световых и др.). Такие характерные волновые явления, как излучение, распространение и дифракция, тоже связаны с интерференцией. Интерференцией света объясняются окраска тонких масляных пленок на поверхности воды, металлический отлив в окраске крыльев насекомых и птиц, появление цветов побежалости на поверхности металлов, голубоватый цвет просветленных линз оптических приборов и пр.
Некоторые явления интерференции света исследовались еще И. Ньютоном в XVII в., но не могли быть им объяснены с точки зрения его корпускулярной теории. Правильное объяснение интерференции света как типично волнового явления было дано в начале XIX в. Т. Юнгом и О. Френелем.

Когерентность и монохроматичность
Необходимыми условиями возникновения интерференции являются монохроматичность и когерентность световых потоков
Монохроматичность световых волн означает неизменность во времени их длин и частот колебаний
Любой световой поток можно представить как суперпозицию монохроматичных волн

Когерентность и монохроматичность
Интерферировать между собой могут только монохроматические составляющие нескольких световых потоков. При этом суммарная интерференционная картина является наложением всех монохроматических интерференционных картин

Когерентность и монохроматичность
Строго монохроматическое излучение получить невозможно
При излучении света одной длины волны источником, происходит случайное изменение фазы колебаний, это приводит к случайным быстрым изменениям интерференционной картины. Инерционный фоточувствительный прибор при этом не успевает регистрировать её

Когерентность и монохроматичность
Стабильную интерференционную картину можно получить используя когерентные источники
Когерентность источников излучения означает, что колебательные процессы протекают в них согласованно во времени

Когерентность и монохроматичность
Когерентное излучение можно получить двумя способами
От нескольких независимых источников света высокой степени монохроматичности (лазеров)
Выделяя лучи от одного и того же источника
Второй способ получил наибольшее распространение

Волновые свойства света наиболее отчетливо обнаруживают себя в интерференции и дифракции.
Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления:

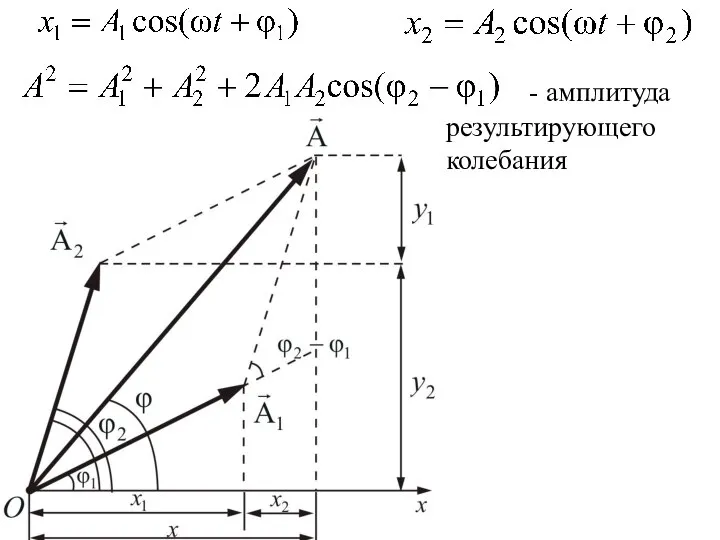
- амплитуда результирующего колебания

Если разность фаз колебаний возбужденных волнами в некоторой точке пространства остается постоянной во времени, то такие волны называются когерентными.
В случае некогерентных волн разность фаз
непрерывно изменяется.

В случае когерентных волн
Последнее слагаемое в этом выражении
-интерференционный член.
,
; в минимуме
, интенсивность
где
; в максимуме
Интенсивность световой волны J равна квадрату амплитуды А. Тогда суммарная интенсивность:

Для некогерентных источников интенсивность результирующей волны всюду одинакова и, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:
Некогерентность естественных источников света обусловлена тем, что излучение тела слагается из волн, хаотически испускаемых многими атомами.
Фазы каждого цуга волны, испускаемого отдельным атомом никак не связаны друг с другом. Атомы излучают хаотически.

Периодическая последовательность горбов и впадин волны и образующиеся в процессе акта излучения одного атома, называется цугом волн или волновым цугом.
Процесс излучения одного цуга атома длится
Длина цуга
В одном цуге укладывается примерно
длин волн.

Рисунок 7.3
Первая волна
Разность фаз двух когерентных волн -
Оптическая разность хода -
L – оптическая длина пути; s – геометрическая длина
пути; n – показатель преломления среды.
вторая
Рассмотрим интерференцию двух когерентных волн:

Условие максимума и минимума интерференции:
Если оптическая разность хода равна целому числу длин волн
- условие интерференционного максимума.
Если оптическая разность хода равна полу-целому числу длин волн
- условие интерференционного минимума.

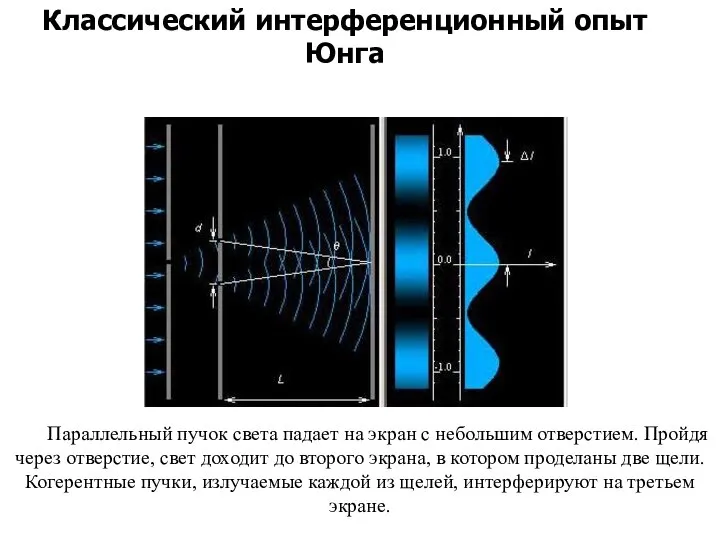
Параллельный пучок света падает на экран с небольшим отверстием. Пройдя через отверстие, свет доходит до второго экрана, в котором проделаны две щели. Когерентные пучки, излучаемые каждой из щелей, интерферируют на третьем экране.
Классический интерференционный опыт Юнга

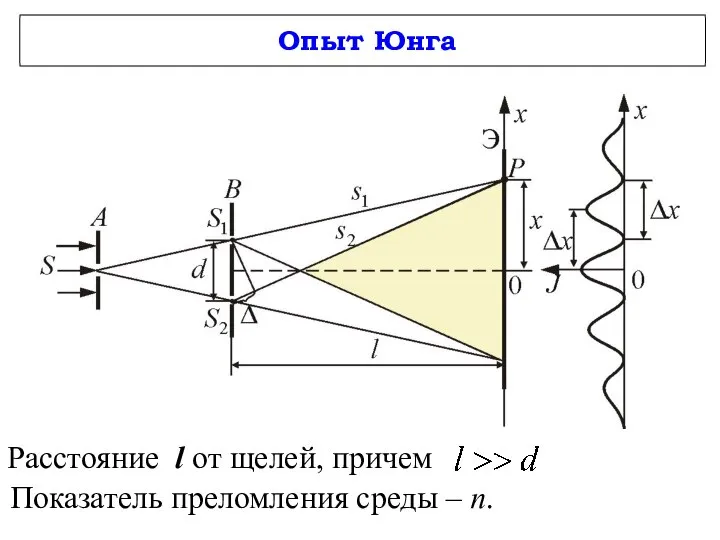
Опыт Юнга
Расстояние l от щелей, причем
Показатель преломления среды – n.

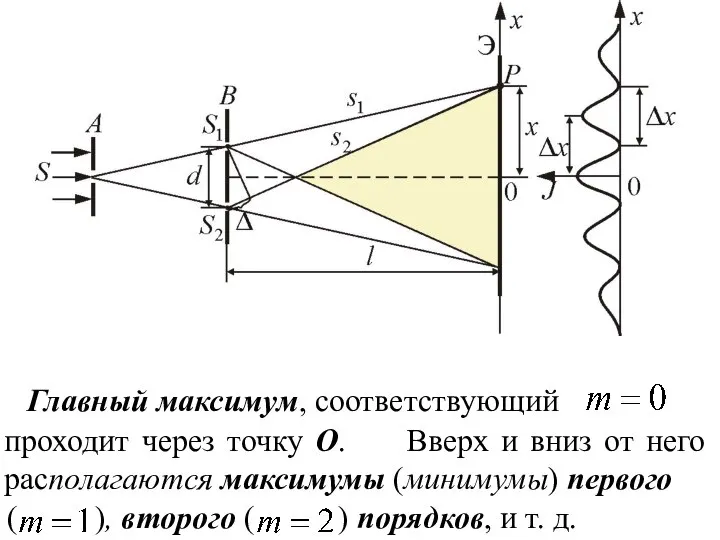
Главный максимум, соответствующий
проходит через точку О. Вверх и вниз от него располагаются максимумы (минимумы) первого
(
), второго (
) порядков, и т. д.

Расстояние между двумя соседними
максимумами (или минимумами) равно
Максимумы интенсивности будут наблюдаться в координатах:
(m = 0, 1, 2, …),
а минимумы – в координатах:
- ширина интерференционной полосы.
Измерив
, зная l и d, можно вычислить длину волны λ. Именно так вычисляют длины волн разных цветов в спектроскопии.

Световые волны одинаковой длины волны, которые приходят в данную точку с постоянной (не изменяющейся со временем) разностью фаз, называются когерентными. Когерентные волны дают неизменную со временем интерференционную картину (распределение интенсивности света в пространстве или на экране.
Область пространства, в которой амплитуда результирующей волны усиливается, называется областью конструктивной интерференции, а в которой ослабляется – деструктивной.

Когерентность и монохроматичность
Необходимым условием интерференции волн является их когерентность, т.е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.
Этому условию удовлетворяют монохроматические волны – волны одной определенной и строго постоянной частоты.

Волну можно приближенно считать монохроматической только в течение времени
где
– время когерентности
За промежуток времени
разность фаз колебаний
изменится на π.
Время когерентности – время, по истечению которого разность фаз волны в некоторой, но одной и той же точке пространства, изменяется на π.

Когерентность колебаний которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временнóй когерентностью.

Два источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию, называются пространственно-когерентными.
Радиусом когерентности (или длиной пространственной когерентности) называется максимальное, поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции.
Пространственная когерентность
ρк – радиус пространственной когерентности;
λ – длина волны;
θ – угловой размер источника.

Условия пространственной когерентности двух волн
1) постоянная во времени разность фаз:
ω1t +φ01 – ω2 t – φ02 = const,
откуда следует
(ω1 – ω2)t + φ01 – φ02 = const.
Это справедливо лишь при
ω1 = ω2
Таким образом, условие постоянства во времени разности фаз эквивалентно условиям одинаковости для когерентных лучей циклических частот в вакууме.
2) соизмеримость амплитуд интерферирующих волн,
3) одинаковое состояние поляризации,
4) лучи, пройдя разные пути, встречаются в некоторой точке пространства.

Интерференция в тонких пленках
Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта.

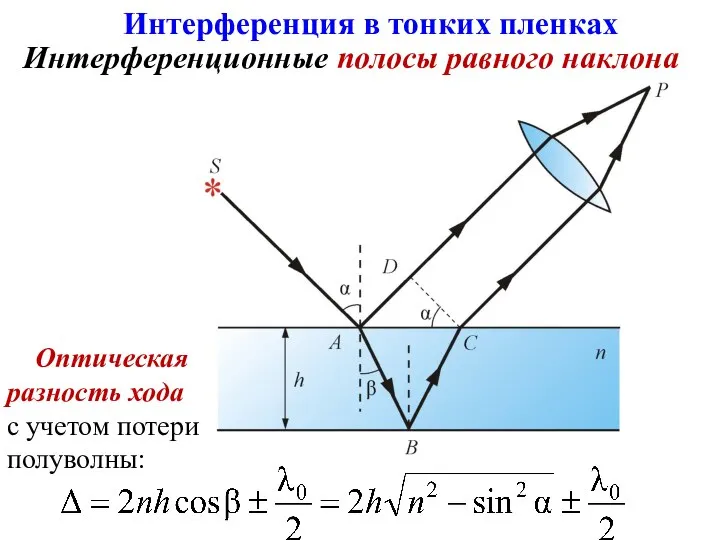
Интерференционные полосы равного наклона
Интерференция в тонких пленках
Оптическая
разность хода
с учетом потери
полуволны:

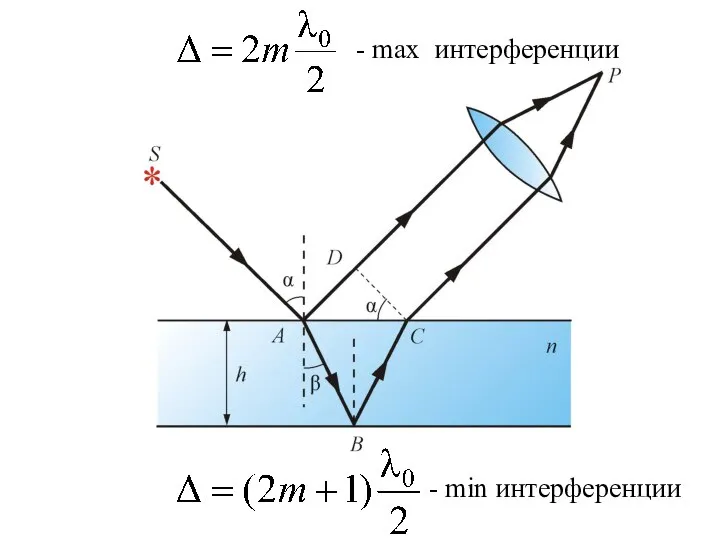
- max интерференции
- min интерференции

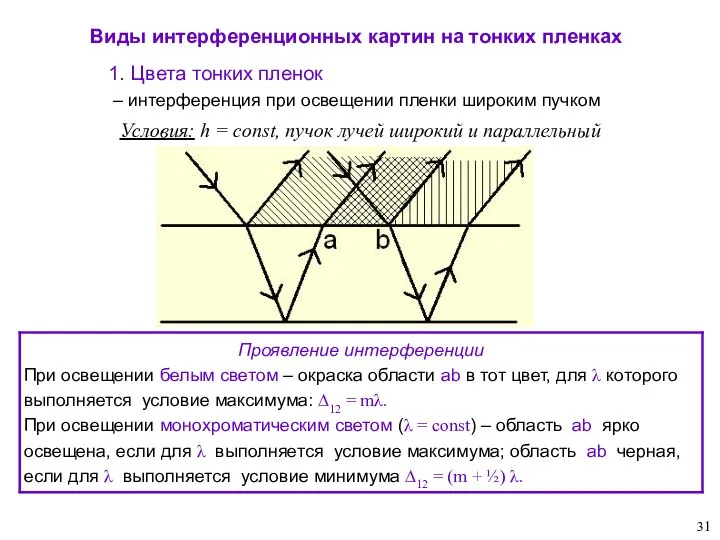
Виды интерференционных картин на тонких пленках
Условия: h = const, пучок лучей широкий и параллельный
1. Цвета тонких пленок
– интерференция при освещении пленки широким пучком

Интерференция от клина.
Полосы равной толщины
В белом свете интерференционные полосы, при отражении от тонких пленок - окрашены. Поэтому такое явление называют цвета тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.

Опыты с мыльной пленкой

Изменение картины интерференции по мере уменьшения толщины мыльной пленки

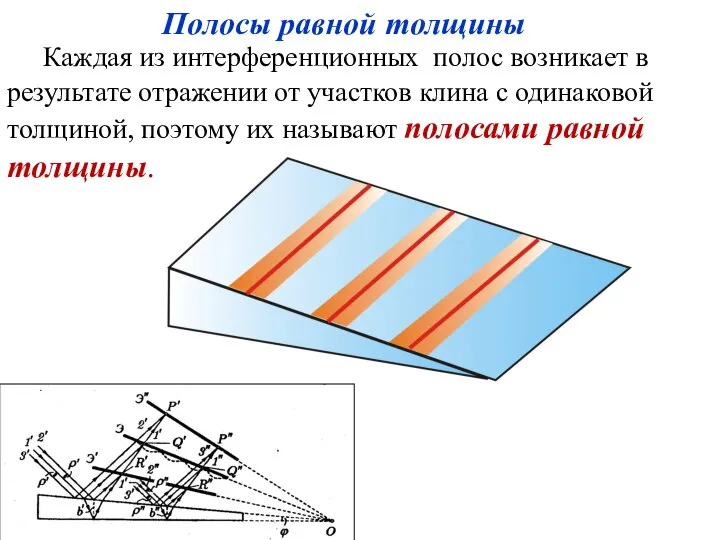
Каждая из интерференционных полос возникает в результате отражении от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
Рис. 7.15
Полосы равной толщины

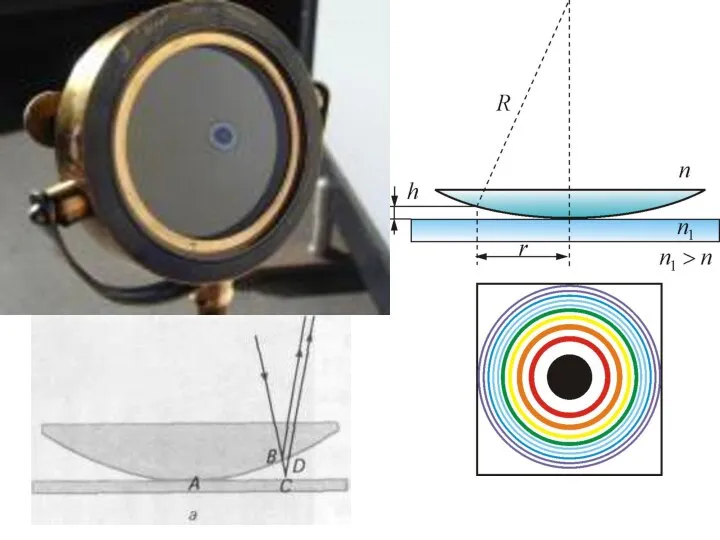
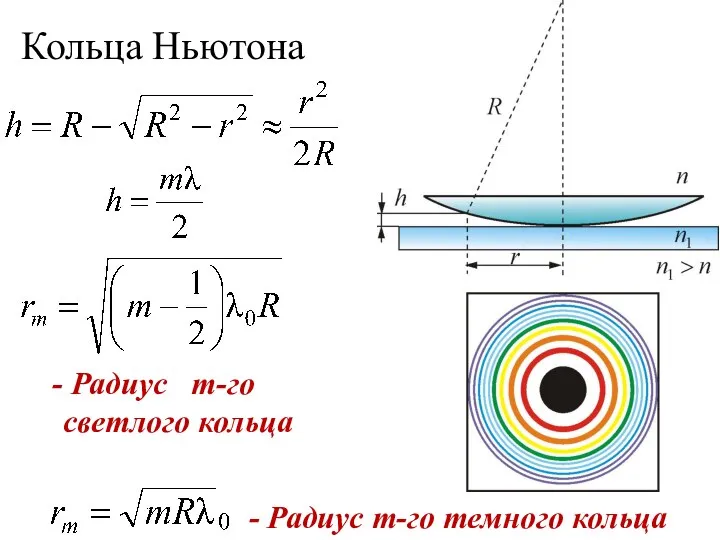
Кольца Ньютона
Ньютон объяснил это явление на основе корпускулярной теории света.
Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре
между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла, называют кольцами Ньютона.

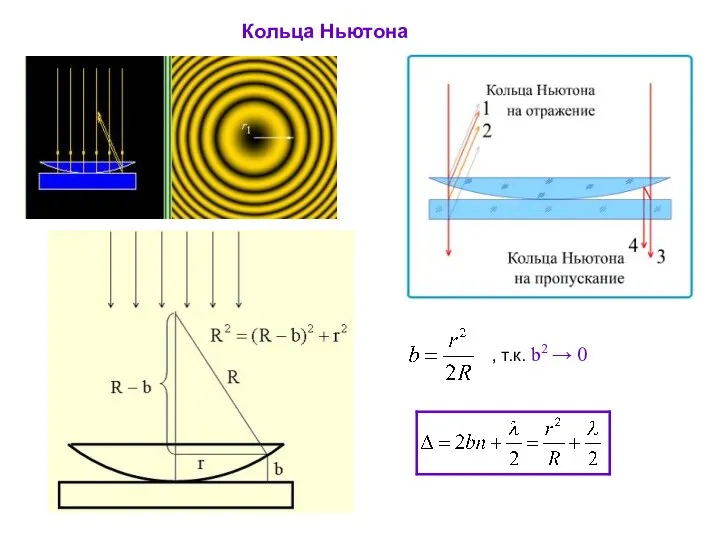
Кольца Ньютона
- Радиус m-го темного кольца
Радиус m-го
светлого кольца

Кольца Ньютона
, т.к. b2 → 0

Условие максимума (светлые кольца) ∆ = m λ, где m – целое число.
- радиус m-го светлого кольца в отраженном свете
(и темного – в прошедшем)
Условие минимума (темные кольца) ∆ = (m + ½) λ.
- радиус m-го темного кольца в отраженном свете
(и светлого – в прошедшем)
Кольца Ньютона в зеленом и красном свете
Пример применения – проверка качества шлифовки линз.

Использование интерференции
Явление интерференции нашло широкое практическое применение
Создание просветлённых покрытий
Измерение малых расстояний и перемещений
Контроль поверхности
Измерение показателя преломления
Голография

Применение интерференции света
1. Тот факт, что расположение интерференционных полос зависит от длины волны и разности хода лучей, позволяет по виду интерференционной картины (или их смещению) проводить точные измерения расстояний при известной длине волны или, наоборот, определять спектр интерферирующих волн (интерференционная спектроскопия).

2. По интерференционной картине можно выявлять и измерять неоднородности среды (в т.ч. фазовые), в которой распространяются волны, или отклонения формы поверхности от заданной.

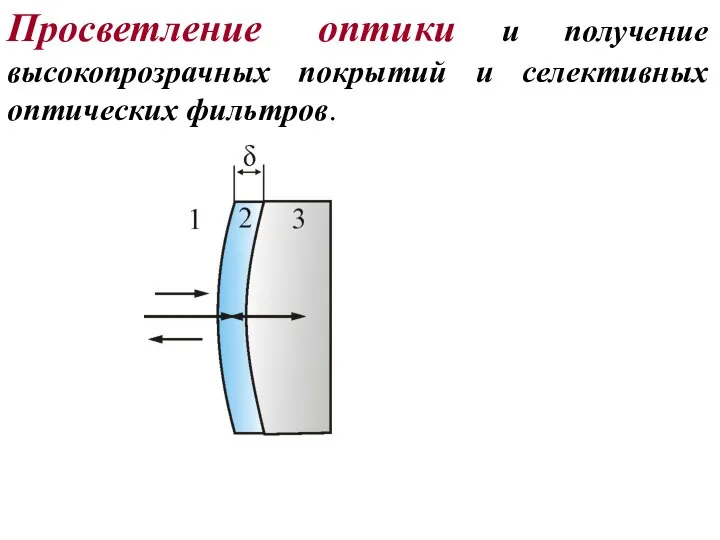
Просветление оптики и получение высокопрозрачных покрытий и селективных оптических фильтров.

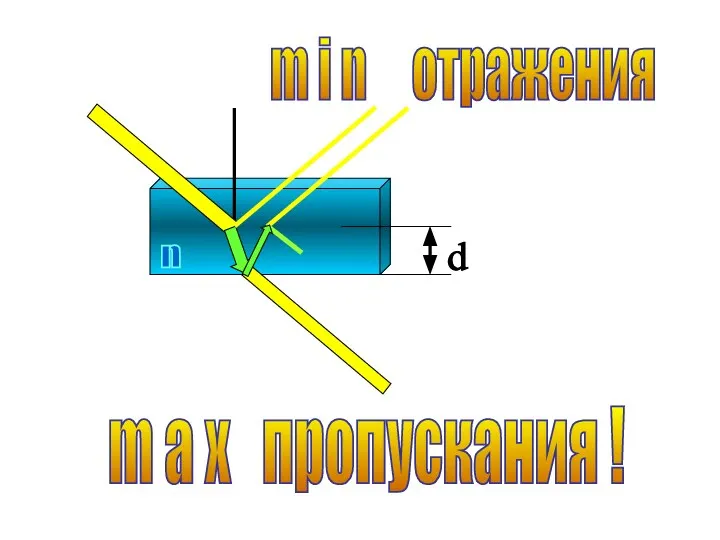
m i n отражения
m a x пропускания !

m a x пропускания света в рабочий объем
Просветление линз и солнечных батарей
Min интерференции

Дифракция света
- приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.
Дифракция света сопровождается интерференцией.
Интерферируют волны, обогнувшие препятствие (опыт Юнга).

Дифракционная картина – система чередующихся светлых и темных колец, если препятствие круг или отверстие.
Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

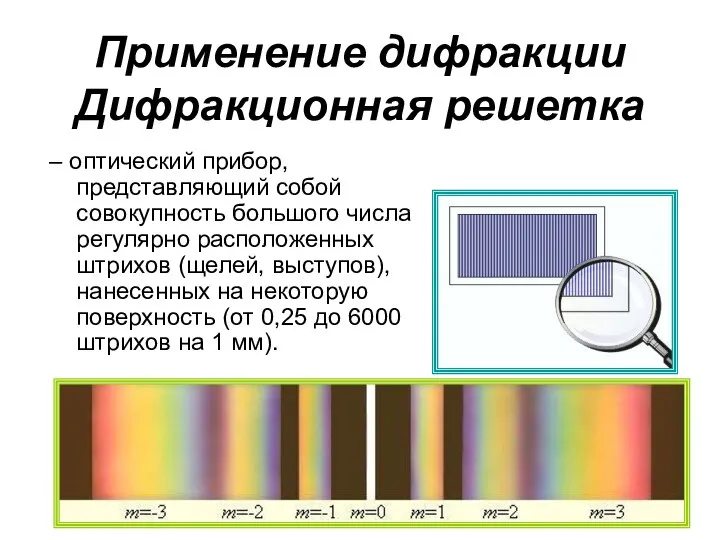
Применение дифракции
Дифракционная решетка
– оптический прибор, представляющий собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесенных на некоторую поверхность (от 0,25 до 6000 штрихов на 1 мм).

Применение дифракции
Дифракционная решетка
Существуют отражательные и прозрачные дифракционные решетки.
Дифракционные решетки используются для разложения электромагнитного излучения в спектр.

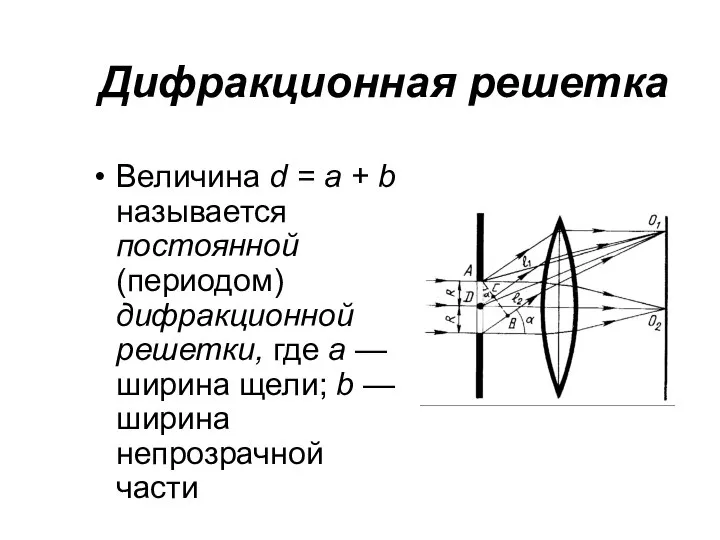
Дифракционная решетка
Величина d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части

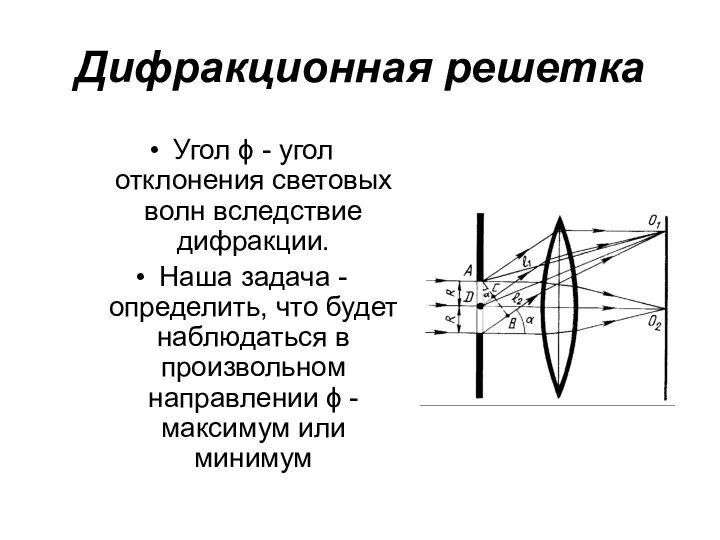
Дифракционная решетка
Угол ϕ - угол отклонения световых волн вследствие дифракции.
Наша задача - определить, что будет наблюдаться в произвольном направлении ϕ - максимум или минимум

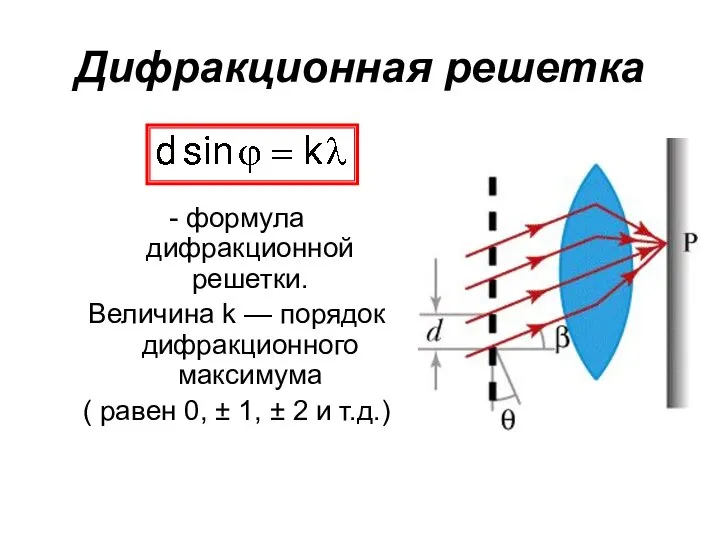
Дифракционная решетка
- формула дифракционной решетки.
Величина k — порядок дифракционного максимума
( равен 0, ± 1, ± 2 и т.д.)

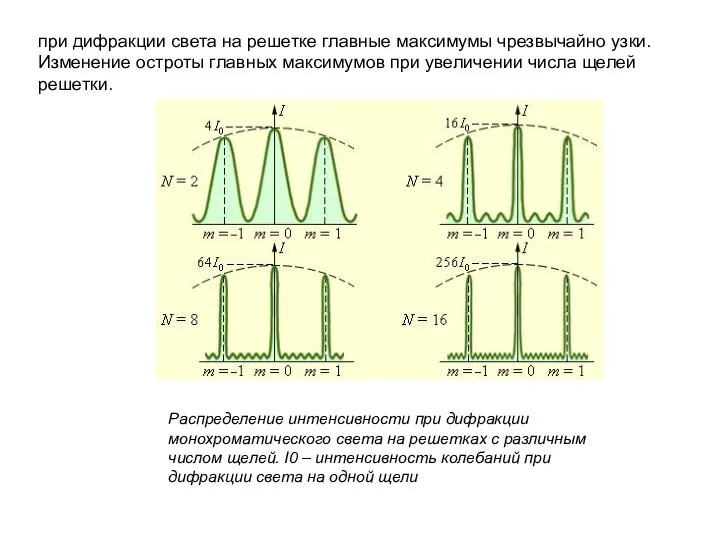
при дифракции света на решетке главные максимумы чрезвычайно узки. Изменение остроты главных максимумов при увеличении числа щелей решетки.
Распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I0 – интенсивность колебаний при дифракции света на одной щели

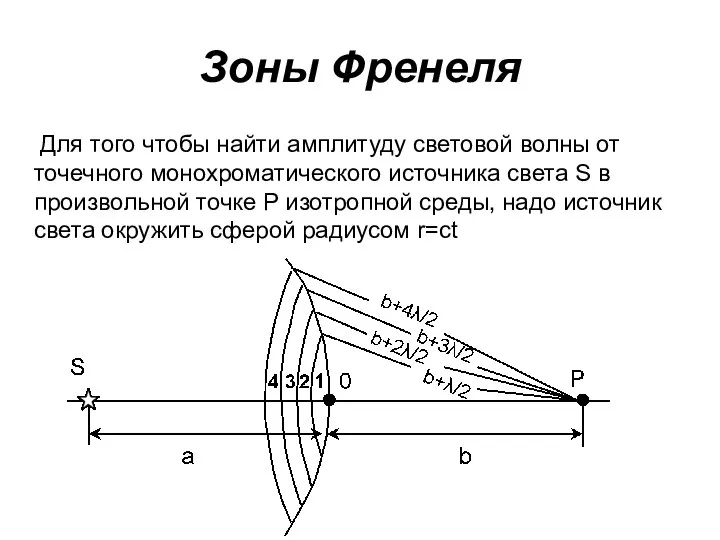
Зоны Френеля
Для того чтобы найти амплитуду световой волны от точечного монохроматического источника света S в произвольной точке P изотропной среды, надо источник света окружить сферой радиусом r=ct

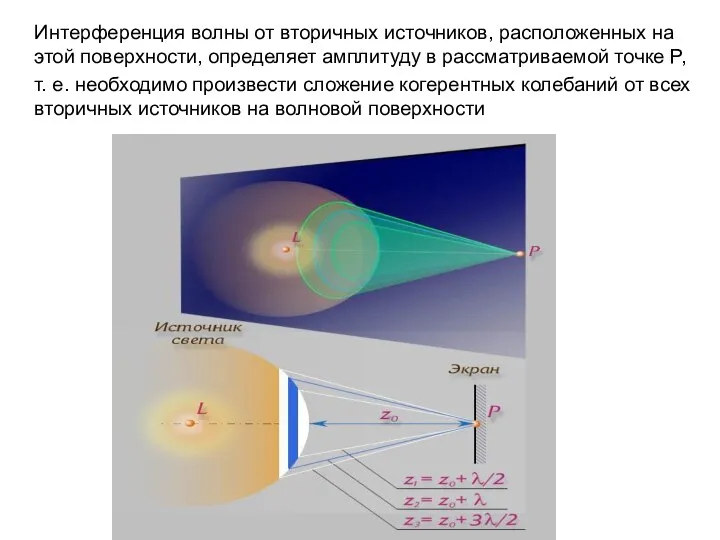
Интерференция волны от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке P,
т. е. необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности

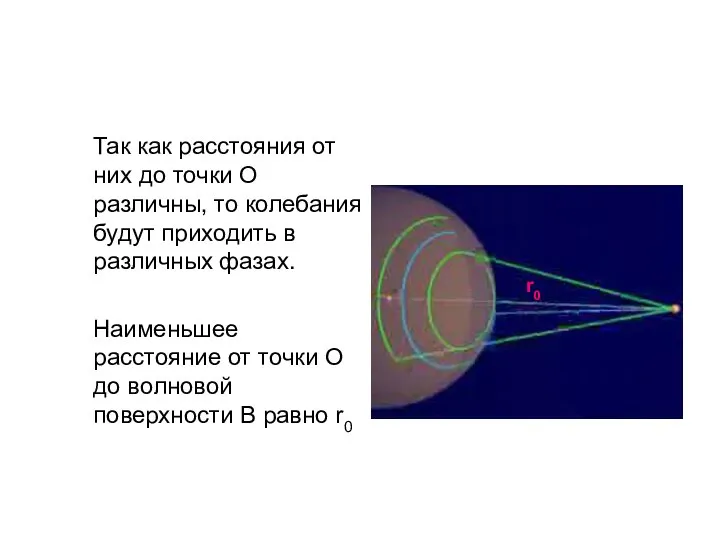
Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах.
Наименьшее расстояние от точки О до волновой поверхности В равно r0
r0

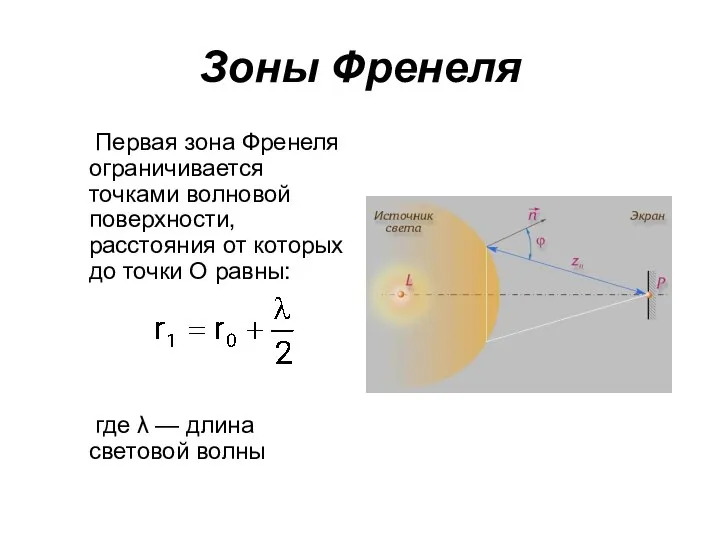
Зоны Френеля
Первая зона Френеля ограничивается точками волновой поверхности, расстояния от которых до точки О равны:
где λ — длина световой волны

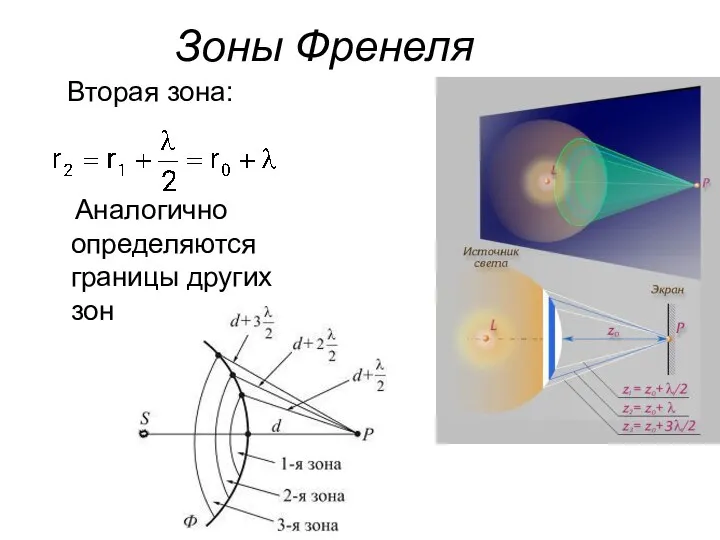
Зоны Френеля
Вторая зона:
Аналогично определяются границы других зон

Если разность хода от двух соседних зон равна половине длины волны, то колебания от них приходят в точку О в противоположных фазах и наблюдается интерференционный минимум, если разность хода равна длине волны, то наблюдается интерференционный максимум

Поляризация света
В поперечной волне колебания могут происходить в любых направлениях, лежащих в плоскости, перпендикулярной направлению распространения волны. Если направления колебаний при этом беспорядочно меняются, но амплитуды их во всех направлениях одинаковы, то такая волна называется естественной.
Если колебания происходят только в одном постоянном направлении, то такая волна называется поляризованной. Если колебания происходят в различных направлениях, но в определенных направлениях амплитуды колебаний больше, чем в других – частично поляризованная волна.
Искусственную поляризацию можно осуществить, пропуская волну через поляризатор.

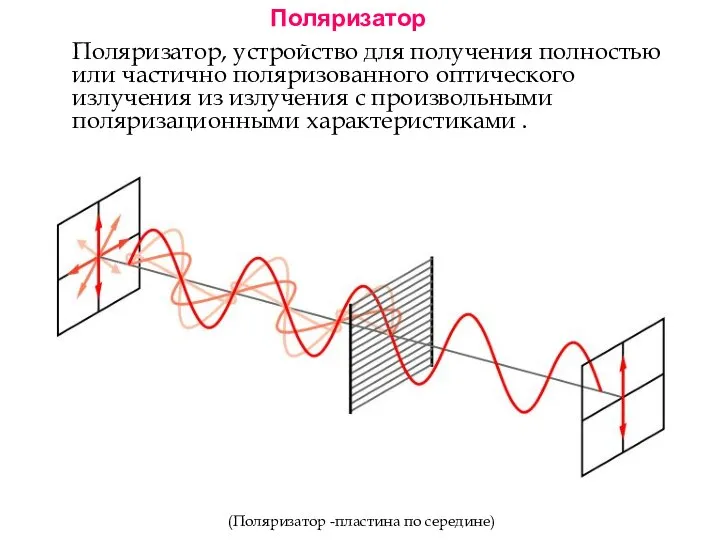
Поляризатор, устройство для получения полностью или частично поляризованного оптического излучения из излучения с произвольными поляризационными характеристиками .
(Поляризатор -пластина по середине)
Поляризатор

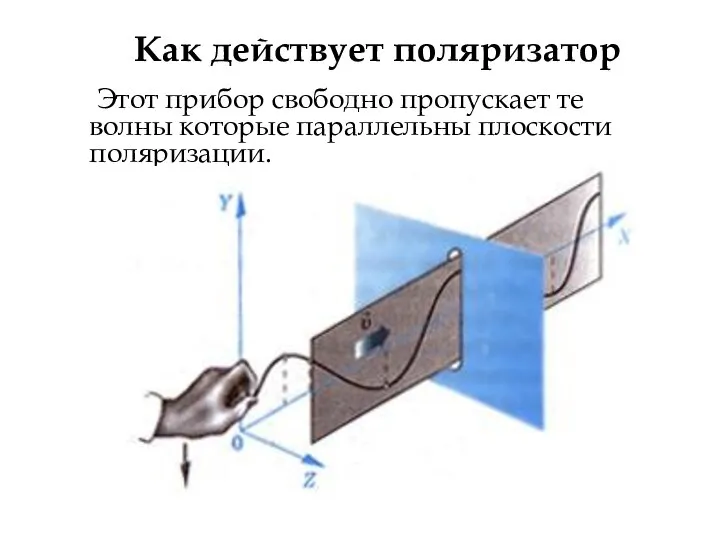
Этот прибор свободно пропускает те волны которые параллельны плоскости поляризации.
Как действует поляризатор

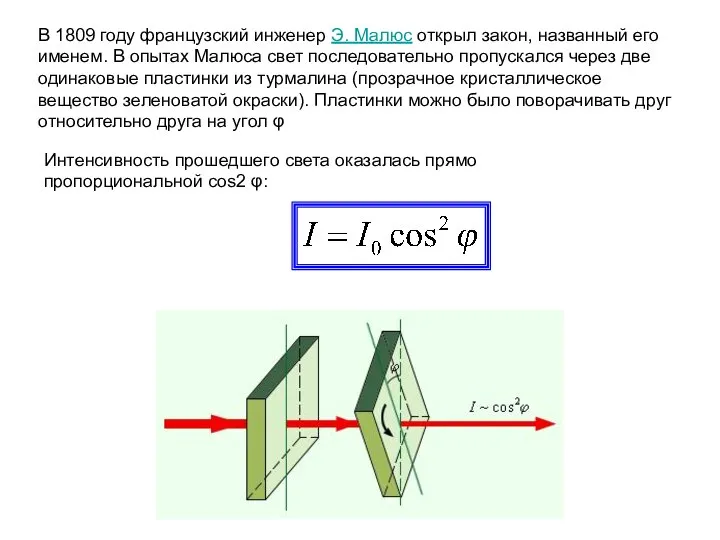
В 1809 году французский инженер Э. Малюс открыл закон, названный его именем. В опытах Малюса свет последовательно пропускался через две одинаковые пластинки из турмалина (прозрачное кристаллическое вещество зеленоватой окраски). Пластинки можно было поворачивать друг относительно друга на угол φ
Интенсивность прошедшего света оказалась прямо пропорциональной cos2 φ:

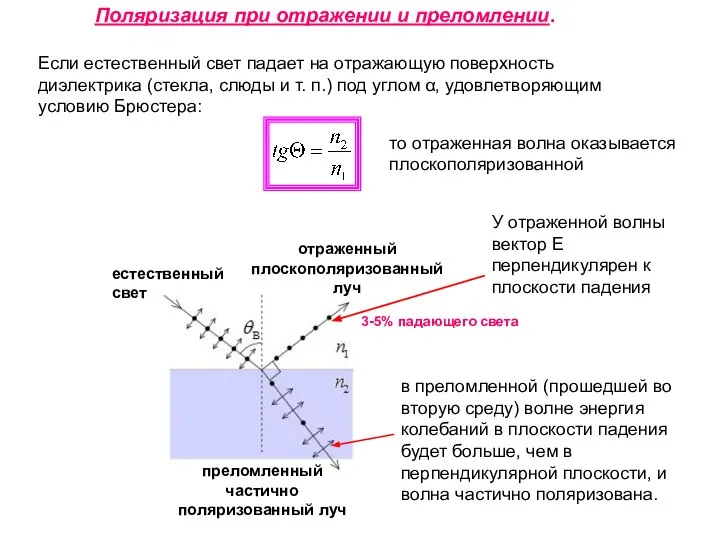
Поляризация при отражении и преломлении.
Если естественный свет падает на отражающую поверхность диэлектрика (стекла, слюды и т. п.) под углом α, удовлетворяющим условию Брюстера:
то отраженная волна оказывается плоскополяризованной
3-5% падающего света
У отраженной волны вектор Е перпендикулярен к плоскости падения
в преломленной (прошедшей во вторую среду) волне энергия колебаний в плоскости падения будет больше, чем в перпендикулярной плоскости, и волна частично поляризована.

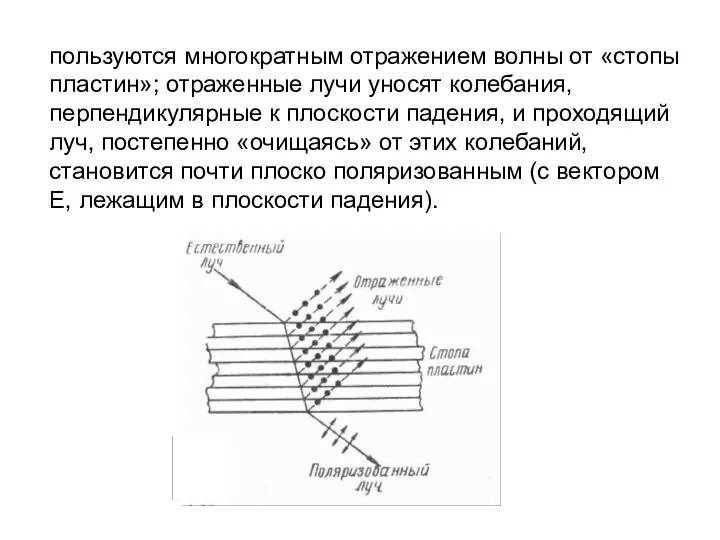
пользуются многократным отражением волны от «стопы пластин»; отраженные лучи уносят колебания, перпендикулярные к плоскости падения, и проходящий луч, постепенно «очищаясь» от этих колебаний, становится почти плоско поляризованным (с вектором Е, лежащим в плоскости падения).

Поляризация при двойном лучепреломлении в кристаллах
Обыкновенный и необыкновенный лучи имеют в кристалле различные скорости распространения, следовательно, различные показатели преломления n0 и nе; этим объясняется двойное лучепреломление в точке падения волны на грань призмы
Это явление наблюдается в оптически анизотропной среде, если ее оптические свойства (скорость распространения света или показатели преломления) различны в различных направлениях.
в кристаллах существует одно или несколько направлений, вдоль которых скорость света не зависит от ориентировки вектора Е. Эти направления называются оптическими осями кристалла.
Так как вектор Е перпендикулярен к своему лучу, то при распространении света вдоль оптической оси вектор Е при всех его различных ориентировках в пространстве всегда перпендикулярен также и к оптической оси.

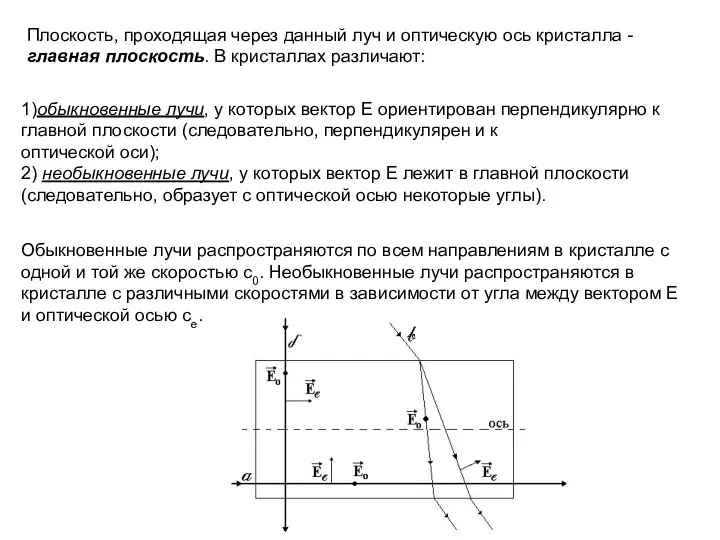
Плоскость, проходящая через данный луч и оптическую ось кристалла - главная плоскость. В кристаллах различают:
1)обыкновенные лучи, у которых вектор Е ориентирован перпендикулярно к главной плоскости (следовательно, перпендикулярен и к
оптической оси);
2) необыкновенные лучи, у которых вектор Е лежит в главной плоскости (следовательно, образует с оптической осью некоторые углы).
Обыкновенные лучи распространяются по всем направлениям в кристалле с одной и той же скоростью с0. Необыкновенные лучи распространяются в кристалле с различными скоростями в зависимости от угла между вектором Е и оптической осью се.