Слайд 22.3. Кинематические характеристики движения.

Слайд 4Перемещение в координатном виде.

Слайд 5Перемещение при малом промежутке времени.

Слайд 7Элемент
В физике элементом какой либо физической величины называется такое достаточно малое изменение

этой величины, которое по условиям задачи можно считать бесконечно малым по отношению к другим значениям этой величины. Элементы физических величин обозначают обозначениями самой этой величины с добавлением латинской буквы d слева от обозначения величины. Таким образом, dt есть обозначение бесконечно малого промежутка времени, т.е. элементарного промежутка или элемента времени.
Слайд 9Проекция элементарного перемещения на вектор касательной.

Слайд 14Направление мгновенной скорости.

Слайд 172.6. Ускорение в криволинейном движении. Нормальное и тангенциальное ускорение.

Слайд 18Ускорение при криволинейном движении.

Слайд 19Тангенциальное ускорение.
Отсюда видно, что ускорение в общем случае состоит из двух слагаемых.

Первое слагаемое называется тангенциальным ускорением. Оно направлено по касательной, о чём говорит направление единичного вектора касательной. Если модуль скорости убывает, производная от касательной проекции скорости по времени отрицательна, и тангенциальное ускорение направлено против скорости, в противном случае - по вектору скорости.
Слайд 20Направление тангенциального ускорения.

Слайд 23Типы переменного движения.
Если ускорение есть нуль, движение равномерное, если ускорение константа –

движение равнопеременное, если тангенциальное ускорение нуль, движение равномерно по траектории, если константа – движение равнопеременное по траектории.
Слайд 24Замедленные и ускоренные движения.
При этом если скорость и тангенциальное ускорение совпадают по

направлению, скорость растёт, и движение называется ускоренным. Если скорость и тангенциальное ускорение противоположны, скорость убывает, и движение называется замедленным.
Слайд 252.7. Перемещение в различных движениях, законы различных движений.

Слайд 28Закон равномерного движения в координатном виде.

Слайд 30Скорость при постоянном ускорении.

Слайд 31Равноускоренное и равнозамедленное движение.
Если скорость сонаправлена с ускорением, движение называется равноускоренным, в

противном случае – равнозамедленным.
Слайд 33Закон изменения скорости в координатном виде.

Слайд 34Закон равнопеременного движения.

Слайд 35Закон равнопеременного движения в координатном виде.

Слайд 39Движение тела, брошенного под углом к горизонту.Progr

Слайд 40Progr D: Progr E: Progr F: Progr G:

Слайд 412.9. Колебательное движение.
Примером переменного движения могут служить гармонические колебания.
Progr D: Progr

E: Progr F: Progr G:
Определение. Периодическими движениями материальной точки называются такие движения, при которых она в каждую точку своей траектории постоянно возвращается через равные промежутки времени.
Слайд 43Механические колебания.
Определение. Механическими колебаниями материальной точки называются такие периодические движения материальной точки

между двумя крайними точками пространства, при которых траектория движения материальной точки в одну сторону совпадает с траекторией движения в другую сторону.
Слайд 44Уравнение гармонических колебаний.

Слайд 45Гармонические колебания вдоль одной оси.















































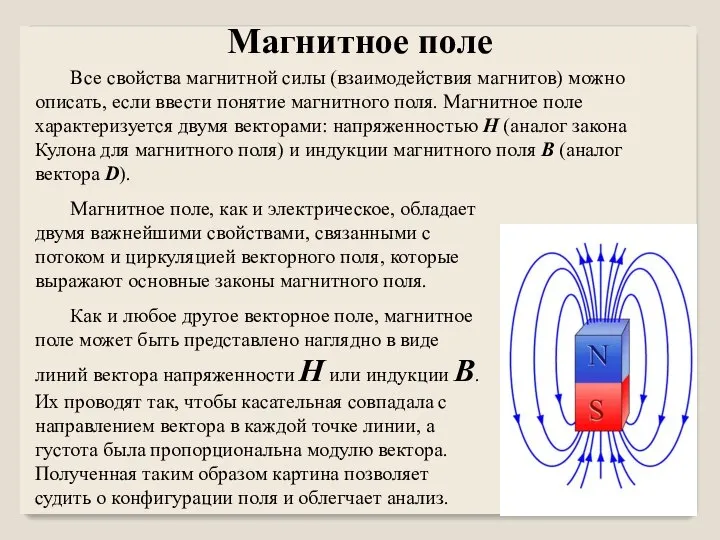 Магнитное поле
Магнитное поле Перемещение при прямолинейном равноускоренном движении. Урок 1
Перемещение при прямолинейном равноускоренном движении. Урок 1 Прискорення. Рівноприскорений рух
Прискорення. Рівноприскорений рух Сила. Сила тяжести
Сила. Сила тяжести Механические и электромагнитные волны
Механические и электромагнитные волны Термодинамические циклы. Второе начало термодинамики. Энтропия. Термодинамические потенциалы
Термодинамические циклы. Второе начало термодинамики. Энтропия. Термодинамические потенциалы Процесстер мен аппараттар
Процесстер мен аппараттар Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2014 года по физике
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2014 года по физике Строение электронных оболочек атомов
Строение электронных оболочек атомов Авиационная связь
Авиационная связь Реактивное движение
Реактивное движение История кинематики
История кинематики Презентация на тему Физика в картинках
Презентация на тему Физика в картинках  Изучение кристаллической структуры материалов
Изучение кристаллической структуры материалов Марковские процессы. Правило
Марковские процессы. Правило Презентация на тему Взаимные превращения жидкости, пара и твёрдого тела
Презентация на тему Взаимные превращения жидкости, пара и твёрдого тела  Магнитная индукция
Магнитная индукция Определение скоростей точек тела при плоскопараллельном движении
Определение скоростей точек тела при плоскопараллельном движении Проводники и диэлектрики в электрическом поле
Проводники и диэлектрики в электрическом поле Основные физические явления, используемые в работе ТСО. Тема 3
Основные физические явления, используемые в работе ТСО. Тема 3 Сравнение идей классической и квантовой физики в объяснении строения атома
Сравнение идей классической и квантовой физики в объяснении строения атома Кинематика твердого тела. Простейшие движения твердого тела
Кинематика твердого тела. Простейшие движения твердого тела Механические колебания. Физика 9 класс
Механические колебания. Физика 9 класс Основные понятия и задачи кинематики (продолжение)
Основные понятия и задачи кинематики (продолжение) Радиоволны. Свойства
Радиоволны. Свойства Энергия связи. Дефект масс
Энергия связи. Дефект масс Определение показателя преломления стекла
Определение показателя преломления стекла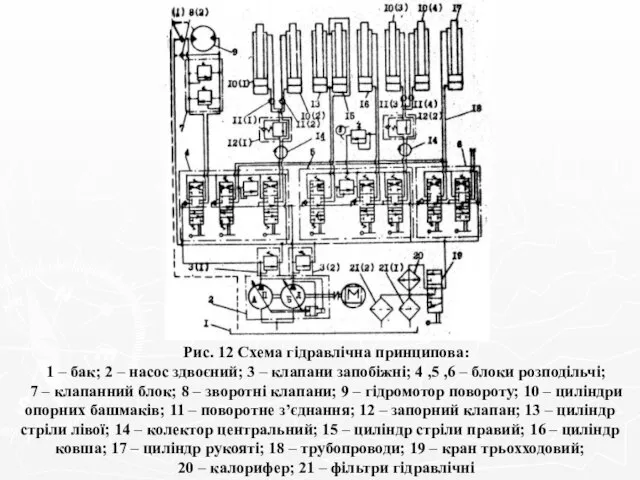 Схема гідравлічна принципова. Билет 7
Схема гідравлічна принципова. Билет 7