Содержание
- 2. Вывод. Ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой - нибудь другой точки
- 3. может быть разложено на нормальное и касательное ускорения Если полюс А движется по криволинейной траектории, то
- 4. обычно удается определить, поэтому для нахождения полного ускорения можно применять метод проекций. Проектируя векторное равенство (3)
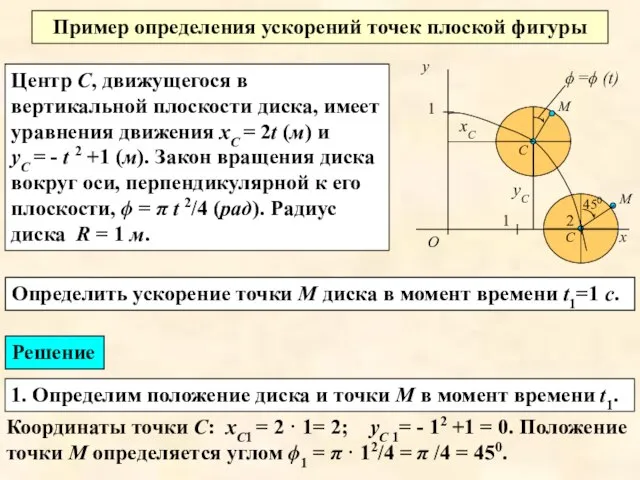
- 5. Центр С, движущегося в вертикальной плоскости диска, имеет уравнения движения хС = 2t (м) и уС
- 6. Для определения ускорения точки М воспользуемся формулой (2), принимая в качестве полюса точку С. Тогда получим
- 7. будет направлен к центру диска, то есть к точке С. /8 = - 0,56, Вектор Проекции
- 9. Скачать презентацию





 Расчет характеристик световой волны. Практическая работа №21
Расчет характеристик световой волны. Практическая работа №21 Движение по окружности
Движение по окружности Решения задач по теме Плавление и отвердевание кристаллических тел
Решения задач по теме Плавление и отвердевание кристаллических тел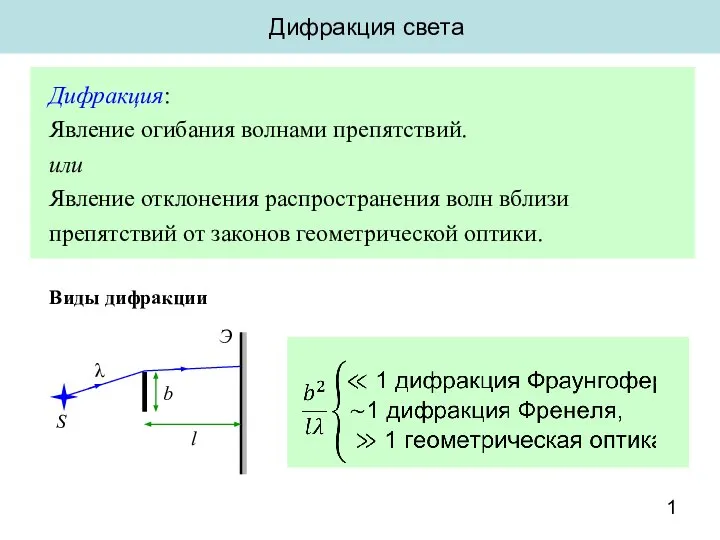 Дифракция света
Дифракция света Давление твердых тел
Давление твердых тел Пара сил. Момент пары сил. Свойства пар сил. Момент силы относительно точки
Пара сил. Момент пары сил. Свойства пар сил. Момент силы относительно точки Подвижной состав автотранспорта
Подвижной состав автотранспорта Презентация на тему Модели атомов. Опыт Резерфорда
Презентация на тему Модели атомов. Опыт Резерфорда  Ремонт центробежного водяного насоса
Ремонт центробежного водяного насоса Источники звука. Звуковые колебания
Источники звука. Звуковые колебания Вихрь (ротор) векторного поля
Вихрь (ротор) векторного поля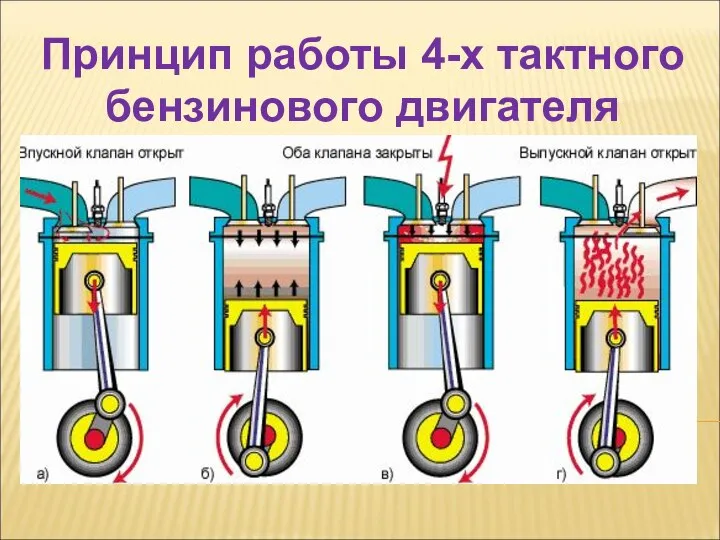 Принцип работы 4-х тактного бензинового двигателя
Принцип работы 4-х тактного бензинового двигателя Цепи периодического несинусоидального тока
Цепи периодического несинусоидального тока Методы измерения потерь в оптических волокнах
Методы измерения потерь в оптических волокнах Электрокинетические явления
Электрокинетические явления Применение интеграла к решению физических задач
Применение интеграла к решению физических задач Разработка и исследование системы управления технологического процесса с помощью термодинамических характеристик
Разработка и исследование системы управления технологического процесса с помощью термодинамических характеристик Электрический ток в газах
Электрический ток в газах Инжекторный ДВС
Инжекторный ДВС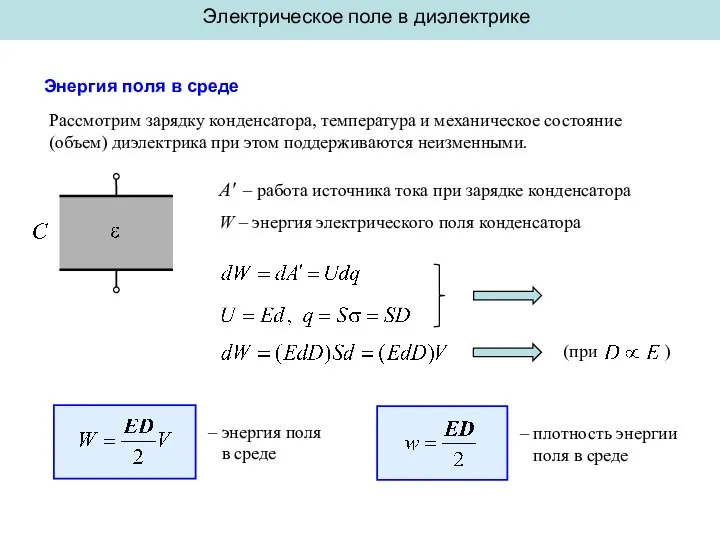 Энергия поля в среде
Энергия поля в среде Презентация на тему Равнодействующая сила
Презентация на тему Равнодействующая сила  Зарождение теории относительности
Зарождение теории относительности Рентгеновское излучение ( Х-лучи )
Рентгеновское излучение ( Х-лучи ) Воль-амперная характеристика полупроводникового диода и лампы нагревания. Лабораторная работа
Воль-амперная характеристика полупроводникового диода и лампы нагревания. Лабораторная работа Радиоактивные превращения атомных ядер. Закон радиоактивного распада
Радиоактивные превращения атомных ядер. Закон радиоактивного распада Флуоресценция. Теория рассеяния. (Тема 14)
Флуоресценция. Теория рассеяния. (Тема 14) Вивчення будови трактора за допомогою каталогу деталей та вузлів на прикладі трактора MF 8470/8480
Вивчення будови трактора за допомогою каталогу деталей та вузлів на прикладі трактора MF 8470/8480 Расчет коленчатого вала. Лекция №11б
Расчет коленчатого вала. Лекция №11б