Содержание
- 2. МЕХАНИКА Наука об общих законах движения тел. ЗАДАЧА МЕХАНИКИ Основной задачей механики является определение положения тела
- 3. Механическое движение Перемещение тела в пространстве относительно других тел с течением времени.
- 4. Разделы классической механики: Кинематика рассматривает описание движения тел. Динамика изучает влияние взаимодействий между телами на их
- 5. Основные понятия кинематики: 1.Материальная точка 2.Система отсчета 3.Перемещение 4.Траектория 5.Путь 6.Скорость
- 6. Материальная точка Тело, размерами которого в данных условиях можно пренебречь, называют материальной точкой.
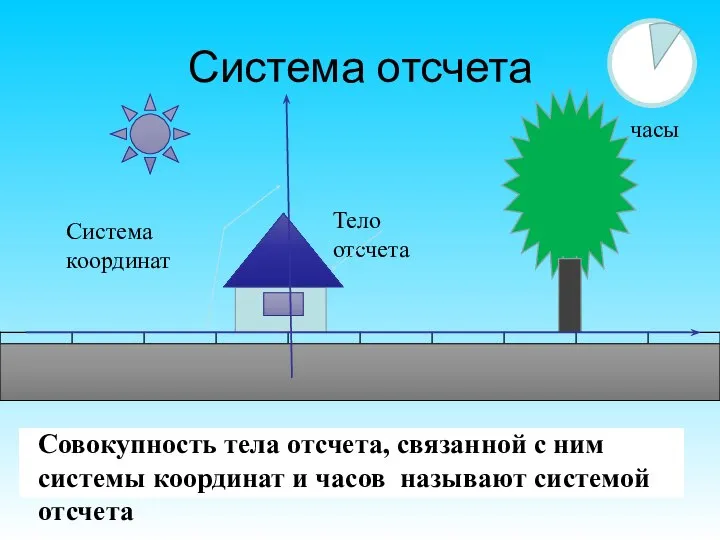
- 7. Система отчета Система отчета состоит из тела отсчета, по отношению к которому описывают движения тел, связанной
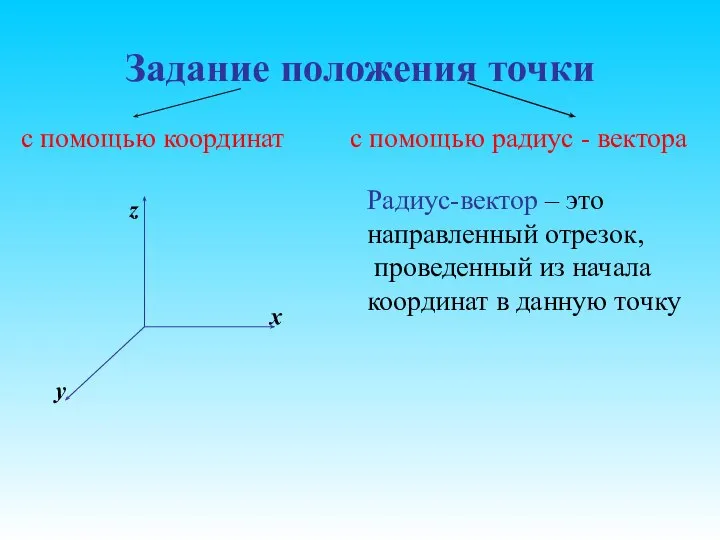
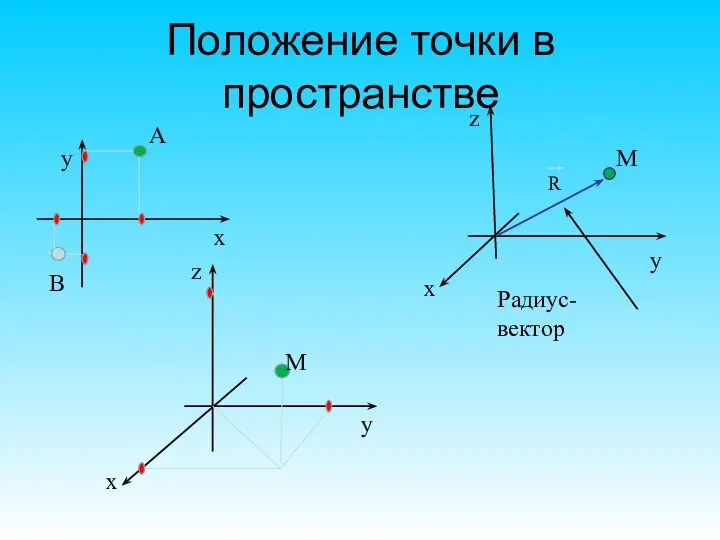
- 8. Задание положения точки с помощью координат с помощью радиус - вектора x y z Радиус-вектор –
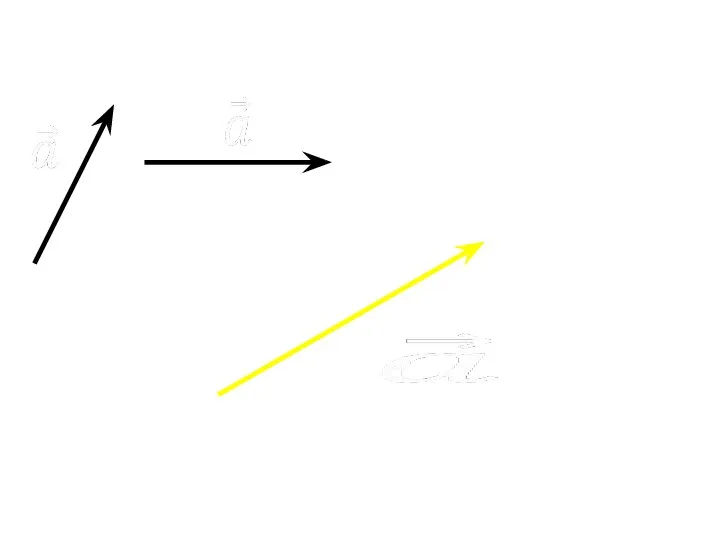
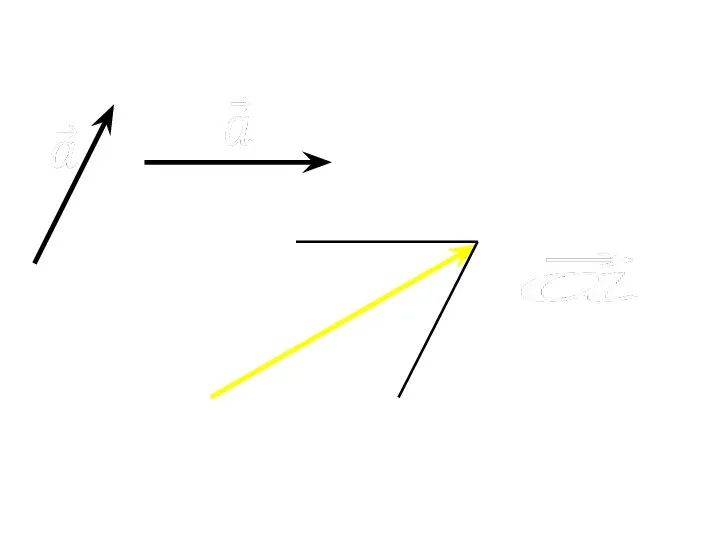
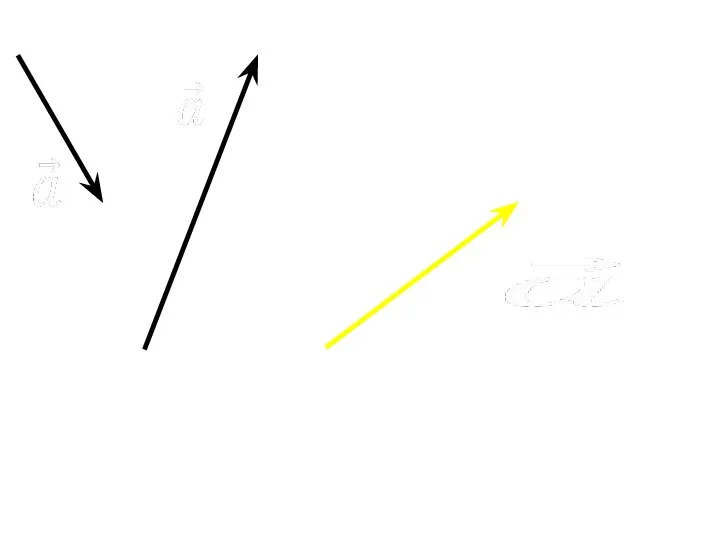
- 9. Правило треугольника СЛОЖЕНИЕ ВЕКТОРОВ
- 11. Правило параллелограмма СЛОЖЕНИЕ ВЕКТОРОВ
- 13. вычитание ВЕКТОРОВ
- 15. Положение точки в пространстве x y z x y x y z
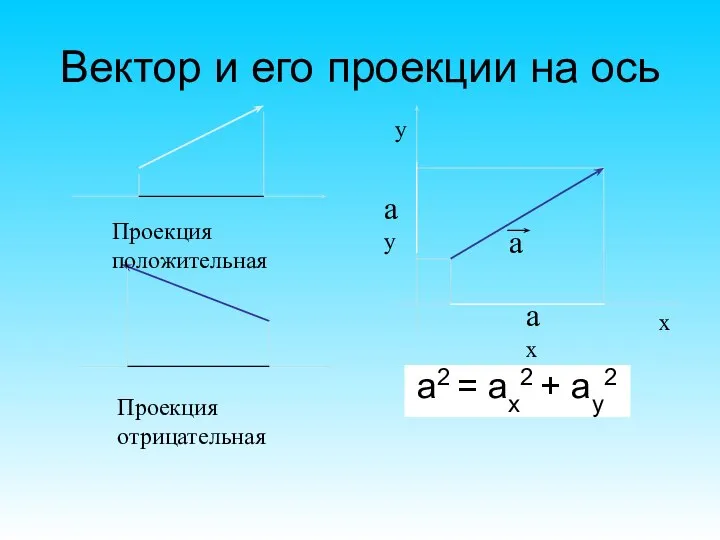
- 16. Вектор и его проекции на ось Проекция положительная Проекция отрицательная х у
- 17. КИНЕМАТИКА Траектория – это воображаемая линия, вдоль которой движется тело. Законом движения называется формула, устанавливающая зависимость
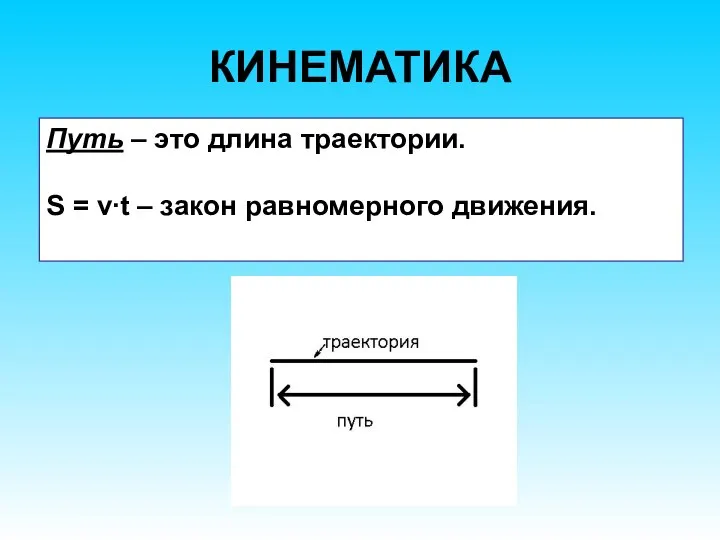
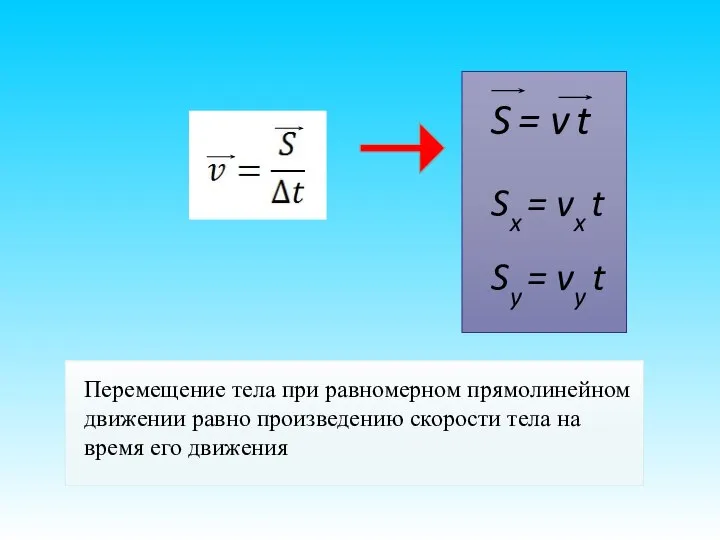
- 18. КИНЕМАТИКА Путь – это длина траектории. S = v∙t – закон равномерного движения.
- 19. КИНЕМАТИКА Всякое движение характеризуется еще следующими величинами: - перемещение; - скорость; - ускорение.
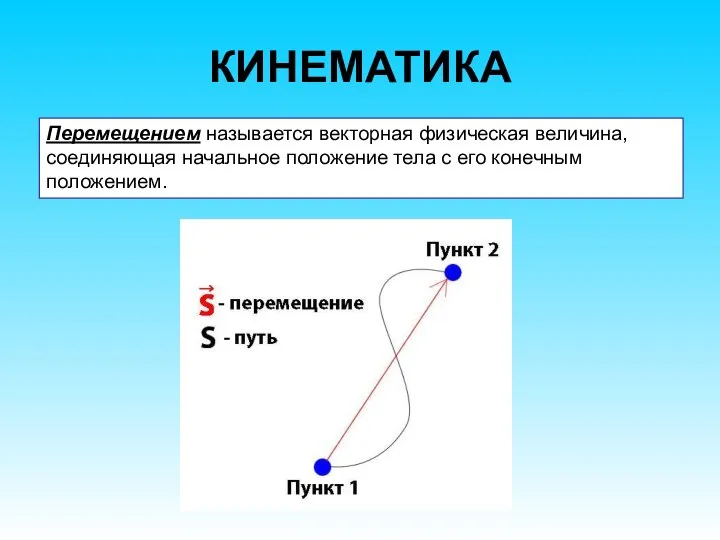
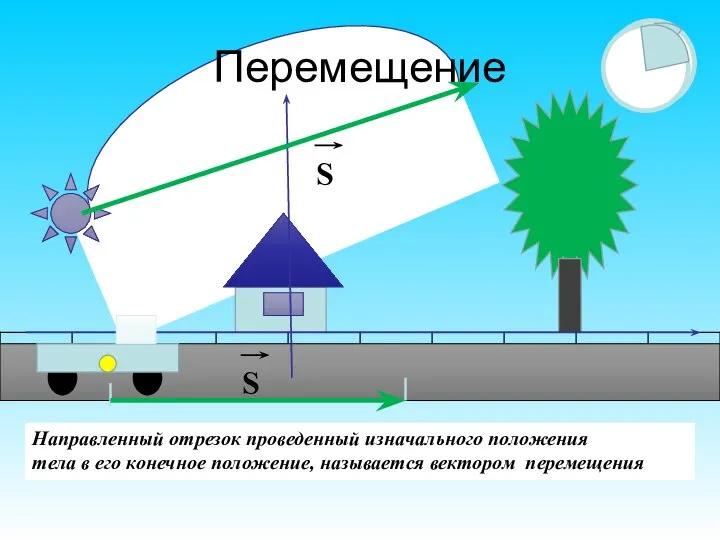
- 20. КИНЕМАТИКА Перемещением называется векторная физическая величина, соединяющая начальное положение тела с его конечным положением.
- 21. Система отсчета
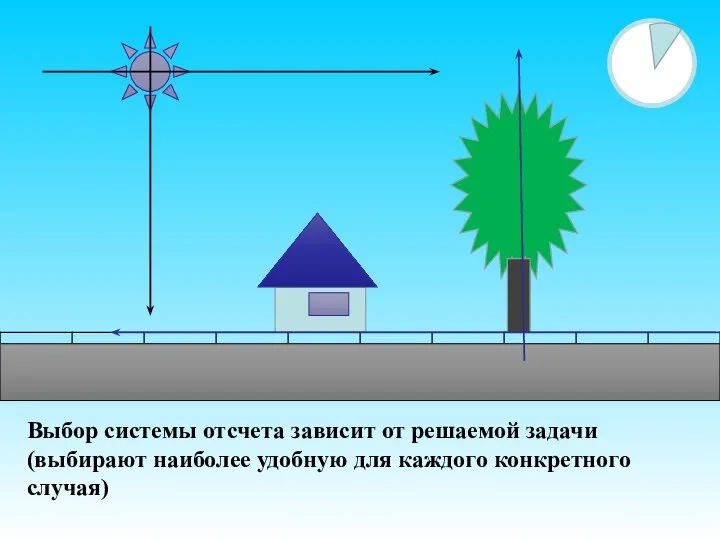
- 22. Выбор системы отсчета зависит от решаемой задачи (выбирают наиболее удобную для каждого конкретного случая)
- 23. Перемещение
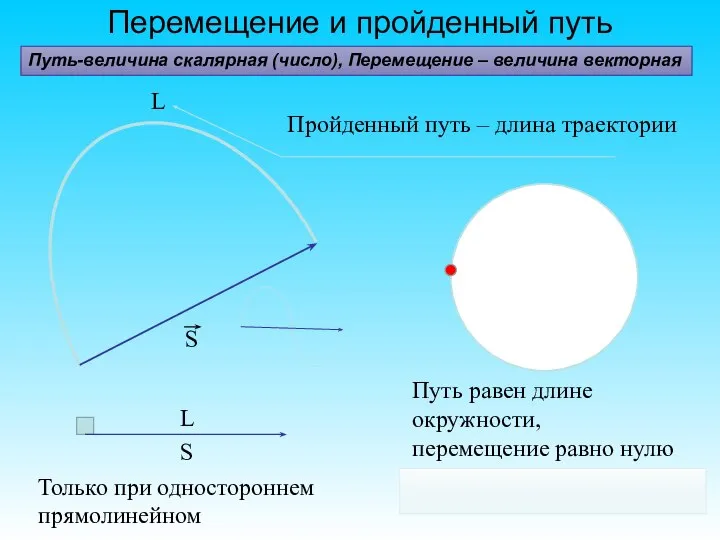
- 24. Перемещение и пройденный путь Пройденный путь – длина траектории Путь равен длине окружности, перемещение равно нулю
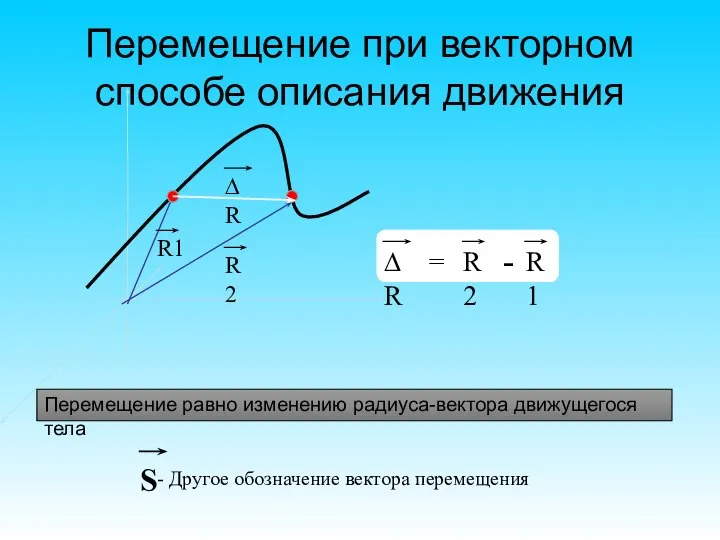
- 25. Перемещение при векторном способе описания движения Перемещение равно изменению радиуса-вектора движущегося тела
- 26. Перемещение вектор, соединяющий начальное положение материальной точки с его конечным положением. Траектория линия, описываемая в пространстве
- 27. КИНЕМАТИКА Скорость – это векторная физическая величина, характеризующая быстроту движения тела. Ускорение – это векторная физическая
- 28. Мгновенная скорость это скорость в каждой конкретной точке траектории в соответствующий момент времени. Средняя скорость величина,
- 29. КИНЕМАТИКА ПРОСТЕЙШИЙ ВИД ДВИЖЕНИЯ: Прямолинейное движение
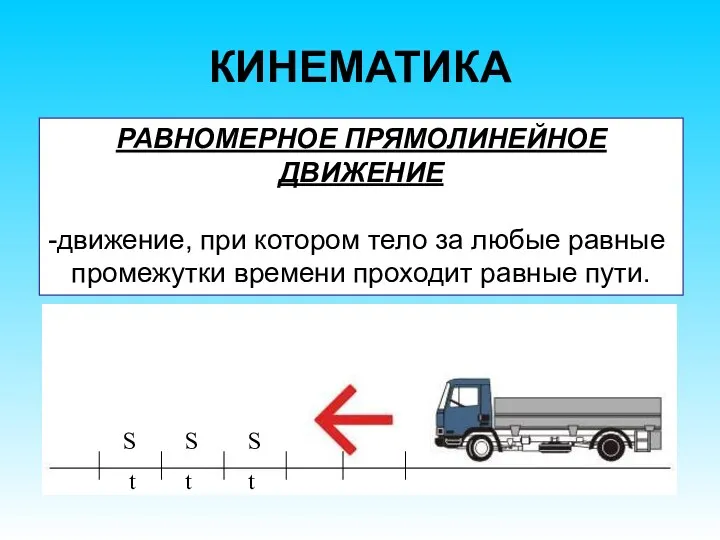
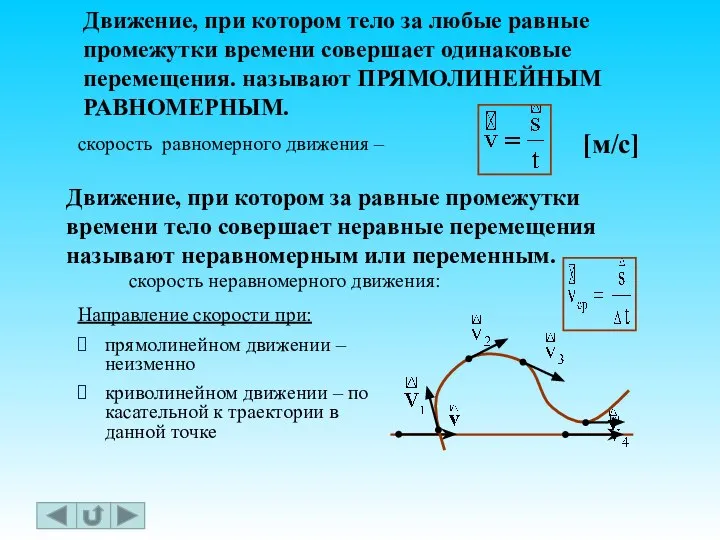
- 30. КИНЕМАТИКА РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ движение, при котором тело за любые равные промежутки времени проходит равные пути.
- 31. Равномерное движение Движение, когда за любые равные промежутки времени тело совершает одинаковые перемещения. Это движение с
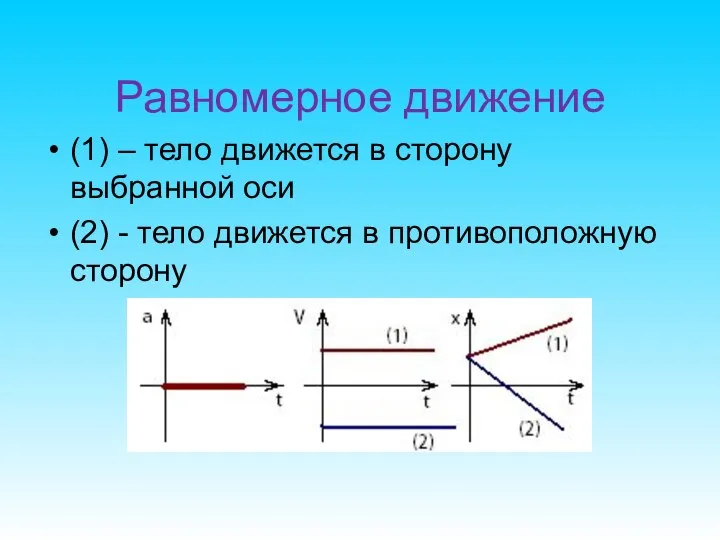
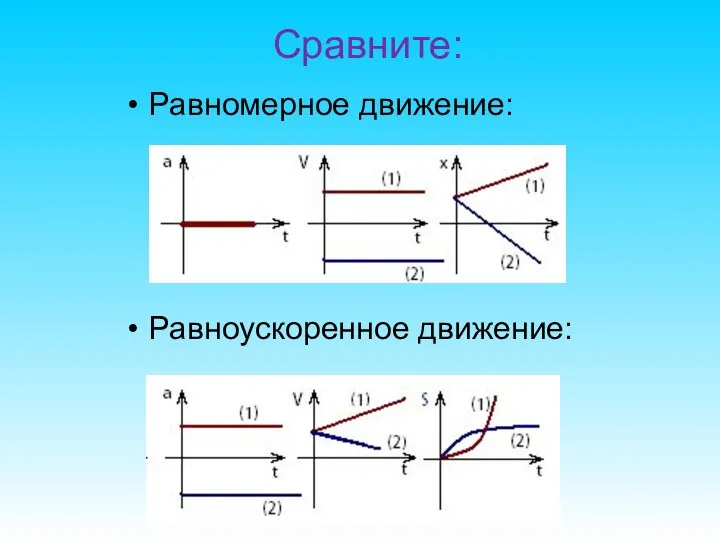
- 32. Равномерное движение (1) – тело движется в сторону выбранной оси (2) - тело движется в противоположную
- 33. Площадь фигуры, заштрихованная под графиком скорости численно равна перемещению за время t Это правило применимо и
- 34. КИНЕМАТИКА Чтобы количественно охарактеризовать это различие между равномерными движениями, водят физическую величину – скорость движения. Скоростью
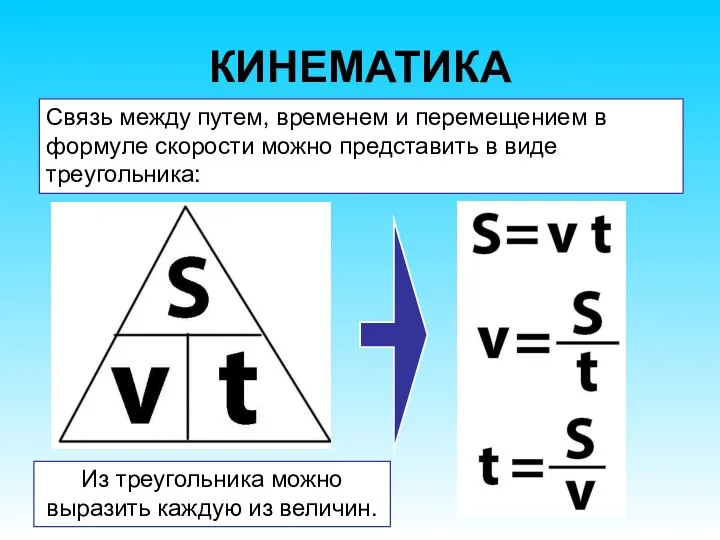
- 35. КИНЕМАТИКА Связь между путем, временем и перемещением в формуле скорости можно представить в виде треугольника: Из
- 36. Основные свойства скорости Скорость величина векторная, то есть она имеет направление (вектор скорости совпадает по направлению
- 37. КИНЕМАТИКА При равномерном прямолинейном движении: Ускорение: Скорость: Перемещение: Пройденный путь: Координата:
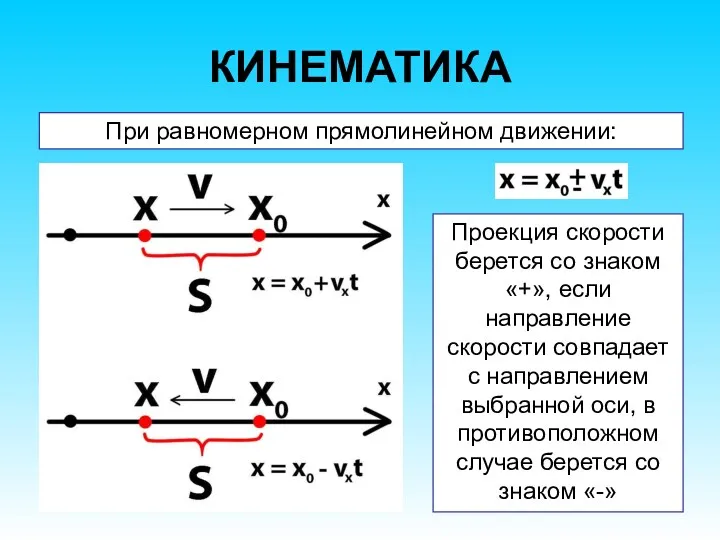
- 38. КИНЕМАТИКА При равномерном прямолинейном движении: Проекция скорости берется со знаком «+», если направление скорости совпадает с
- 39. КИНЕМАТИКА НЕРАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ: - движение, при котором тело за любые равные промежутки времени совершает неодинаковые
- 40. КИНЕМАТИКА РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ - движение, при котором модуль скорости за любые равные промежутки времени изменяется
- 41. КИНЕМАТИКА РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
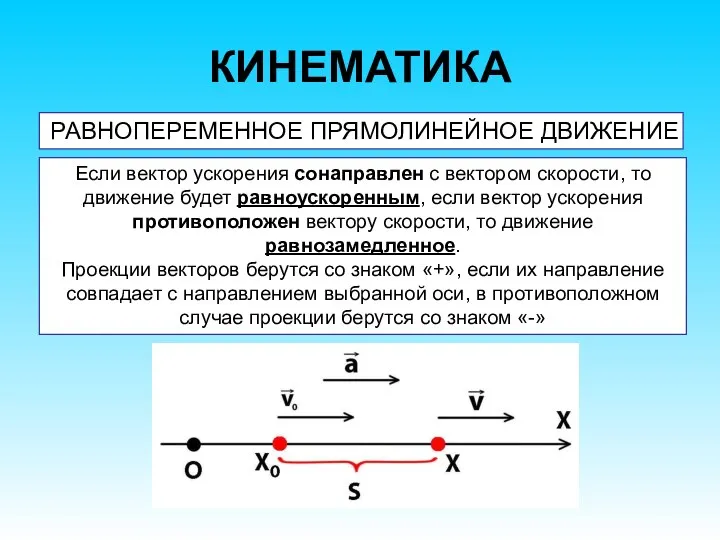
- 42. КИНЕМАТИКА РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ Если вектор ускорения сонаправлен с вектором скорости, то движение будет равноускоренным, если
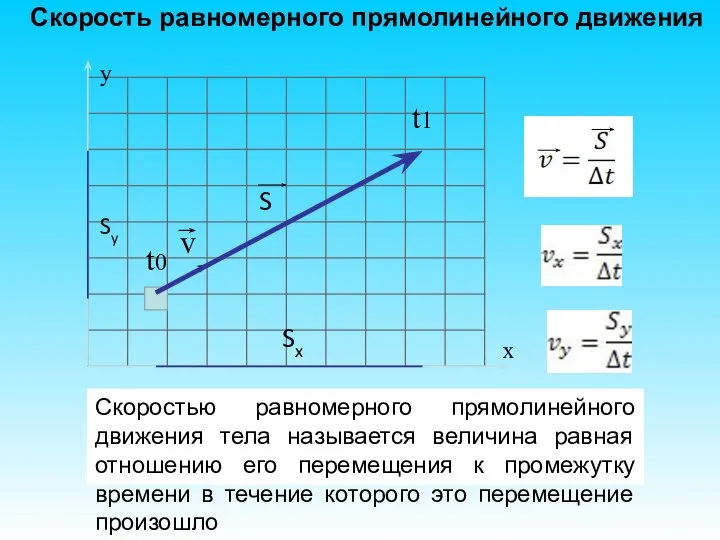
- 43. Скорость равномерного прямолинейного движения t0 t1 x y Скоростью равномерного прямолинейного движения тела называется величина равная
- 45. Основные свойства скорости Скорость величина векторная, то есть она имеет направление (вектор скорости совпадает по направлению
- 46. скорость неравномерного движения: скорость равномерного движения – Направление скорости при: прямолинейном движении – неизменно криволинейном движении
- 47. Ускорение - величина, характеризующая изменение скорости при неравномерном движении тела. Средним ускорением неравномерного движения в интервале
- 48. Неравномерное движение Средняя скорость Мгновенная скорость Физический смысл производной: Производная перемещения (координаты) – есть скорость. S´=V,
- 49. Равноускоренное движение Движение, когда за любые равные промежутки времени скорость тела изменяется одинаково. Это движение с
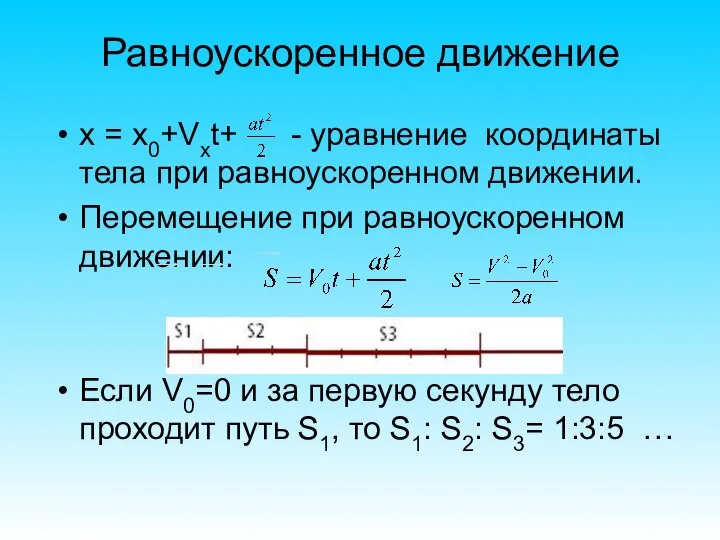
- 50. х = х0+Vхt+ - уравнение координаты тела при равноускоренном движении. Перемещение при равноускоренном движении: Если V0=0
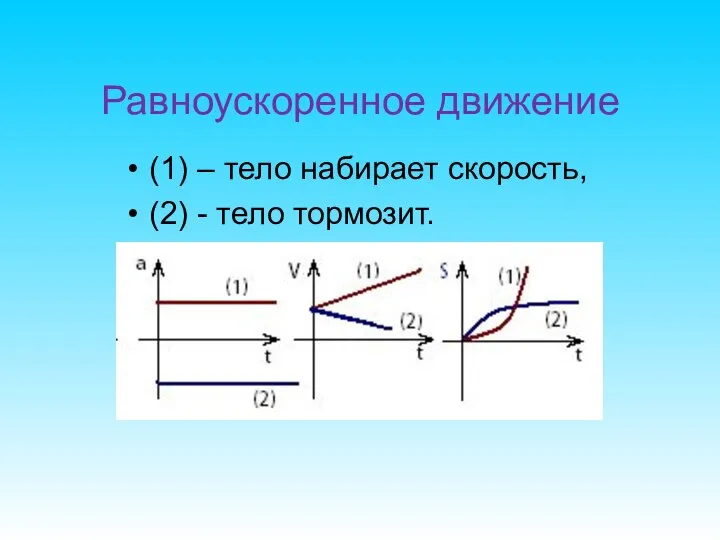
- 51. (1) – тело набирает скорость, (2) - тело тормозит. Равноускоренное движение
- 52. Сравните: Равномерное движение: Равноускоренное движение:
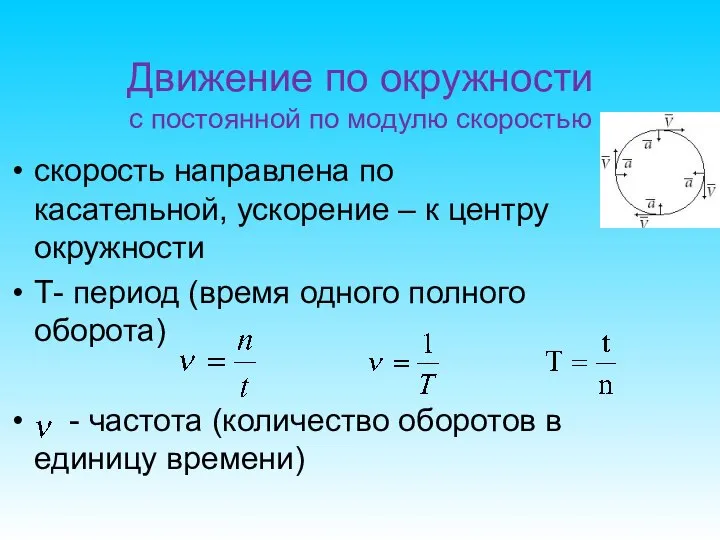
- 53. Движение по окружности с постоянной по модулю скоростью скорость направлена по касательной, ускорение – к центру
- 54. Длина окружности Скорость при движении по окружности - угловая скорость, показывает, на какой угол поворачивается тело
- 55. Ускорение Движение по окружности с постоянной по модулю скоростью
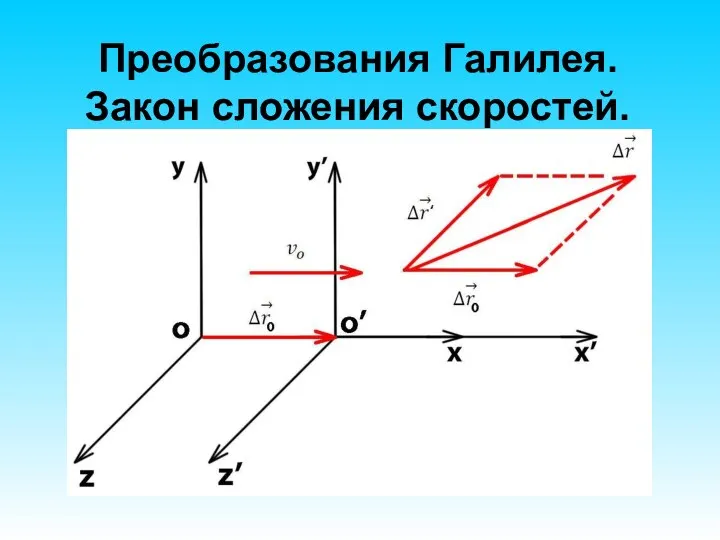
- 57. Преобразования Галилея. Закон сложения скоростей. Позволяют связать между собой координаты некоторой материальной точки в двух разных
- 58. Преобразования Галилея. Закон сложения скоростей.
- 59. Преобразования Галилея. Закон сложения скоростей. Перемещение тела за данный промежуток времени относительно неподвижной системы отсчета равно
- 60. Преобразования Галилея. Закон сложения скоростей. КЛАССИЧЕСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ:
- 61. КИНЕМАТИКА РЕШИТЬ ЗАДАЧУ: 1. Автомобиль прошел первую половину пути со скоростью 10 м/с, а вторую половину
- 62. Кинематика твердого тела Простейшие движения твердого тела Поступательное движение Вращение вокруг неподвижной оси (вращательное)
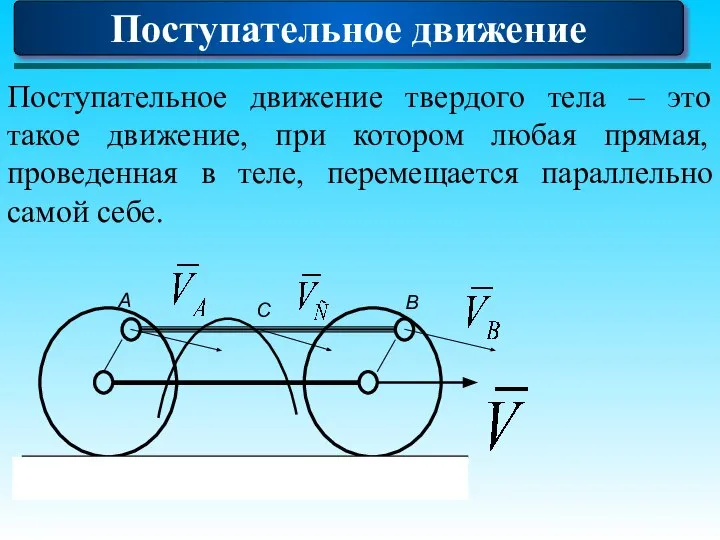
- 63. Поступательное движение твердого тела – это такое движение, при котором любая прямая, проведенная в теле, перемещается
- 64. При поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые
- 65. Вращательное движение твердого тела Вращательное движение твердого тела – это такое движение, при котором две точки
- 66. Положение тела при вращательном движении однозначно определяется углом поворота φ Закон вращательного движения: Вращательное движение
- 67. Z Основные кинематические характеристики вращательного движения: Угловая скорость ω [рад/c] Угловое ускорение ε [рад/c2] Вращательное движение
- 68. Вектор угловой скорости лежит на оси вращения и направлен в сторону, откуда видно, что тело вращается
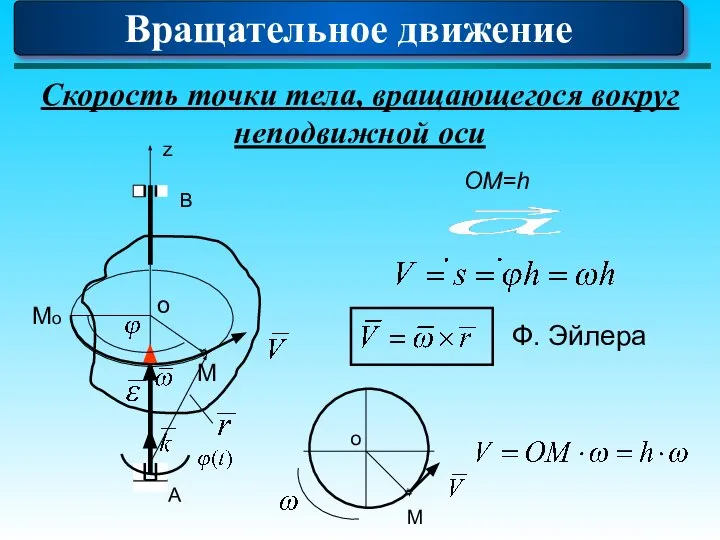
- 69. Скорость точки тела, вращающегося вокруг неподвижной оси A B z Мо М о ОМ=h Ф. Эйлера
- 70. Ускорение точки тела, вращающегося вокруг неподвижной оси М О R Вращательное движение
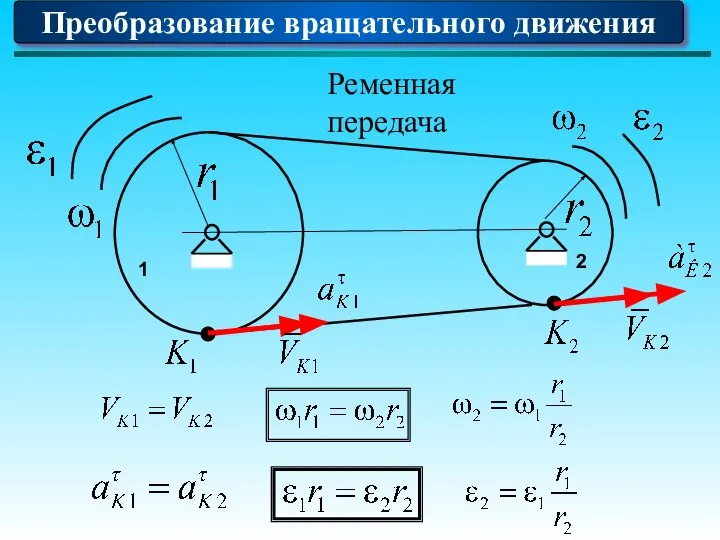
- 71. 1 2 Преобразование вращательного движения Ременная передача
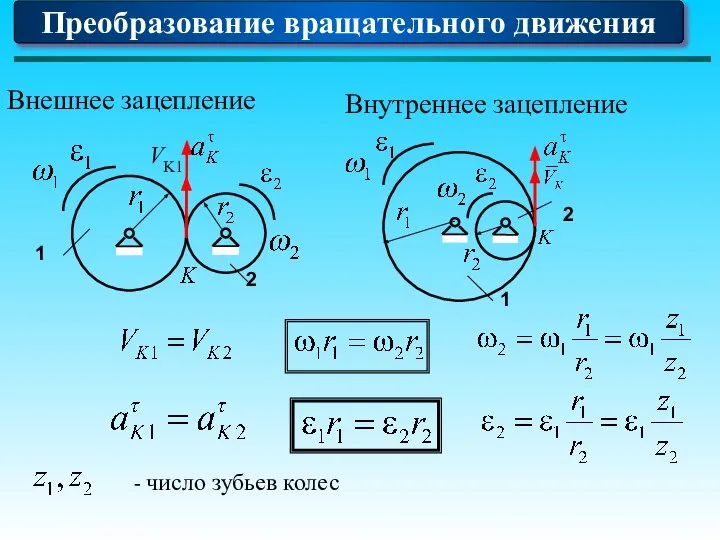
- 72. Внутреннее зацепление Внешнее зацепление 1 2 1 2 - число зубьев колес Преобразование вращательного движения VK1
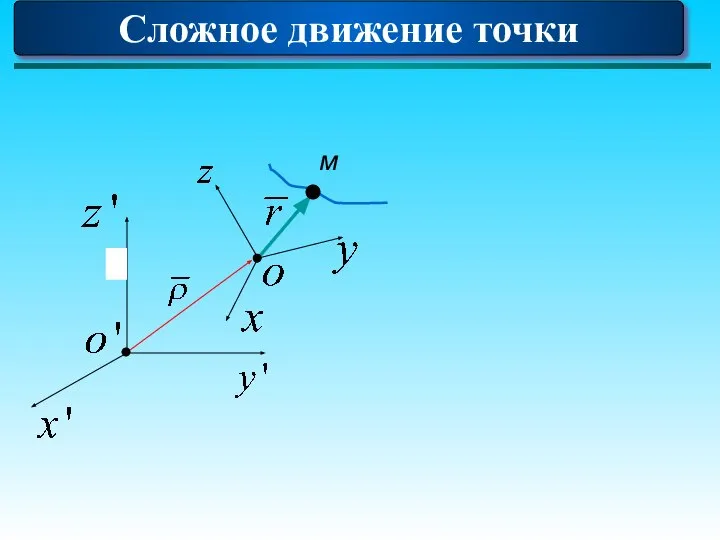
- 73. Сложное движение точки Сложное движение точки Сложное движение точки - такое движение, которое может быть составлено
- 74. Сложное движение точки м
- 75. Сложное движение точки Движение точки относительно основной (неподвижной) системы отсчета называется абсолютным. Движение точки относительно подвижной
- 76. Сложное движение точки Абсолютная скорость точки - скорость относительно неподвижной системы отсчета. Относительная скорость точки -
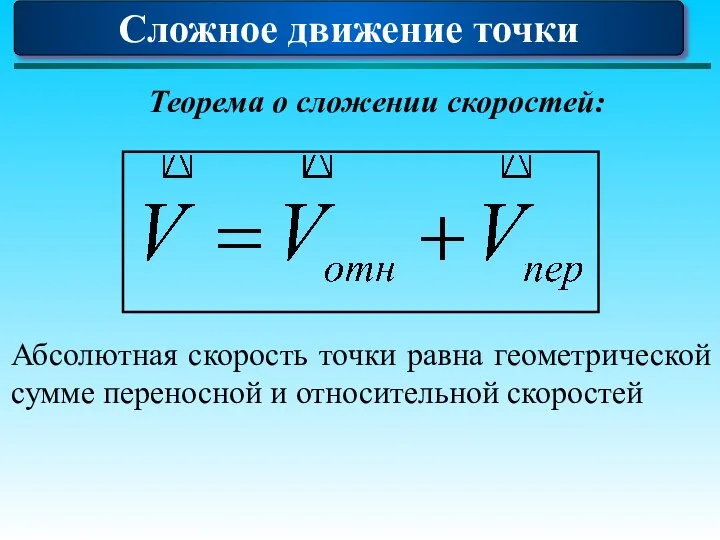
- 77. Сложное движение точки Теорема о сложении скоростей: Абсолютная скорость точки равна геометрической сумме переносной и относительной
- 78. Сложное движение точки - абсолютные - относительные - переносные Скорости и ускорения при сложном движении обозначаются
- 79. Сложное движение точки Теорема Кориолиса Абсолютное ускорение точки равно геометрической сумме переносного ускорения, относительного ускорения и
- 80. Сложное движение точки Ускорение Кориолиса характеризует изменение относительной скорости точки в переносном движении и переносной скорости
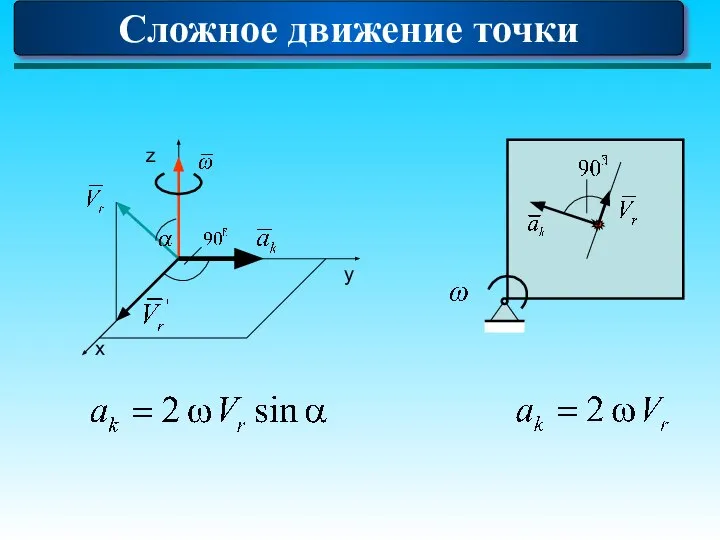
- 81. Сложное движение точки В численном виде, ускорение кориолиса равно Правило Н. Е. Жуковского Чтобы найти направление
- 82. Сложное движение точки x y z
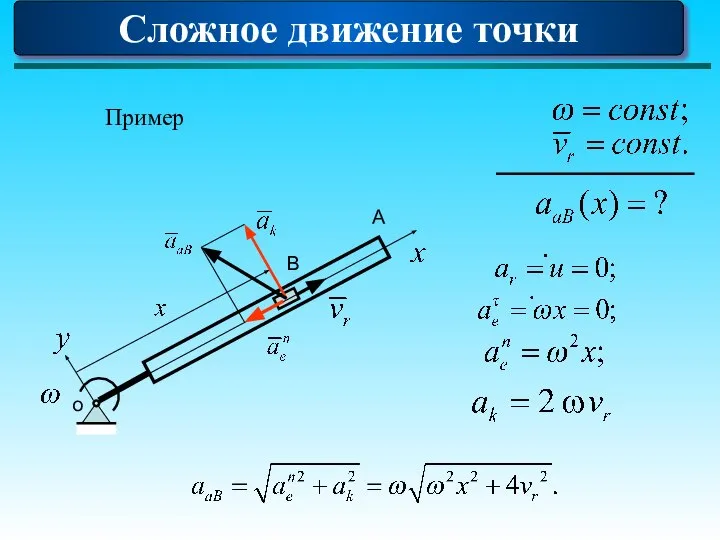
- 83. Сложное движение точки о А В Пример
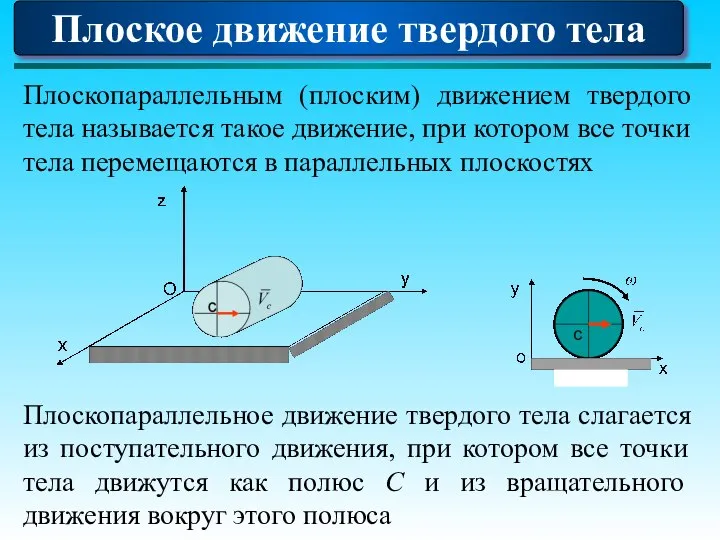
- 84. Плоское движение твердого тела Плоскопараллельным (плоским) движением твердого тела называется такое движение, при котором все точки
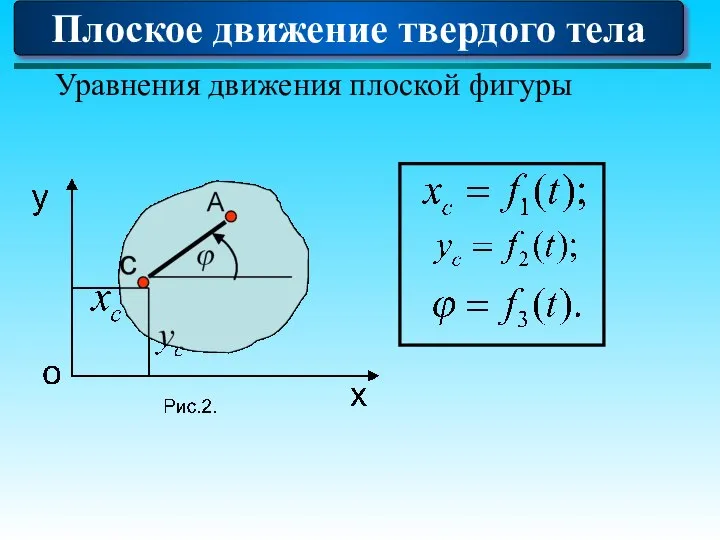
- 85. Плоское движение твердого тела Уравнения движения плоской фигуры
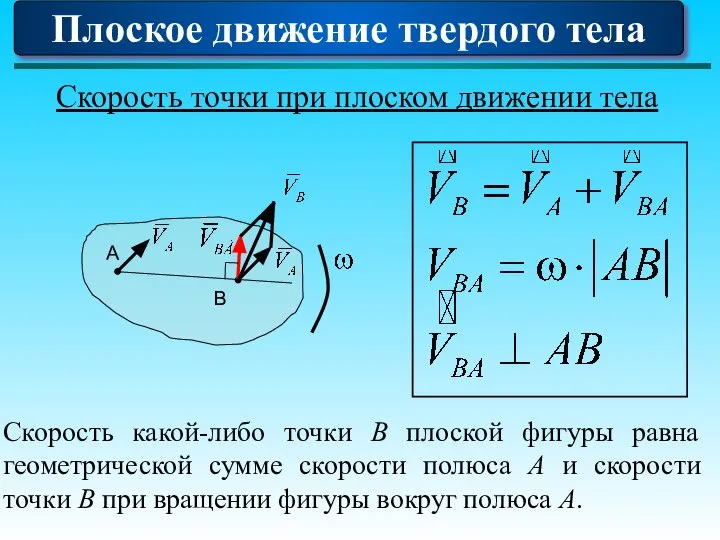
- 86. Плоское движение твердого тела Скорость точки при плоском движении тела Скорость какой-либо точки В плоской фигуры
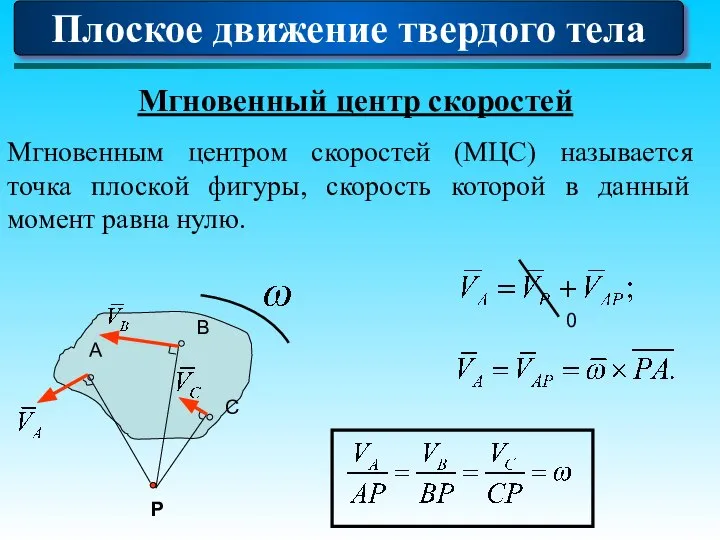
- 87. Плоское движение твердого тела Мгновенный центр скоростей Мгновенным центром скоростей (МЦС) называется точка плоской фигуры, скорость
- 88. Плоское движение твердого тела Свойства МЦС: Скорости всех точек фигуры перпендикулярны отрезкам, соединяющим эти точки с
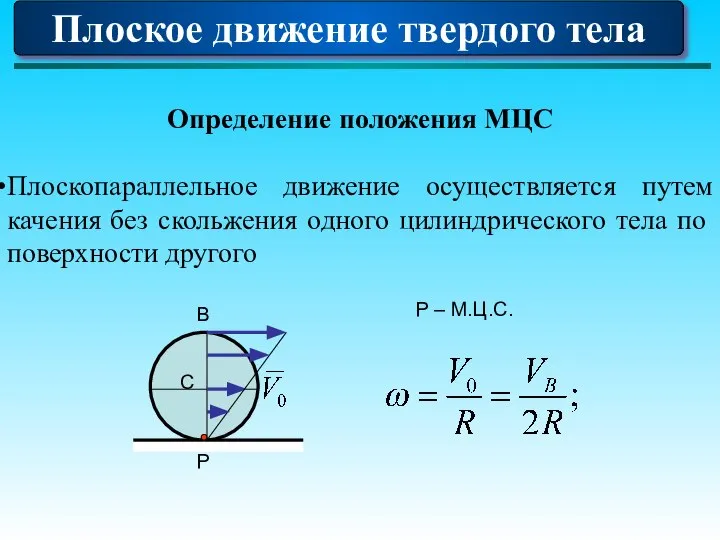
- 89. Плоское движение твердого тела Определение положения МЦС Плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического
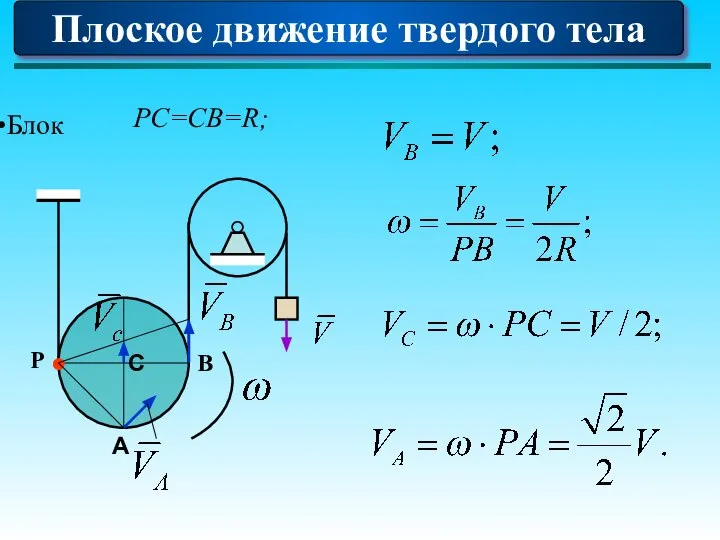
- 90. Плоское движение твердого тела Блок С P A B PC=CB=R;
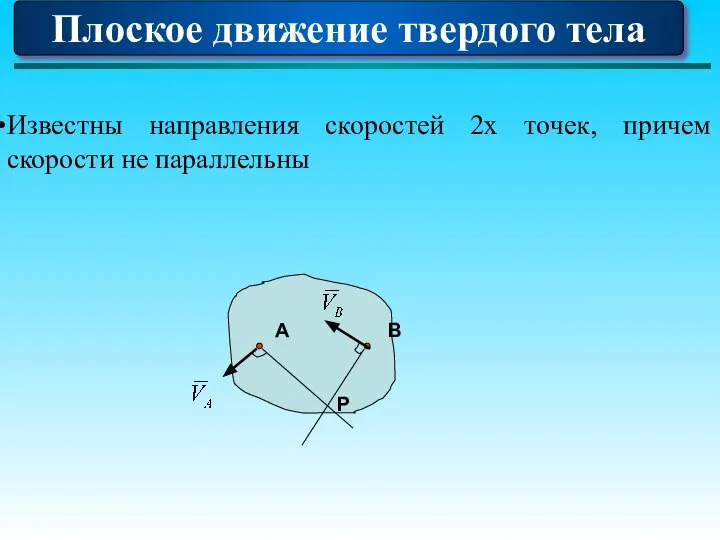
- 91. Плоское движение твердого тела Известны направления скоростей 2х точек, причем скорости не параллельны А В Р
- 93. Скачать презентацию





































![Z Основные кинематические характеристики вращательного движения: Угловая скорость ω [рад/c] Угловое ускорение ε [рад/c2] Вращательное движение](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/976817/slide-66.jpg)










 Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки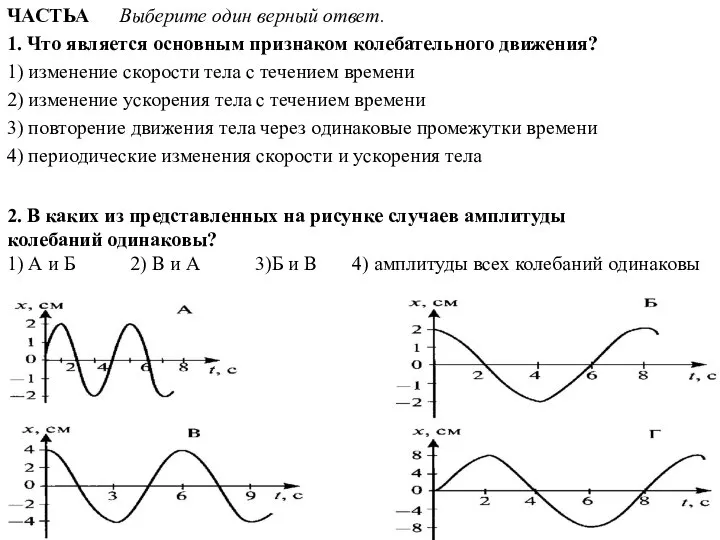 Колебательное движение (9 класс)
Колебательное движение (9 класс) Юные астрофизики
Юные астрофизики АЭС_1663630896
АЭС_1663630896 Удивительный транспорт
Удивительный транспорт Опыты с водой: сильный газ и остуди пар
Опыты с водой: сильный газ и остуди пар Физика – это наука понимать природу…
Физика – это наука понимать природу… Виды соединения проводников. Работа тока
Виды соединения проводников. Работа тока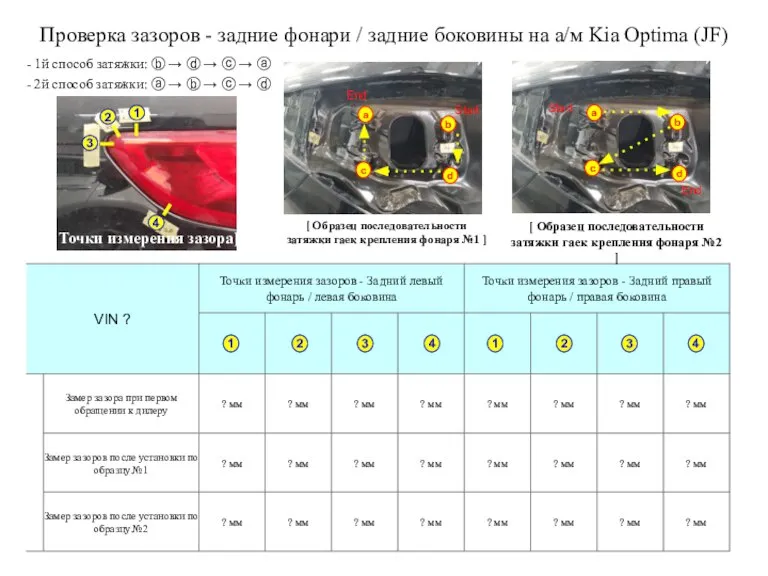 Проверка зазоров - задние фонари / задние боковины на а/м Kia Optima (JF)
Проверка зазоров - задние фонари / задние боковины на а/м Kia Optima (JF) Презентация на тему Вклад отечественной физики в Великую Победу
Презентация на тему Вклад отечественной физики в Великую Победу  Механические передачи и их применение
Механические передачи и их применение Определение высоты отскока шарика для настольного тенниса. Превращение и сохранение энергии. 7 класс
Определение высоты отскока шарика для настольного тенниса. Превращение и сохранение энергии. 7 класс Энтропия и развитие Вселенной
Энтропия и развитие Вселенной Давление твердых тел
Давление твердых тел Световые явления. 8 класс
Световые явления. 8 класс Электростатическое поле в диэлектрике. Лекция 3-2020
Электростатическое поле в диэлектрике. Лекция 3-2020 Модельный ряд двигателей ЗМЗ
Модельный ряд двигателей ЗМЗ Закон всемирного тяготения
Закон всемирного тяготения Стихотворение Ученье - свет, а не ученье - тьма
Стихотворение Ученье - свет, а не ученье - тьма Экспериментальные методы исследования частиц
Экспериментальные методы исследования частиц Путешествие в мир силы тяжести
Путешествие в мир силы тяжести L2_1_Mekhanicheskie_kharakteristiki_metallov
L2_1_Mekhanicheskie_kharakteristiki_metallov Оборудование понизительных подстанций
Оборудование понизительных подстанций Презентация на тему Радиоактивные превращения атомных ядер (9 класс)
Презентация на тему Радиоактивные превращения атомных ядер (9 класс)  Радиация
Радиация Определение скорости движения условной лодки по силе сопротивления при работе на тренажере
Определение скорости движения условной лодки по силе сопротивления при работе на тренажере Продукты питания в руках физикаa
Продукты питания в руках физикаa Формирование атома
Формирование атома