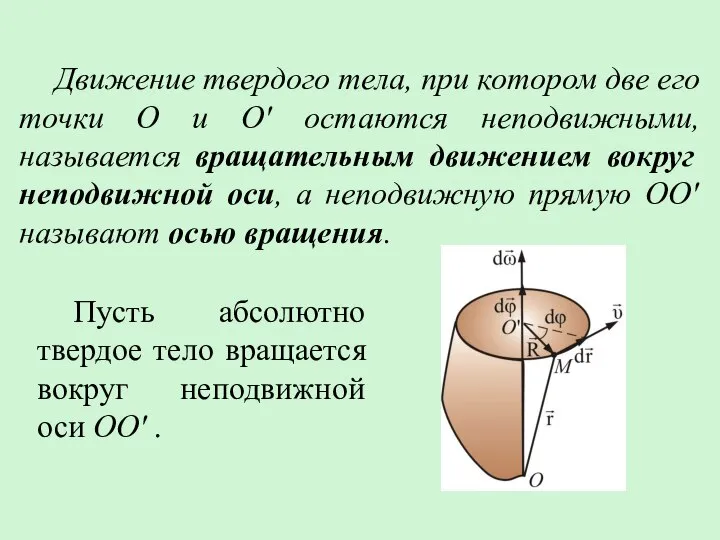
Lect_2

Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения.
Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО' .

Угол поворота характеризует перемещения всего тела за время dt.
Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами.
Эти векторы не имеют определённых точек приложения: они могут откладываться из любой точки оси вращения.
Удобно ввести – вектор элементарного поворота тела, численно равный углу поворота и направленный вдоль оси вращения ОО' так, чтобы глядя вдоль вектора мы видели вращение по часовой стрелке.

Элементарные повороты удовлетворяют обычному правилу сложения векторов:
Угловой скоростью называется вектор численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении ( и всегда
направлены в одну сторону).

Пусть – линейная скорость точки М. За промежуток времени dt точка М проходит путь
В то же время
(центральный угол). Тогда,
или в векторной форме

Вектор ортогонален к векторам и
и направлен в ту же сторону, что и векторное произведение .
Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на угол ).
Частота ν – число оборотов тела за 1 секунду.

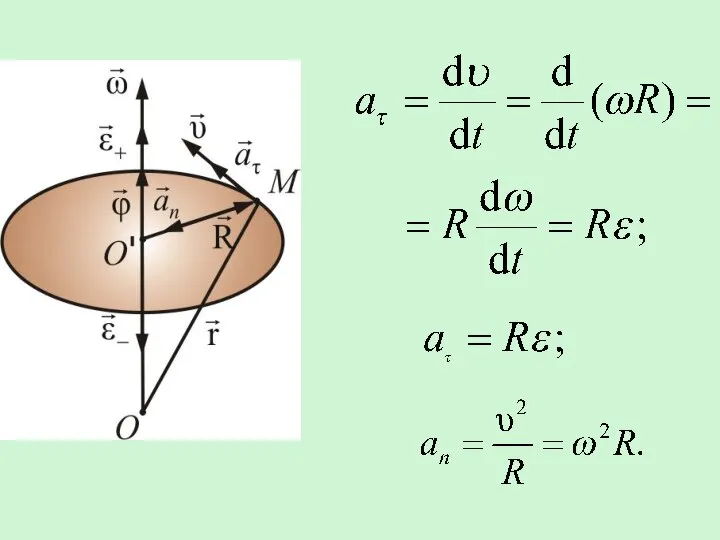
При вращении с угловой скоростью ω, имеем:
Для характеристики неравномерного вращения тел введем вектор углового ускорения :

Вектор направлен в ту же сторону, что и при ускоренном вращении ,
и направлен в противоположную сторону при замедленном вращении .
Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорения точки М через угловую скорость и угловое ускорение:

Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота) направлены вдоль оси вращения.