Содержание
- 2. Вейвлет-преобразование. Позволяет получить частотно-временное представление сигнала и много всякой другой фигни.
- 3. Обработка экспериментальных данных. Вейвлет-преобразование дает наиболее наглядную и информативную картину результатов эксперимента, позволяет очистить исходные данные
- 4. Обработка изображений. Используя вейвлет-преобразование, мы можем сгладить или выделить некоторые детали изображения, выделить важные детали и
- 5. Сжатие данных Для достаточно гладких данных полученные в результате преобразования детали в основном близки по величине
- 6. Нейросети и другие механизмы анализа данных. Вейвлеты представляются весьма удобным и перспективным механизмом очистки и предварительной
- 7. Системы передачи данных и цифровой обработки сигналов. Характерные особенности поведения вейвлет-преобразования в частотно-временной области позволяют существенно
- 8. Преобразование Фурье(ПФ) Это преобразование позволяет получить амплитуду от частоты из амплитуды от времени и наоборот, но
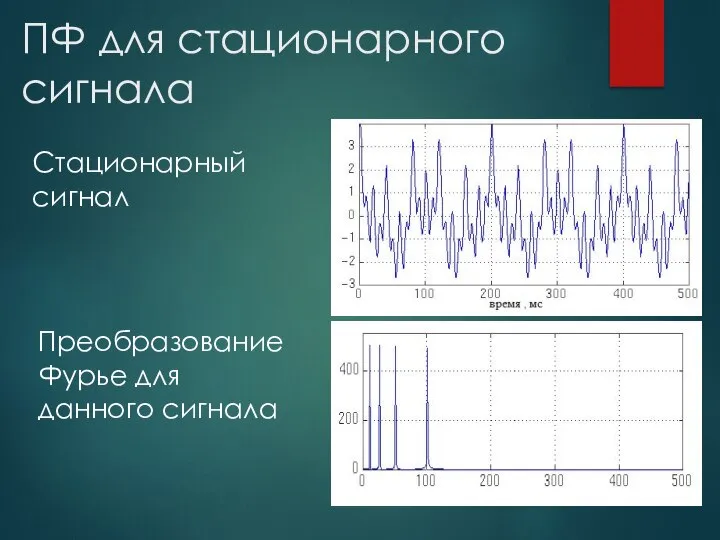
- 9. ПФ для стационарного сигнала Стационарный сигнал Преобразование Фурье для данного сигнала
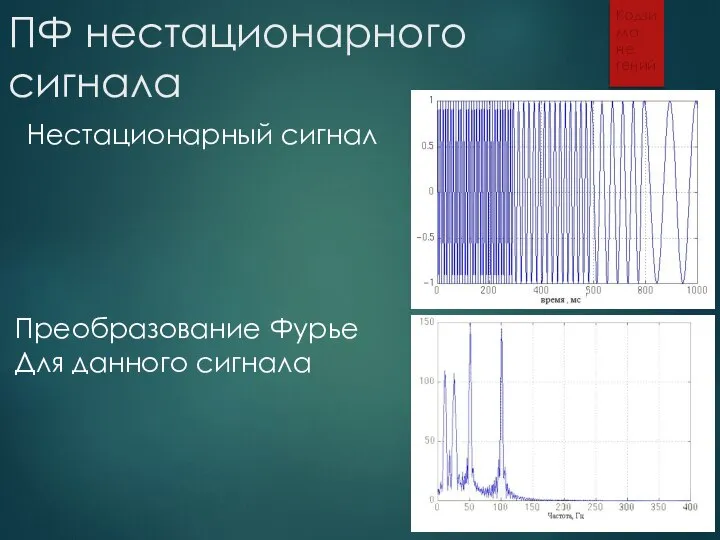
- 10. ПФ нестационарного сигнала Кодзима не гений Нестационарный сигнал Преобразование Фурье Для данного сигнала
- 11. Оконное ПФ(ОПФ) Ранее для нестационарных сигналов использовалось ОПФ. Здесь можно получить и частотно-временное представление сигнала.
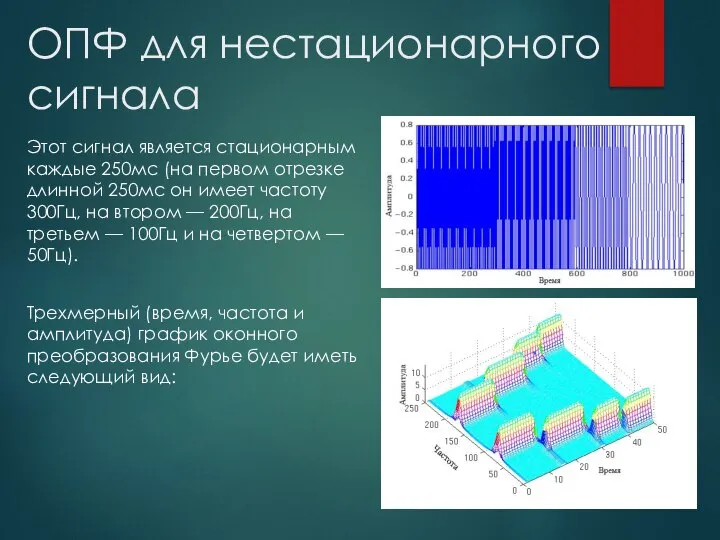
- 12. ОПФ для нестационарного сигнала Этот сигнал является стационарным каждые 250мс (на первом отрезке длинной 250мс он
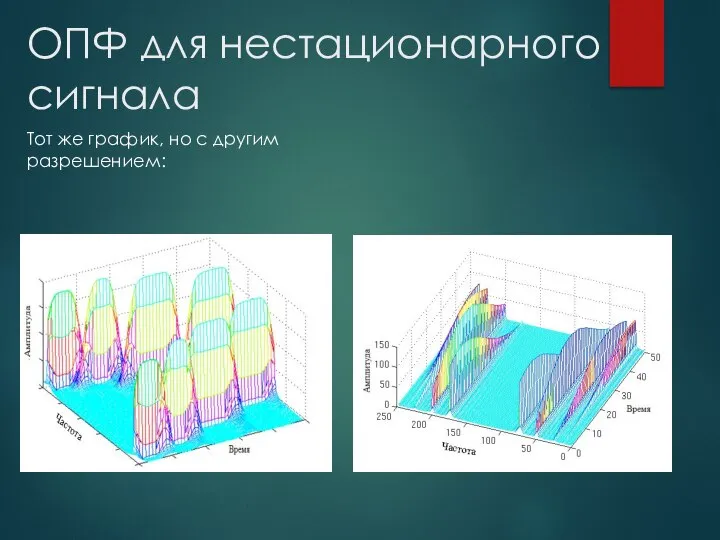
- 13. ОПФ для нестационарного сигнала Тот же график, но с другим разрешением:
- 14. Вейвлет-преобразование. тау - сдвиг, s – масштаб(видно из формулы) пси – материнский вейвлет Материнских вейвлетов используется
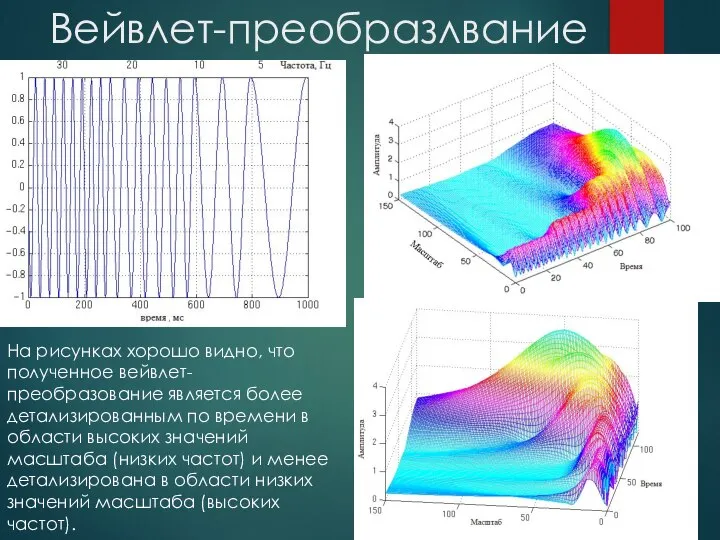
- 15. Вейвлет-преобразлвание На рисунках хорошо видно, что полученное вейвлет-преобразование является более детализированным по времени в области высоких
- 16. Абелевскую премию получил французский математик Ив Мейер за теорию вейвлетов В 1970-х Мейер занимался гармоническим анализом.
- 18. Скачать презентацию










 Определение показателя преломления стекла
Определение показателя преломления стекла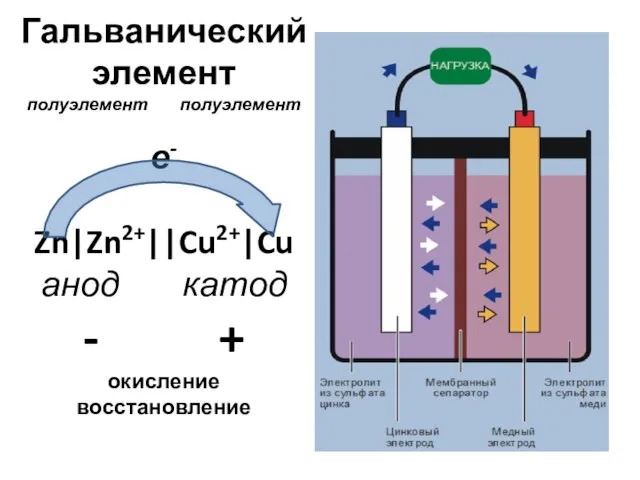 Гальванический элемент, полуэлемент, полуэлемент, е- Zn|Zn2+||Cu2+|Cu, анод, катод, - +, окисление, восстановление
Гальванический элемент, полуэлемент, полуэлемент, е- Zn|Zn2+||Cu2+|Cu, анод, катод, - +, окисление, восстановление Отгадай имя физика. Игра
Отгадай имя физика. Игра Презентация на тему Плавание судов и воздухоплавание
Презентация на тему Плавание судов и воздухоплавание  Разветвленная цепь синусоидального тока
Разветвленная цепь синусоидального тока Упругие волны
Упругие волны Методы исследования частиц
Методы исследования частиц Фізичні властивості металів
Фізичні властивості металів Тормозной путь
Тормозной путь Оптика. Физический диктант
Оптика. Физический диктант Презентация на тему Гелиоцентрическая система Николая Коперника
Презентация на тему Гелиоцентрическая система Николая Коперника  ООО «ФЛЭР ИНЖИНИРИНГ» Профессиональное сварочное оборудование
ООО «ФЛЭР ИНЖИНИРИНГ» Профессиональное сварочное оборудование Механические колебания и волны. Звук
Механические колебания и волны. Звук Константа
Константа Презентация на тему Приливы, отливы, их использование 9 класс
Презентация на тему Приливы, отливы, их использование 9 класс  Теория движения военных колесных машин. Лекция 5
Теория движения военных колесных машин. Лекция 5 Выдающиеся физики
Выдающиеся физики Otáčavé účinky sily
Otáčavé účinky sily Емкость
Емкость Невагомiсть
Невагомiсть Виды дорожной техники
Виды дорожной техники Все под микроскопом
Все под микроскопом Гравитационное взаимодействие
Гравитационное взаимодействие Закон всемирного тяготения
Закон всемирного тяготения Презентация на тему Оптические приборы
Презентация на тему Оптические приборы  Тела, вещества, частицы
Тела, вещества, частицы Презентация на тему Источники звука, звуковые волны и колебания
Презентация на тему Источники звука, звуковые волны и колебания  Что изучает физика (урок 1)
Что изучает физика (урок 1)