Построение изображения в линзах

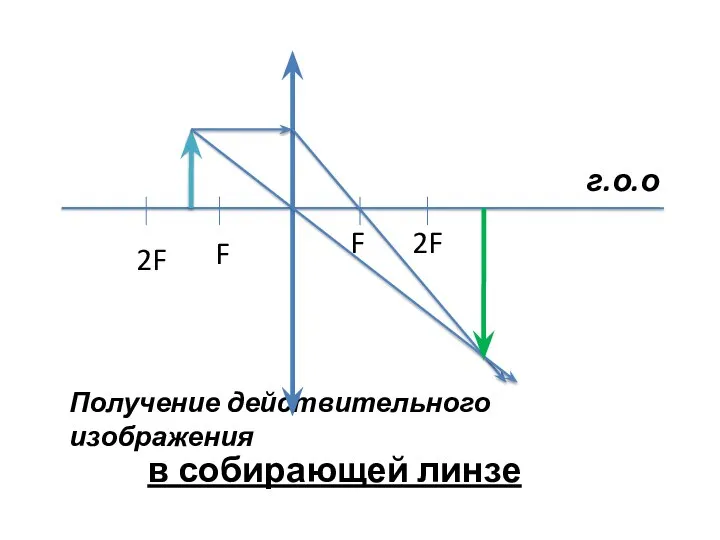
Получение действительного изображения
в собирающей линзе
2F
F
F
2F
г.о.о

Свойства:
Действительное
Перевернутое
увеличенное

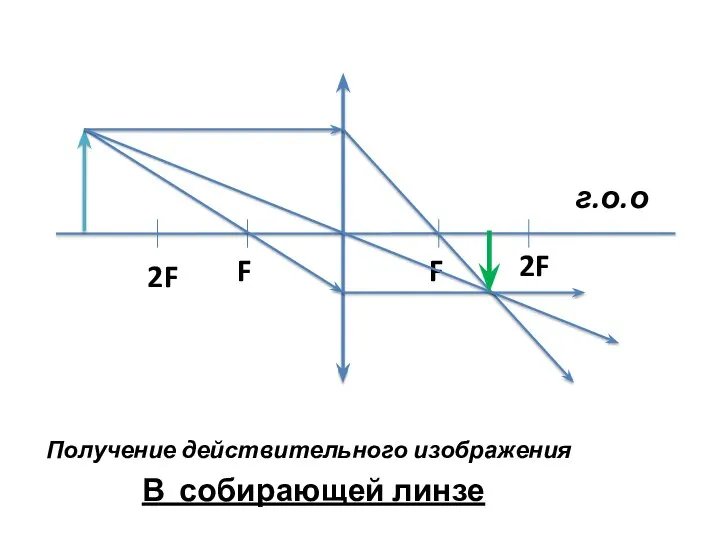
Получение действительного изображения
В собирающей линзе
г.о.о
2F
F
F
2F

Свойства:
Действительное
Перевернутое
уменьшенное

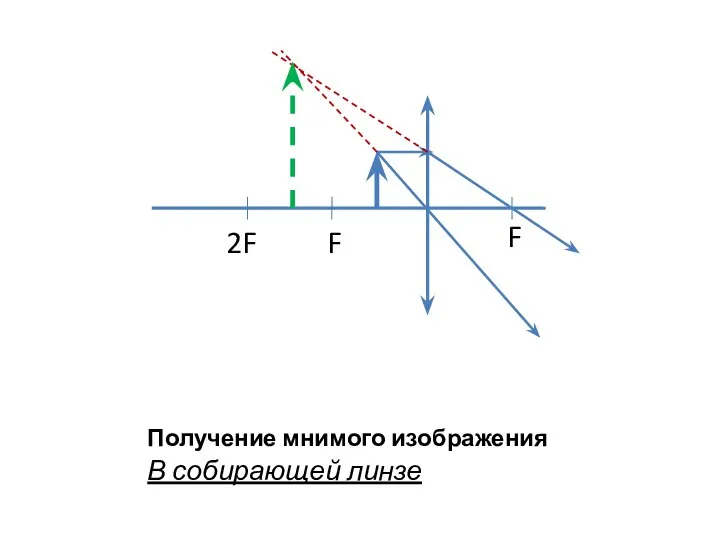
Получение мнимого изображения
В собирающей линзе
F
2F
F

Свойства:
Мнимое
Прямое
увеличенное

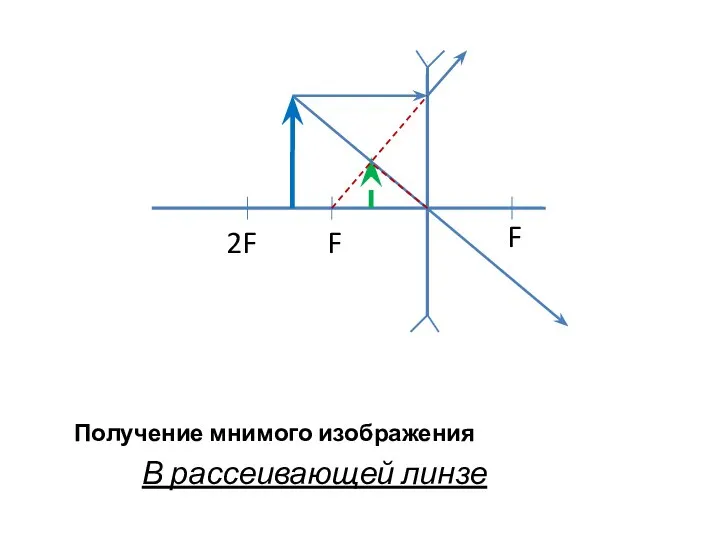
В рассеивающей линзе
Получение мнимого изображения
F
2F
F

Свойства:
Мнимое
Прямое
уменьшенное

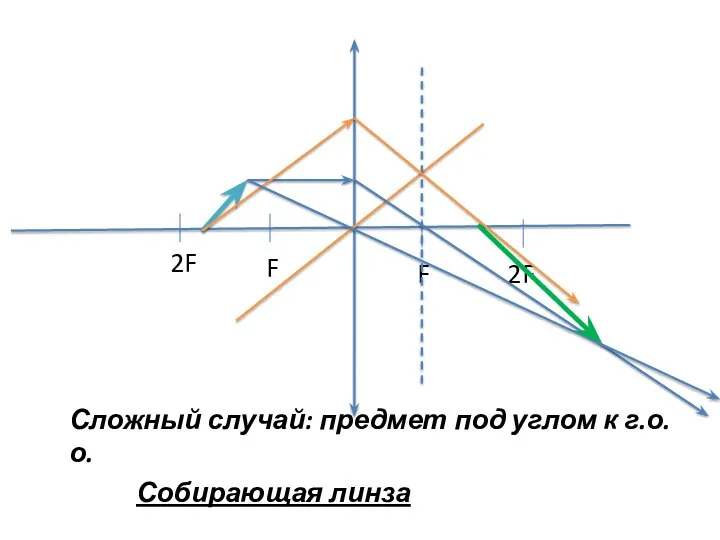
Сложный случай: предмет под углом к г.о.о.
Собирающая линза
2F
F
F
2F

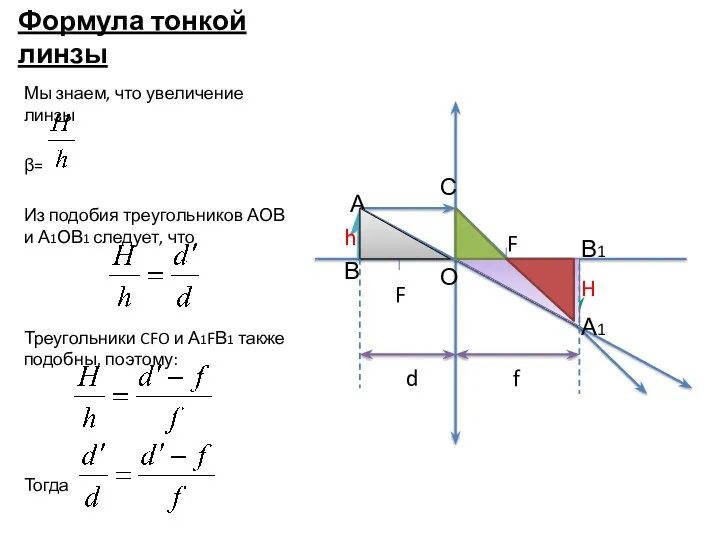
Формула тонкой линзы
Мы знаем, что увеличение линзы
β=
Из подобия треугольников АОВ и А1ОВ1 следует, что
Треугольники CFO и А1FВ1 также подобны, поэтому:
Тогда
F
F
О
В
А
В1
А1
С
h
H
d
f