Колебания и волны. Лекция 3.1

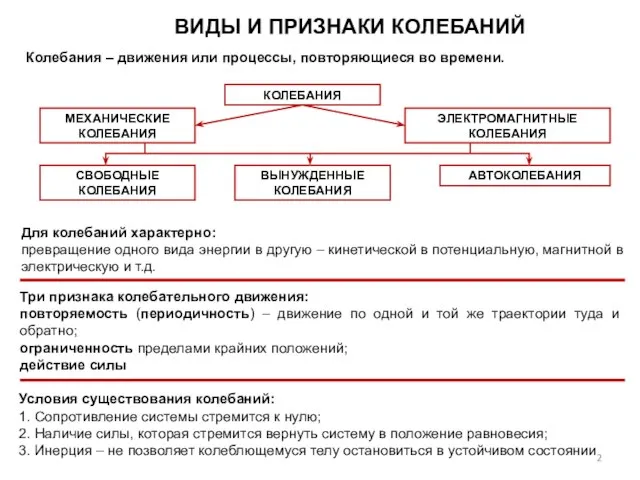
ВИДЫ И ПРИЗНАКИ КОЛЕБАНИЙ
Для колебаний характерно:
превращение одного вида энергии в другую – кинетической в потенциальную, магнитной в электрическую и т.д.
Колебания – движения или процессы, повторяющиеся во времени.
Условия существования колебаний:
1. Сопротивление системы стремится к нулю;
2. Наличие силы, которая стремится вернуть систему в положение равновесия;
3. Инерция – не позволяет колеблющемуся телу остановиться в устойчивом состоянии
Три признака колебательного движения:
повторяемость (периодичность) – движение по одной и той же траектории туда и обратно;
ограниченность пределами крайних положений;
действие силы

КОЛЕБАНИЯ
Свободные (или собственные) колебания – совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему
Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.
Автоколебания — незатухающие колебания, которые могут существовать в системе без воздействия на нее внешних периодических сил
‒ незатухающие колебания в системе, амплитуда и частота которых
в течение длительного промежутка времени могут оставаться постоянными, не зависят от начальных условий и определяются свойствами самой системы

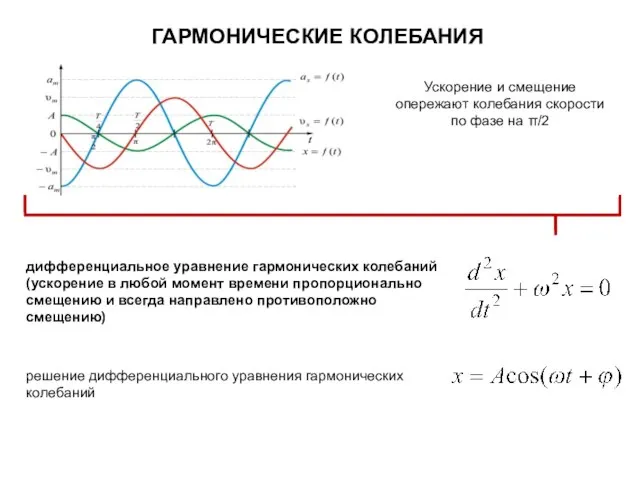
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Уравнение колебательного движения записывают в виде
х – смещение в данный момент времени, расстояние материальной точки от положения равновесия до точки, в которой она находится (м);
А – амплитуда колебания, характеризующая величину наибольшего смещения материальной точки от положения равновесия (м);
(ωt + ϕ0 ) – фаза колебания, определяет смещение колеблющейся величины от положения равновесия в данный момент времени (рад);
– циклическая (круговая, собственная) частота, показывает сколько колебаний совершается за 2π секунд (рад/с);
ϕ0 – начальная фаза колебания, определяет смещение колеблющейся величины от положения равновесия в начальный момент времени (рад)
или
Колебания, которые совершаются с течением времени по закону синуса или косинуса, называют гармоническими колебаниями.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Период колебания Т – это промежуток времени одного полного колебания (с).
Период колебания Т- минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание
Частота колебаний определяется, как число полных колебаний в 1 секунду. Частоту, измеряют в герцах (1/с; Гц):
1 Гц = 1 колебание в секунду.
Циклическая (круговая, собственная) частота – число полных колебаний за 2 π секунд. Измеряют в рад/с.

Амплитуда скорости гармонических
колебаний
Амплитуда ускорения гармонических
колебаний
Скорость гармонических колебаний
Ускорение гармонических колебаний
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Смещение описывается уравнением
Сила при гармонических колебаниях
Амплитуда силы при гармонических
колебаниях
сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
решение дифференциального уравнения гармонических колебаний
Ускорение и смещение опережают колебания скорости по фазе на π/2
дифференциальное уравнение гармонических колебаний (ускорение в любой момент времени пропорционально смещению и всегда направлено противоположно смещению)

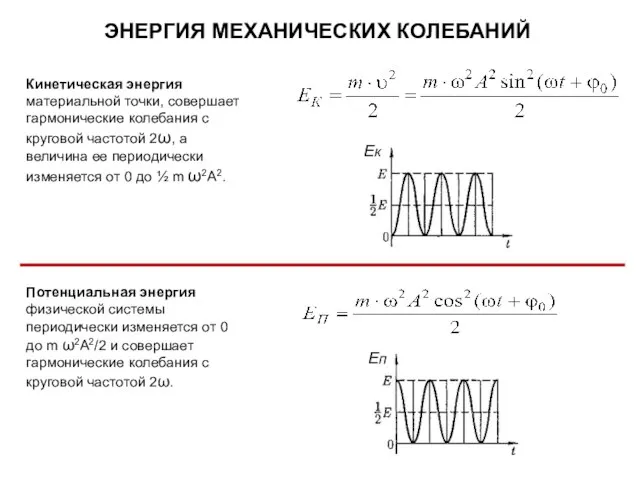
Кинетическая энергия материальной точки, совершает гармонические колебания с круговой частотой 2ω, а величина ее периодически изменяется от 0 до ½ m ω2A2.
ЭНЕРГИЯ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ
Потенциальная энергия физической системы периодически изменяется от 0 до m ω2A2/2 и совершает гармонические колебания с круговой частотой 2ω.

ПОЛНАЯ ЭНЕРГИЯ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ
Полная энергия колебательной системы, совершающей колебания
Амплитуда полной энергии не зависит от времени
Полная механическая энергия системы:
Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения
энергии, поскольку упругая сила консервативна

ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
Гармоническим осциллятором называется система, совершающая колебания, изменяющиеся по гармоническому закону и описываемые уравнением вида
Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур

Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине с жесткостью k, совершающий гармонические колебания под действием упругой силы
ПРУЖИННЫЙ МАЯТНИК
Период колебаний пружинного маятника
Квадрат круговой частоты прямо пропорционален коэффициенту жесткости пружины k и обратно пропорционален его массе m
Выполняется если масса пружины мала по сравнению с массой тела
Потенциальная энергия пружинного маятника

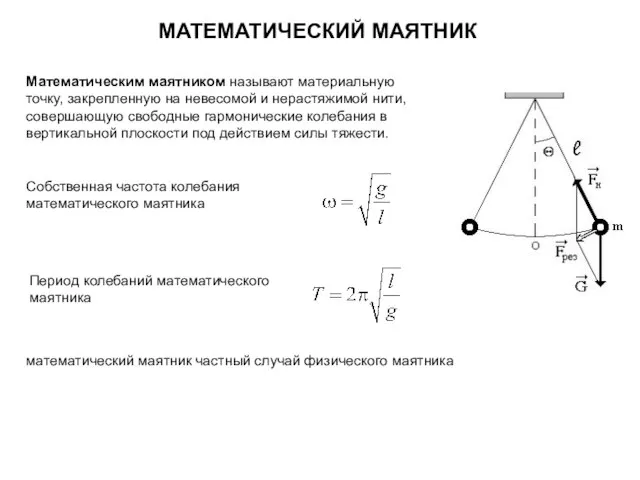
МАТЕМАТИЧЕСКИЙ МАЯТНИК
Математическим маятником называют материальную точку, закрепленную на невесомой и нерастяжимой нити, совершающую свободные гармонические колебания в вертикальной плоскости под действием силы тяжести.
Собственная частота колебания математического маятника
Период колебаний математического маятника
математический маятник частный случай физического маятника

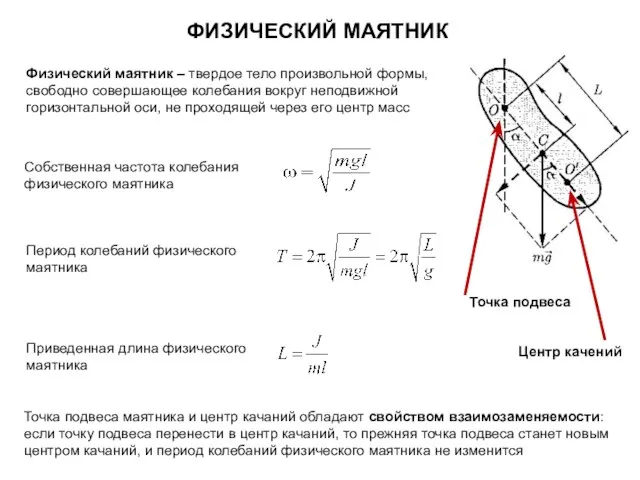
ФИЗИЧЕСКИЙ МАЯТНИК
Физический маятник ‒ твердое тело произвольной формы, свободно совершающее колебания вокруг неподвижной горизонтальной оси, не проходящей через его центр масс
Собственная частота колебания физического маятника
Период колебаний физического маятника
Точка подвеса
Центр качений
Точка подвеса маятника и центр качаний обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка подвеса станет новым центром качаний, и период колебаний физического маятника не изменится
Приведенная длина физического маятника

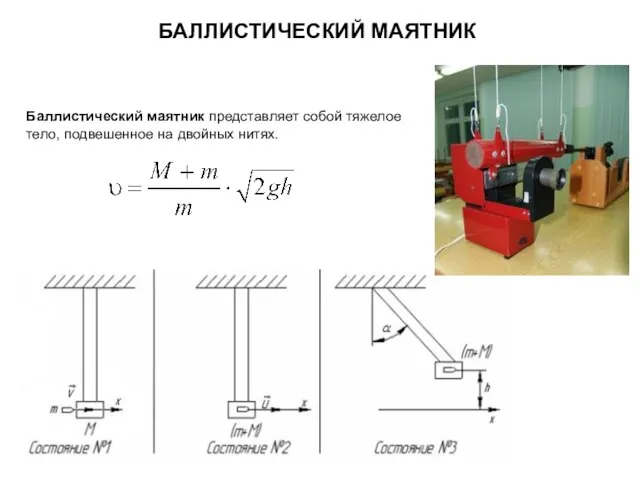
БАЛЛИСТИЧЕСКИЙ МАЯТНИК
Баллистический маятник представляет собой тяжелое тело, подвешенное на двойных нитях.

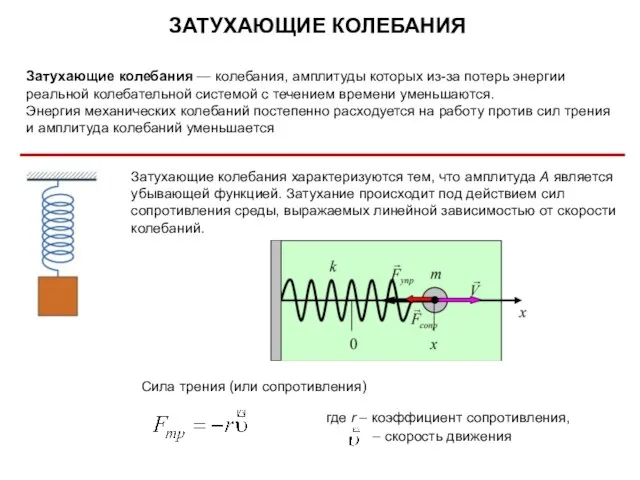
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.
Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний уменьшается
Сила трения (или сопротивления)
где r – коэффициент сопротивления,
Затухающие колебания характеризуются тем, что амплитуда A является убывающей функцией. Затухание происходит под действием сил сопротивления среды, выражаемых линейной зависимостью от скорости колебаний.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Дифференциальное уравнение свободных затухающих колебаний
где х — колеблющаяся величина, описывающая тот или иной физический процесс,
β = const —коэффициент затухания,
ω0 — собственная циклическая частотой колебательной системы, т. е. частота свободных незатухающих колебаний той же колебательной системы при β = 0 (при отсутствии потерь энергии)
Амплитуда свободных затухающих колебаний
Коэффициент затухания
r — коэффициент сопротивления
Собственная частота системы ‒ частота, с которой совершались бы свободные колебания системы в отсутствии сопротивления среды
Уравнение свободных затухающих колебаний

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Дифференциальное уравнение свободных затухающих колебаний
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Апериодичность
Если β > 1, то колебания с самого начала экспоненциально затухают. Сильное затухание
Граница апериодичности
Если β = 1, в данном случае может иметь место временный рост, но потом ‒ экспоненциальное затухание.
Слабое затухание
Если β <1

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Время релаксации ‒ промежуток времени τ = 1/β, в течение которого амплитуда затухающих колебаний уменьшается в е = 2.7 раз
Период затухающих колебаний равен (условно)
Коэффициент затухания ‒ определяет, насколько быстро уменьшается амплитуда колебаний с течением времени.
Ne – число колебаний за промежуток времени, в течение которого амплитуда уменьшается в е раз. Время одного колебания – период
Циклическая частота затухающих колебаний

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Логарифмическим декрементом затухания ‒ отношения амплитуд затухающих колебания в моменты времени, разделенные промежутком в один период
Ne— число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина
Добротность ‒ физическая величина, характеризующая потери энергии при затухающих колебаниях. Добротность безразмерна.

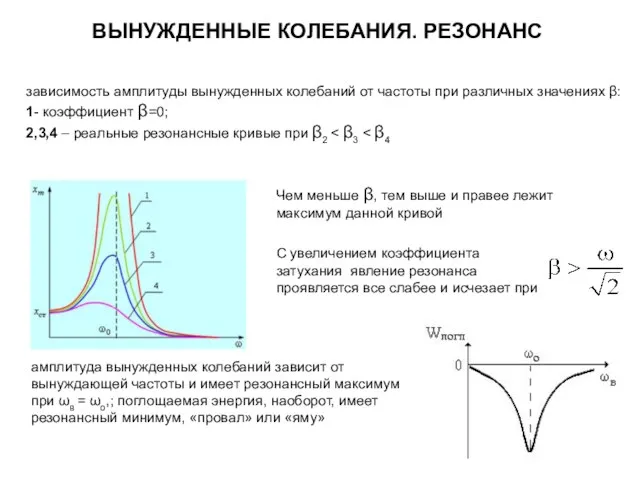
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
зависимость амплитуды вынужденных колебаний от частоты при различных значениях β:
1- коэффициент β=0;
2,3,4 – реальные резонансные кривые при β2 < β3 < β4
Чем меньше β, тем выше и правее лежит максимум данной кривой
амплитуда вынужденных колебаний зависит от вынуждающей частоты и имеет резонансный максимум при ωв = ωo,; поглощаемая энергия, наоборот, имеет резонансный минимум, «провал» или «яму»
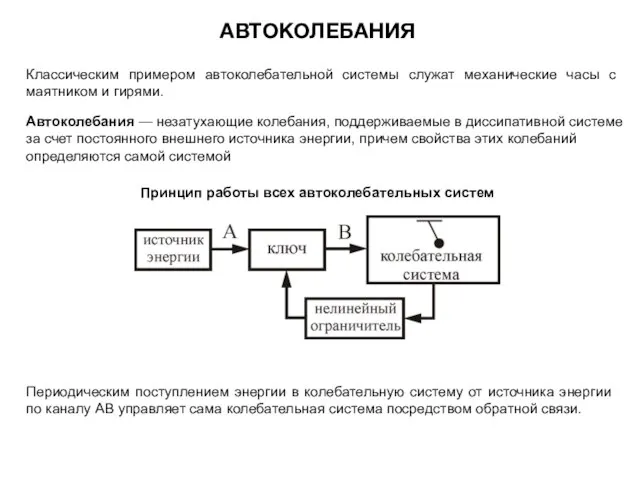
С увеличением коэффициента затухания явление резонанса проявляется все слабее и исчезает при

АВТОКОЛЕБАНИЯ
Принцип работы всех автоколебательных систем
Периодическим поступлением энергии в колебательную систему от источника энергии по каналу АВ управляет сама колебательная система посредством обратной связи.
Классическим примером автоколебательной системы служат механические часы с маятником и гирями.
Автоколебания — незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой

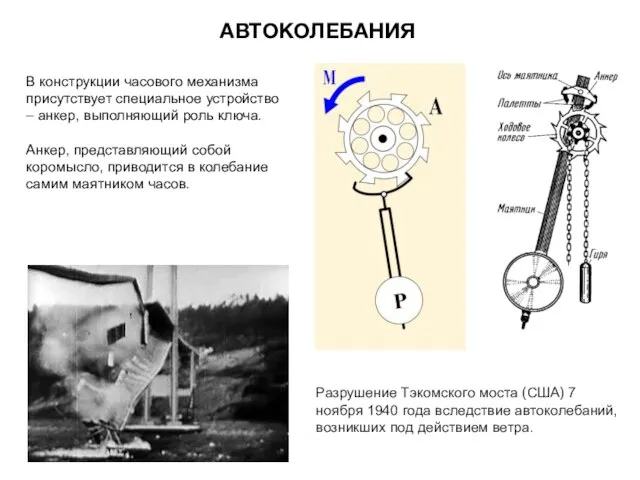
В конструкции часового механизма присутствует специальное устройство – анкер, выполняющий роль ключа.
Анкер, представляющий собой коромысло, приводится в колебание самим маятником часов.
АВТОКОЛЕБАНИЯ
Разрушение Тэкомского моста (США) 7 ноября 1940 года вследствие автоколебаний, возникших под действием ветра.

ЗАДАЧИ 1
1.1 Начальная фаза гармонического колебания ϕ=0. При смещении точки от положения равновесия х1 = 2,4 см скорость точки v1 = 3 см/с, а при смещении x2 = 2,8 см ее скорость v2 = 2 см/с. Найти амплитуду А и период Т этого колебания.
1.2 К пружине подвешен груз массой m = 10 кг. Зная, что пружина под влиянием силы F = 9,8 Н растягивается на l = 1.5 см, найти период Т вертикальных колебаний груза.
1.3 Период затухающих колебаний T=4с; логарифмический декремент затухания λ=1,6; начальная фаза ϕ0=0. При t=T/4 смещение точки x=4,5см. Написать уравнение движения этого колебания.

СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Электромагнитными колебаниями называют периодические взаимосвязанные изменения заряда, силы тока и напряжения.
Свободными колебаниями называют такие, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.
Свободные электромагнитные колебания – это периодически повторяющиеся изменения электромагнитных величин (q – электрический заряд, I – сила тока, U – разность потенциалов), происходящие без потребления энергии от внешних источников.
Простейшей электрической системой, способной совершать свободные колебания, является последовательный LC-контур или колебательный контур.

СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Колебания в контуре можно вызвать либо зарядив конденсатор, либо вызвав в катушке ток
в начальный момент времени t=0 между обкладками конденсатора возникнет электрическое поле, энергия которого
При замыкании конденсатора на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток I.
Энергия электрического поля конденсатора будет уменьшаться, а энергия магнитного поля катушки возрастать
Так как R ≈ 0, то, согласно закону сохранения энергии, полная энергия колебательного контура равна

заряд на обкладке конденсатора изменяется по гармоническому закону с частотой ω0
СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Напряжение на конденсаторе
Сила тока в катушке
ω0 – собственная частота контура
Период колебаний определяется по формуле Томсона

Вынужденные электромагнитные колебания в цепи, содержащей резистор, катушку индуктивности и конденсатор называются переменным током
Переменный ток квазистационарный ‒ мгновенные значения силы тока в сечениях цепи одинаковы, так как их изменения происходят медленно, а электромагнитные возмущения распространяются по цепи со скоростью света
Закон Ома для контура
Волновое сопротивление [Ом]
Законы Ома и правила Кирхгофа (установлены для постоянного тока) − справедливы для мгновенных значений изменяющегося тока
Электромагнитные сигналы распространяются по цепи со скоростью света с, l – длина электрической цепи; t - время распространения сигнала в данной цепи
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Реальный контур обладает активным сопротивлением R. Энергия контура расходуется в на нагревание и колебания затухают
ВЫНУЖДЕННЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Уравнение свободных затухающих колебаний в контуре R,L и C
Решение уравнения:
Коэффициент затухания
Логарифмический декремент затухания
Декремент затухания
Вынужденными называются колебания в цепи под действием внешней периодической электродвижущей силы

К контуру подается переменное напряжение U :
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Уравнение силы тока
Уравнение заряда

ЗАКОН ОМА ДЛЯ ПЕРЕМЕННОГО ТОКА
Напряжение в цепи
Закон Ома для переменного тока с
последовательно соединенными R, L и C
полное сопротивление цепи или импеданс - отвечает за потерю мощности в цепи
угол ϕ определяет разность фаз между напряжением и силой тока
реактивное сопротивление - определяет величину энергии пульсирующей в цепи с частотой 2ω

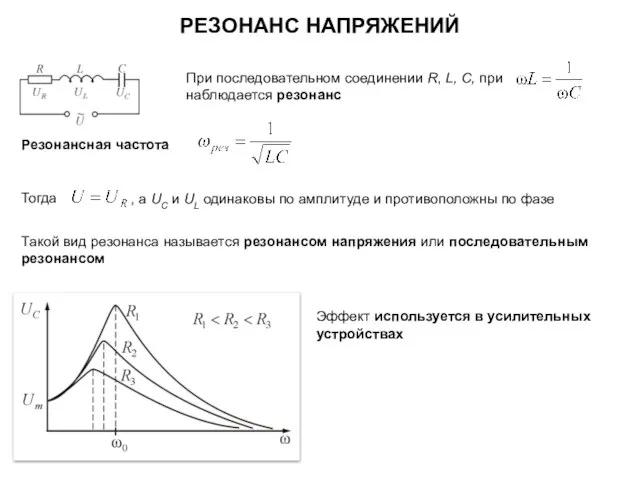
При последовательном соединении R, L, С, при наблюдается резонанс
, а UC и UL одинаковы по амплитуде и противоположны по фазе
Тогда
Такой вид резонанса называется резонансом напряжения или последовательным резонансом
РЕЗОНАНС НАПРЯЖЕНИЙ
Резонансная частота
Эффект используется в усилительных устройствах

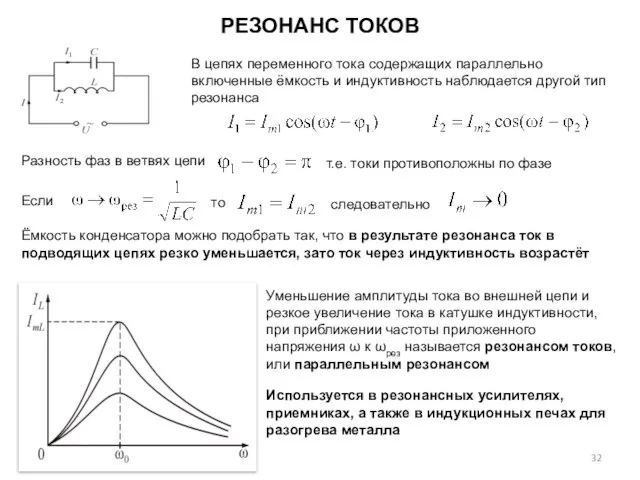
РЕЗОНАНС ТОКОВ
В цепях переменного тока содержащих параллельно включенные ёмкость и индуктивность наблюдается другой тип резонанса
Разность фаз в ветвях цепи
т.е. токи противоположны по фазе
Если
то
следовательно
Ёмкость конденсатора можно подобрать так, что в результате резонанса ток в подводящих цепях резко уменьшается, зато ток через индуктивность возрастёт
Уменьшение амплитуды тока во внешней цепи и резкое увеличение тока в катушке индуктивности, при приближении частоты приложенного напряжения ω к ωрез называется резонансом токов, или параллельным резонансом
Используется в резонансных усилителях, приемниках, а также в индукционных печах для разогрева металла

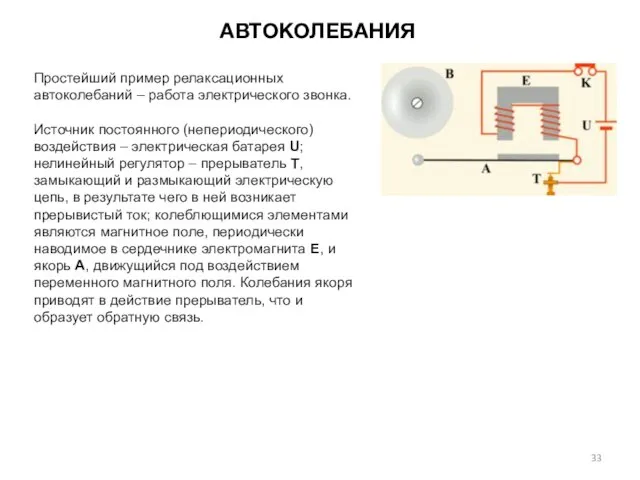
АВТОКОЛЕБАНИЯ
Простейший пример релаксационных автоколебаний – работа электрического звонка.
Источник постоянного (непериодического) воздействия – электрическая батарея U; нелинейный регулятор – прерыватель T, замыкающий и размыкающий электрическую цепь, в результате чего в ней возникает прерывистый ток; колеблющимися элементами являются магнитное поле, периодически наводимое в сердечнике электромагнита E, и якорь A, движущийся под воздействием переменного магнитного поля. Колебания якоря приводят в действие прерыватель, что и образует обратную связь.

ВОЛНЫ. КЛАССИФИКАЦИЯ ВОЛН
Волна – это процесс распространения колебаний (возмущений) в среде
Волнами называют распространяющиеся в веществе или поле возмущения какой-либо физической величины, характеризующей состояния этого вещества или поля.
Если какое-либо тело (источник колебаний) совершает колебания в упругой среде, то оно воздействует на частицы среды, заставляя их совершать вынужденные колебания.
Упругие волны распространяются в упругой среде.
Основное свойство волн –перенос импульса и энергии без переноса вещества
При распространении волны, частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия
Вместе с волной от частицы к частице, передается лишь состояние колебательного движения и его энергия

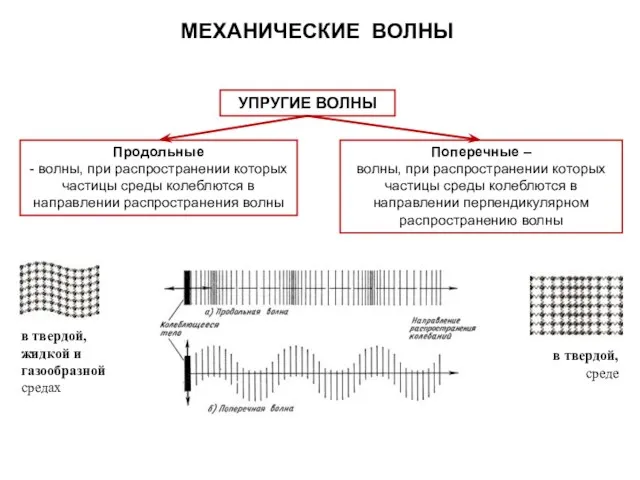
МЕХАНИЧЕСКИЕ ВОЛНЫ
Среди волн, встречающихся в природе и технике, выделяются их типы: волны на поверхности жидкости, упругие и электромагнитные волны
Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде (звуковые и сейсмические волны (колебания, распространяющиеся в Земле от очагов землетрясений, взрывов и других источников))
Волны на поверхности жидкости (поверхностные волны) – это распространяющиеся вдоль свободной поверхности жидкости (или поверхности раздела двух несмешивающихся жидкостей) возмущения этой поверхности, возникающие под влиянием внешних воздействий (падения тел, движения судов, ветра и тому подобное). В образовании и распространении этих волн определяющую роль играют силы поверхностного натяжения и тяжести.

МЕХАНИЧЕСКИЕ ВОЛНЫ
в твердой, жидкой и газообразной средах
в твердой, среде

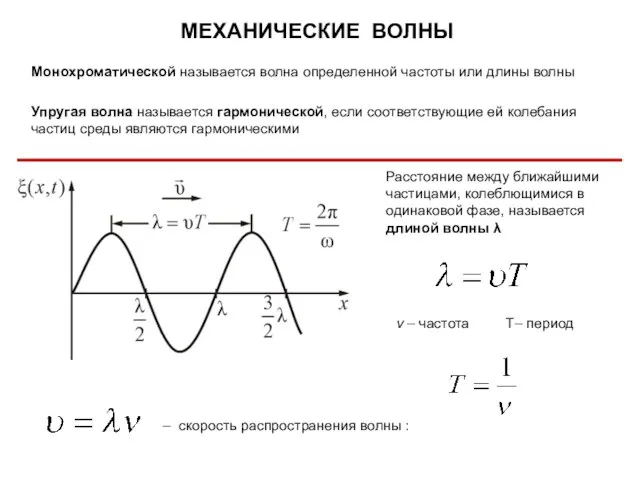
Монохроматической называется волна определенной частоты или длины волны
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны λ
ν – частота
Т– период
– скорость распространения волны :
МЕХАНИЧЕСКИЕ ВОЛНЫ

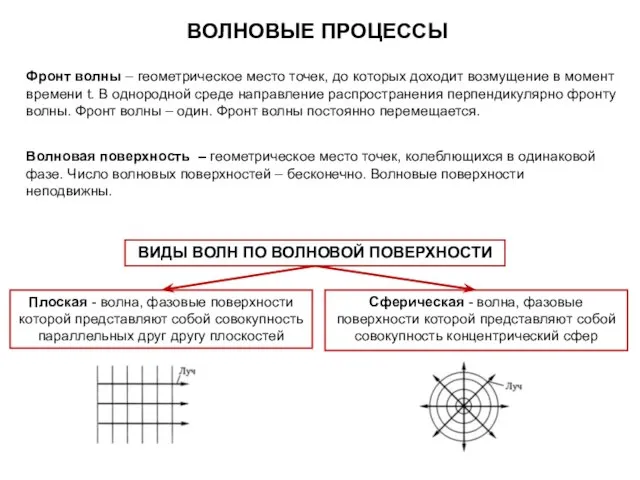
ВОЛНОВЫЕ ПРОЦЕССЫ
Фронт волны – геометрическое место точек, до которых доходит возмущение в момент времени t. В однородной среде направление распространения перпендикулярно фронту волны. Фронт волны – один. Фронт волны постоянно перемещается.
Волновая поверхность ‒ геометрическое место точек, колеблющихся в одинаковой фазе. Число волновых поверхностей – бесконечно. Волновые поверхности неподвижны.
ВИДЫ ВОЛН ПО ВОЛНОВОЙ ПОВЕРХНОСТИ
Плоская - волна, фазовые поверхности которой представляют собой совокупность параллельных друг другу плоскостей
Сферическая - волна, фазовые поверхности которой представляют собой совокупность концентрический сфер

Уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид (общий случай)
где А=сопst - амплитуда волны,
ω - циклическая частота,
ϕ0 - начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t,
- фаза плоской волны
УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ
Выражение определяет связь между временем (t) и тем местом (x), в котором зафиксировано определенное значение фазы
Таким образом, скорость распространения волны υ в уравнении - есть скорость перемещения фазы, в связи, с чем ее называют фазовой скоростью

Для характеристики волн используют волновое число
Тогда уравнение плоской волны запишется так
Скорость распространения волны (скорость перемещения фазы волны), называют фазовой скоростью. Из формулы для волнового числа получим формулу для фазовой скорости
Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой
УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ

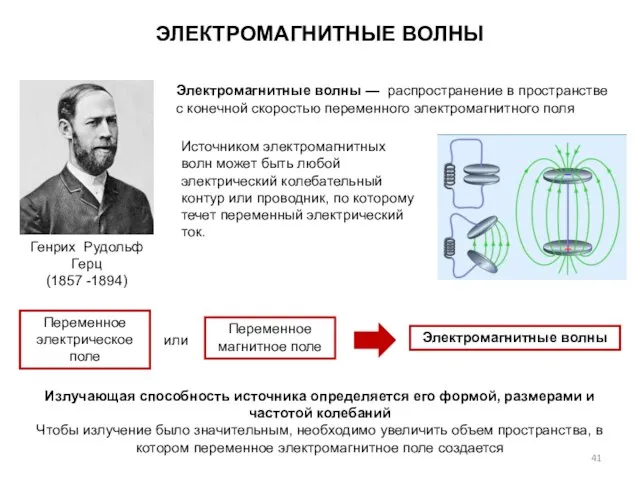
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Генрих Рудольф Герц
(1857 -1894)
Источником электромагнитных волн может быть любой электрический колебательный контур или проводник, по которому течет переменный электрический ток.
Излучающая способность источника определяется его формой, размерами и частотой колебаний
Чтобы излучение было значительным, необходимо увеличить объем пространства, в котором переменное электромагнитное поле создается
Переменное электрическое поле
Переменное магнитное поле
или
Электромагнитные волны
Электромагнитные волны — распространение в пространстве с конечной скоростью переменного электромагнитного поля

Скорость распространения электромагнитных волн в среде зависит от ее электрической и магнитной проницаемостей.
абсолютный показатель преломления
и
показатель преломления есть физическая величина, равная отношению скорости электромагнитных волн в вакууме к их скорости в среде
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

1820 год Ампер открыл закон, показывающий, что электрический ток производит магнитное поле.
1831 год Фарадей открыл закон электромагнитной индукции.
1864 год Максвелл создал теорию электромагнитного поля.
1888 год Герц подтвердил существование электромагнитного поля.
1891 год Тесла улучшил и запатентовал передатчик волн Герца для радиочастотного энергоснабжения.
1894 год Тесла зажёг без проводов фосфорную лампу накаливания.
1894 год Боше дистанционно воспламенил порох, показывая, что сигналы связи можно посылать без проводов.
25 апреля (7 мая) 1895 года А. Попов продемонстрировал изобретённый им радиоприёмник и передал сигнал на 50 км.
2 июня 1896 года Маркони подал заявку на изобретение радио.
2009 год норвежская компания «Wireless Power & Communication» представила фонарь, способный безопасно работать и перезаряжаться бесконтактным способом.
2009 год фирма «Haier Group» представила первый в мире полностью беспроводной LCD-телевизор, основанный на беспроводной передаче энергии.
2015 год учёные из Вашингтонского университета выяснили, что электричество можно передавать посредством технологии Wi-Fi.
2017 год учёные того же университета создали прототип мобильного телефона без батареи.
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

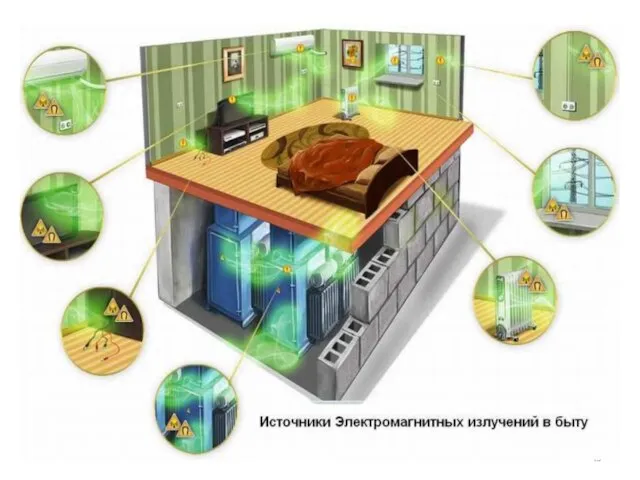
ПРИМЕНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
С помощью спектрального анализа
открывают новые элементы (рубидий, цезий и др.)
узнали химический состав Солнца и звезд
определяют состав руд и металлов
Спектральный анализ является основным методом контроля в металлургии, машиностроении, атомной промышленности.

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ