Содержание
- 5. Внутренние потребности теоретической математики (математическая логика, алгебра, геометрия и анализ). Создание быстродействующих электронных вычислительных и управляющих
- 6. Определение алгоритма через понятие вычислительной машины (машины Тьюринга, предложено Тьюрингом в 1937г. и машины Поста в
- 7. слово “алгоритм” является производным от имени среднеазиатского ученого Аль Хорезми, уроженца Хивы, жившего в IX веке
- 8. Предписание считается алгоритмом, если оно обладает следующими свойствами: Каждый алгоритм, в общем случае, должен задаваться следующими
- 9. Есть проблемы, для которых алгоритм вообще не может существовать. задача точного определения понятия алгоритма Все проблемы
- 10. Готфрид Вильгельм Лейбниц 1646 —1716 немецкий философ, математик, физик создал математический анализ - дифференциальное и интегральное
- 11. Найти алгоритм, определяющий для любого диафантова уравнения, имеет ли оно целочисленное решение. Диафантово уравнение есть уравнение
- 12. Каждый шаг алгоритма таков, что его может выполнить достаточно простое устройство (машина). Желательно, чтобы это устройство
- 13. Эмиль Леон Пост (Emil Leon Post) 1897 - 1954 американский математик и логик один из основателей
- 14. Машина Поста — абстрактная вычислительная машина, состоящая из каретки (считывающей и записывающей головки) и ленты, разбитой
- 15. 1. → j – переместить каретку вправо на 1 ячейку и перейти к строке с номером
- 16. Алан Тьюринг (Alan Mathison Turing) 1912 - 1954 Английский математик, логик. Ввёл математическое понятие абстрактного эквивалента
- 17. Задача описания алгоритма может быть сведена к построению машины некоторого типа, которая способна воспринимать набор правил,
- 18. С помощью машины Тьюринга можно доказать существование или не существование алгоритмов решения различных задач. заданная система
- 19. Под одноленточной машиной Тьюринга понимают кибернетическое устройство, состоящее из следующих элементов: бесконечной ленты, разделенной на ячейки,
- 20. Поскольку бесконечную ленту физически смоделировать затруднительно, обычно предполагается, что она конечная, и разбита на конечное число
- 21. Управляющая головка – это некоторое устройство, которое может перемещаться вдоль ленты так, что в каждый рассматриваемый
- 22. Предполагается, что число возможных состояний внутренней памяти конечное и для каждой машины фиксированное. Состояние внутренней памяти
- 23. Если в какой-то момент времени внутренняя память машины приходит в заключительное состояние Ω, то дальнейших изменений
- 24. Предполагается, что машина снабжена особым механизмом, который в зависимости от символа в воспринимаемой ячейке и состояния
- 25. Конфигурация машины Тьюринга – совокупность, образованная содержимым текущей обозреваемой ячейки aj и состоянием внутренней памяти Si.
- 26. Программа машины Тьюринга – совокупность команд установленного формата Так как работа машины по условию целиком определяется
- 27. видео LEGO Turing Machine - YouTube Машина Тьюринга была построена в металле в 1973 в Малой
- 28. Тезис Тьюринга – любой алгоритм можно преобразовать в машину Тьюринга. Эту гипотезу невозможно доказать, потому что
- 29. Мальцев А.И. Алгоритмы и рекурсивные функции. М.: Наука, 1965, 1986. М.Минский. Вычисления и автоматы. М.: Мир,
- 31. Скачать презентацию


























 Вычисление площадей плоских фигур в прямоугольной системе координат (Лекция 3)
Вычисление площадей плоских фигур в прямоугольной системе координат (Лекция 3) Задача о расшивке узких мест производства
Задача о расшивке узких мест производства Внеклассное мероприятие. 5 класс
Внеклассное мероприятие. 5 класс Создание геометрических тел
Создание геометрических тел Содержание функциональной пропедевтики в начальной школе, 5–6-х классах, в начале курса алгебры
Содержание функциональной пропедевтики в начальной школе, 5–6-х классах, в начале курса алгебры История возникновения геометрии как науки
История возникновения геометрии как науки Решение задач
Решение задач Элементы теории обобщенных функций
Элементы теории обобщенных функций Презентация на тему НАХОЖДЕНИЕ СУММЫ НЕСКОЛЬКИХ СЛАГАЕМЫХ
Презентация на тему НАХОЖДЕНИЕ СУММЫ НЕСКОЛЬКИХ СЛАГАЕМЫХ  Степень с рациональным показателем. Множество рациональных чисел
Степень с рациональным показателем. Множество рациональных чисел Стереометрия. 1
Стереометрия. 1 Функция у=х в степени -n (n є N), их свойства и графики
Функция у=х в степени -n (n є N), их свойства и графики Неравенство треугольника
Неравенство треугольника Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс)
Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс) Алгоритм отыскания производной
Алгоритм отыскания производной Свойства квадратного корня
Свойства квадратного корня Степень с целым показателем ( урок обобщения и систематизации в форме игры крестики – нолики)
Степень с целым показателем ( урок обобщения и систематизации в форме игры крестики – нолики) Презентация на тему ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
Презентация на тему ЦЕНТРАЛЬНАЯ СИММЕТРИЯ  Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА
Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА  Понятие множество
Понятие множество Способы задания плоскости
Способы задания плоскости Интерактивная игра уроки математики в Школе Смешариков
Интерактивная игра уроки математики в Школе Смешариков Справедливые и несправедливые игры с точки зрения теории вероятностей
Справедливые и несправедливые игры с точки зрения теории вероятностей Занимательная математика. 2 класс
Занимательная математика. 2 класс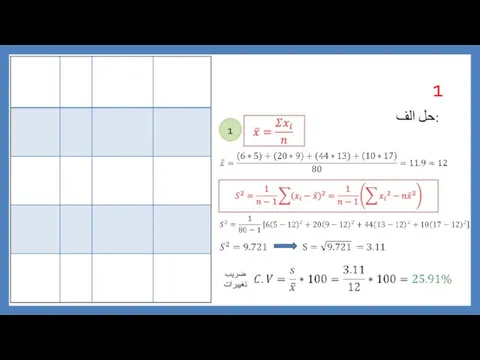 حل تمرین آمار
حل تمرین آمار История возникновения науки геометрии
История возникновения науки геометрии Презентация на тему История возникновения счета
Презентация на тему История возникновения счета  Prezentatsia_k_uroku_matematiki_v_6_kl
Prezentatsia_k_uroku_matematiki_v_6_kl