Решение задач на расчет статически определимых плоских ферм путем построения диаграммы Масквелла-Кремоны
- Главная
- Физика
- Решение задач на расчет статически определимых плоских ферм путем построения диаграммы Масквелла-Кремоны

Содержание
- 2. 3. Решение. 3.1. Вычерчиваем геометрическую схему фермы в масштабе, например 1: 100 . 3.2. Обозначим поля:
- 3. 3.3. Определяем опорные реакции фермы: а) выбираем масштаб сил: в 1 см – 15 кН; б)
- 4. 3. 4. Строим диаграмму усилий: а) мысленно вырезаем узел А, в котором сходятся два стержня, которые
- 5. Точку пересечения этих линий обозначим цифрой 3, соответствующей полю, которое лежит между стержнями 2—3 и 3-е.
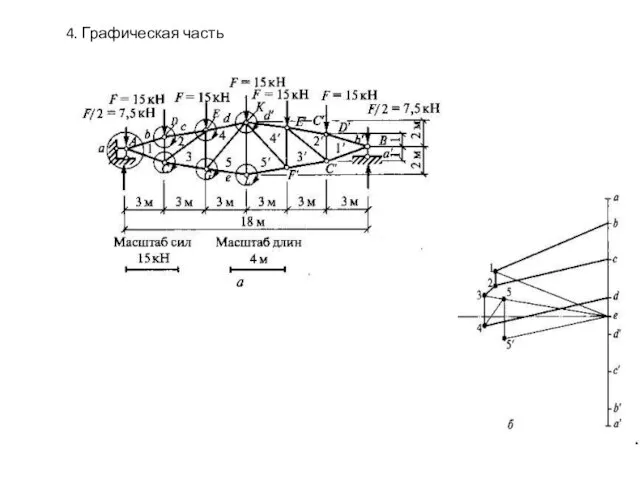
- 6. 4. Графическая часть
- 8. Скачать презентацию
Слайд 2
3. Решение.
3.1. Вычерчиваем геометрическую схему фермы в масштабе, например 1:
3. Решение.
3.1. Вычерчиваем геометрическую схему фермы в масштабе, например 1:
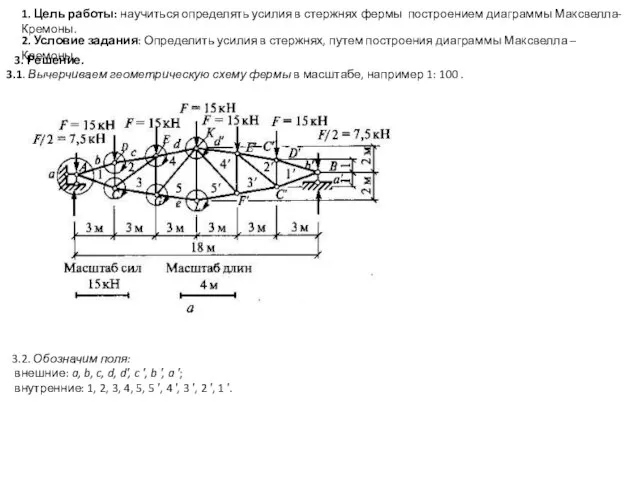
100 .
3.2. Обозначим поля:
внешние: a, b, c, d, d′, c ′, b ′, a ′;
внутренние: 1, 2, 3, 4, 5, 5 ′, 4 ′, 3 ′, 2 ′, 1 ′.
3.2. Обозначим поля:
внешние: a, b, c, d, d′, c ′, b ′, a ′;
внутренние: 1, 2, 3, 4, 5, 5 ′, 4 ′, 3 ′, 2 ′, 1 ′.
2. Условие задания: Определить усилия в стержнях, путем построения диаграммы Максвелла – Кремоны
1. Цель работы: научиться определять усилия в стержнях фермы построением диаграммы Максвелла-Кремоны.
Слайд 3 3.3. Определяем опорные реакции фермы:
а) выбираем масштаб сил: в 1
3.3. Определяем опорные реакции фермы:
а) выбираем масштаб сил: в 1
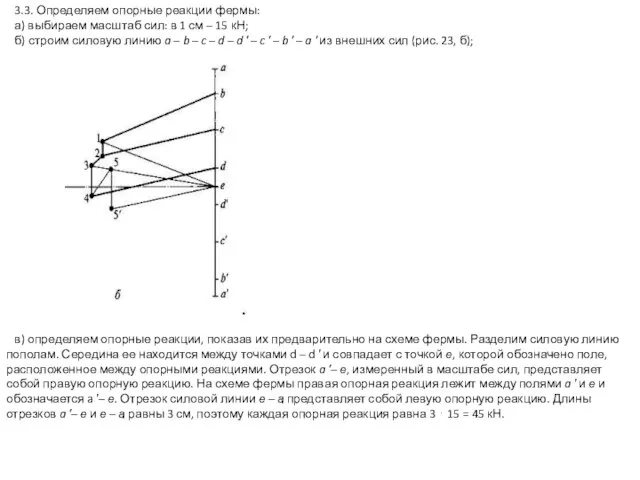
см – 15 кН;
б) строим силовую линию a – b – c – d – d ′ – c ′ – b ′ – a ′ из внешних сил (рис. 23, б);
в) определяем опорные реакции, показав их предварительно на схеме фермы. Разделим силовую линию
пополам. Середина ее находится между точками d – d ′ и совпадает с точкой е, которой обозначено поле,
расположенное между опорными реакциями. Отрезок a ′– е, измеренный в масштабе сил, представляет
собой правую опорную реакцию. На схеме фермы правая опорная реакция лежит между полями a ′ и е и
обозначается a ′– е. Отрезок силовой линии е – а представляет собой левую опорную реакцию. Длины
отрезков a ′– е и е – а равны 3 см, поэтому каждая опорная реакция равна 3 ⋅ 15 = 45 кН.
б) строим силовую линию a – b – c – d – d ′ – c ′ – b ′ – a ′ из внешних сил (рис. 23, б);
в) определяем опорные реакции, показав их предварительно на схеме фермы. Разделим силовую линию
пополам. Середина ее находится между точками d – d ′ и совпадает с точкой е, которой обозначено поле,
расположенное между опорными реакциями. Отрезок a ′– е, измеренный в масштабе сил, представляет
собой правую опорную реакцию. На схеме фермы правая опорная реакция лежит между полями a ′ и е и
обозначается a ′– е. Отрезок силовой линии е – а представляет собой левую опорную реакцию. Длины
отрезков a ′– е и е – а равны 3 см, поэтому каждая опорная реакция равна 3 ⋅ 15 = 45 кН.
Слайд 4 3. 4. Строим диаграмму усилий:
а) мысленно вырезаем узел А, в
3. 4. Строим диаграмму усилий:
а) мысленно вырезаем узел А, в

котором сходятся два стержня, которые назовем b – 1 и 1 – е.
на силовой линии уже есть точки b и е. Проведем через точку b линию, параллельную стержню b – 1,
а через точку е – линию, параллельную стержню 1 – е. Точку их пересечения обозначим цифрой 1.
Длина линии b – 1 равна 3,8 см. Помня, что в принятом масштабе 1 см = 15 кН, получим усилие в стержне
b – 1, равное 3,8 ⋅ 15 = 57 кН. Длина линии 1 – е также равна 3,8 см, т.е.усилие 1 – е тоже равно 57 кН.
Определим знак усилия b – 1: на схеме фермы (см. рис. 23, а) стержень верхнего пояса читается b – 1;
на диаграмме усилий (см. рис. 23, б) движение от точки b к точке 1 направлено справа налево.
Перенесем это направление движения (справа налево) на стержень b – 1 (см. рис. 23, а) – оно
направлено к узлу, т.е. стержень сжат. Усилие b – 1 обозначено жирной линией. Определим
знак усилия 1 – е: на схеме фермы стержень читается 1 – е; на диаграмме усилий движение от точки 1
к точке е направлено слева направо. Перенесем это направление движения на стержень фермы
оно направлено от узла, т.е. стержень растянут. Усилие 1 – е на диаграмме обозначено тонкой линией;
б) вырезаем узел D. В нем сходятся три стержня: 1 – b, с – 2 и 2 – 1. Усилие в стержне 1 – b найдено из
рассмотрения узла А, а усилия в стержнях с – 2 и 2 – 1 неизвестны. На диаграмме усилий уже есть точки
с и 1. Проведем через точку с линию, параллельную стержню с – 2, а через точку 1 – линию, параллельную
стержню 2 – 1, до взаимного пересечения. Точку пересечения линий обозначим цифрой 2 (номером поля,
которое лежит между стержнями, усилия в которых отыскиваются). Отрезок с – 2 равен 3,65 см, следова-
тельно, усилие в нем равно 3,65 ⋅ 15 = 54,8 кН. Отрезок 2 – 1 равен 0,4 см, усилие в нем равно 0,4 ⋅ 15 = 6 кН.
Определим знак усилия в стержне с – 2: на схеме фермы стержень читается с – 2; на диаграмме усилий
движение от точки с к точке 2 направлено справа на лево; перенесем это направление движения на
стержень с – 2 – оно направлено к узлу D, т.е. стержень сжат (на диаграмме усилие показано жирной
линией).
Определим знак усилия 2—1: на схеме фермы стержень читается 2— 1; на диаграмме усилий движение от
точки 2 к точке 1 направлено снизу вверх. Перенесем это движение на стержень 2—1 — оно направлено к
узлу D, т. е. стержень сжат (на диаграмме усилие показано жирной линией);
в)рассмотрим узел С. В этом узле сходятся четыре стержня, причем усилия в двух из них (е— 1 и 1—2) уже определены, а в двух(2—3 и 3-е) неизвестны. На диаграмме усилий уже есть точки 2 и е. Проведем через
точку 2 линию, параллельную стержню 2—3,а через точку е — линию, параллельную стержню 3-е.
на силовой линии уже есть точки b и е. Проведем через точку b линию, параллельную стержню b – 1,
а через точку е – линию, параллельную стержню 1 – е. Точку их пересечения обозначим цифрой 1.
Длина линии b – 1 равна 3,8 см. Помня, что в принятом масштабе 1 см = 15 кН, получим усилие в стержне
b – 1, равное 3,8 ⋅ 15 = 57 кН. Длина линии 1 – е также равна 3,8 см, т.е.усилие 1 – е тоже равно 57 кН.
Определим знак усилия b – 1: на схеме фермы (см. рис. 23, а) стержень верхнего пояса читается b – 1;
на диаграмме усилий (см. рис. 23, б) движение от точки b к точке 1 направлено справа налево.
Перенесем это направление движения (справа налево) на стержень b – 1 (см. рис. 23, а) – оно
направлено к узлу, т.е. стержень сжат. Усилие b – 1 обозначено жирной линией. Определим
знак усилия 1 – е: на схеме фермы стержень читается 1 – е; на диаграмме усилий движение от точки 1
к точке е направлено слева направо. Перенесем это направление движения на стержень фермы
оно направлено от узла, т.е. стержень растянут. Усилие 1 – е на диаграмме обозначено тонкой линией;
б) вырезаем узел D. В нем сходятся три стержня: 1 – b, с – 2 и 2 – 1. Усилие в стержне 1 – b найдено из
рассмотрения узла А, а усилия в стержнях с – 2 и 2 – 1 неизвестны. На диаграмме усилий уже есть точки
с и 1. Проведем через точку с линию, параллельную стержню с – 2, а через точку 1 – линию, параллельную
стержню 2 – 1, до взаимного пересечения. Точку пересечения линий обозначим цифрой 2 (номером поля,
которое лежит между стержнями, усилия в которых отыскиваются). Отрезок с – 2 равен 3,65 см, следова-
тельно, усилие в нем равно 3,65 ⋅ 15 = 54,8 кН. Отрезок 2 – 1 равен 0,4 см, усилие в нем равно 0,4 ⋅ 15 = 6 кН.
Определим знак усилия в стержне с – 2: на схеме фермы стержень читается с – 2; на диаграмме усилий
движение от точки с к точке 2 направлено справа на лево; перенесем это направление движения на
стержень с – 2 – оно направлено к узлу D, т.е. стержень сжат (на диаграмме усилие показано жирной
линией).
Определим знак усилия 2—1: на схеме фермы стержень читается 2— 1; на диаграмме усилий движение от
точки 2 к точке 1 направлено снизу вверх. Перенесем это движение на стержень 2—1 — оно направлено к
узлу D, т. е. стержень сжат (на диаграмме усилие показано жирной линией);
в)рассмотрим узел С. В этом узле сходятся четыре стержня, причем усилия в двух из них (е— 1 и 1—2) уже определены, а в двух(2—3 и 3-е) неизвестны. На диаграмме усилий уже есть точки 2 и е. Проведем через
точку 2 линию, параллельную стержню 2—3,а через точку е — линию, параллельную стержню 3-е.
Слайд 5 Точку пересечения этих линий обозначим цифрой 3, соответствующей полю, которое лежит
Точку пересечения этих линий обозначим цифрой 3, соответствующей полю, которое лежит

между
стержнями 2—3 и 3-е. Длина линии 2—3 на диаграмме равна 0,45 см. Это значит, что усилие в стержне
2—3 равно 0,45 • 15 = 6,75 кН. Длина линии 3-е равна 4 см, т.е. усилие в стержне 3-е равно 4 • 15 = 60 кН.
Определим знак усилия 2—3: на схеме стержень фермы читается 2—3; на диаграмме усилий движение от
точки 2 к точке 3 направлено сверху вниз. Перенесем это движение на стержень 2—3 — оно направлено к
узлу С, т. е. стержень сжат (на диаграмме — жирная линия). Определим знак усилия 3-е: стержень нижнего
пояса читается 3-е; на диаграмме усилий движение от точки 3 к точке е направлено слева направо. Перенесем
это движение на стержень 3-е — оно направлено от узла С, т. е. стержень растянут (на диаграмме — тонкая
линия);
г)рассмотрим узел Е. В этом узле неизвестны усилия в стержнях d —4 и 4—3. На диаграмме проводим через
точки d и 3 линии, параллельные стержням d— 4 и 4—3, до пересечения в точке, которую обозначим цифрой 4.
Усилие в стержне d— 4 равно 4 • 15 = 60 кН, а в стержне 4—3 — 0,8 • 15 = 12 кН. Оба стержня сжаты;
д) узел G. В нем неизвестны усилия 4—5 и 5—е. На диаграмме проводим линии через точки 4 и е параллельно стержням 4—5 и 5—е, получим точку 5. Усилие в стержне 4—5 равно 0,9 • 15 == 13,5 кН (он растянут), в
стержне 5—е — 3,4 -15 = 51 кН (тоже растянут);
е) узел L. В нем неизвестны усилия в стержнях 5—5' и 5'—е. На диаграмме проводим линии параллельно этим стержням через точки 5 и е, получим точку 5'. Усилие в стержне 5—5' равно 1,1 • 15 == 16,5 кН (он растянут). Из диаграммы видно, что линия е—5‘ симметрична линии е —5 (или точка 5' расположена симметрично точке 5 относительно горизонтальной линии, проходящей через точку е).
На этом можно закончить построение диаграммы, так как усилия в симметричных стержнях одинаковы. Заполним таблицу усилий (табл. 1).
стержнями 2—3 и 3-е. Длина линии 2—3 на диаграмме равна 0,45 см. Это значит, что усилие в стержне
2—3 равно 0,45 • 15 = 6,75 кН. Длина линии 3-е равна 4 см, т.е. усилие в стержне 3-е равно 4 • 15 = 60 кН.
Определим знак усилия 2—3: на схеме стержень фермы читается 2—3; на диаграмме усилий движение от
точки 2 к точке 3 направлено сверху вниз. Перенесем это движение на стержень 2—3 — оно направлено к
узлу С, т. е. стержень сжат (на диаграмме — жирная линия). Определим знак усилия 3-е: стержень нижнего
пояса читается 3-е; на диаграмме усилий движение от точки 3 к точке е направлено слева направо. Перенесем
это движение на стержень 3-е — оно направлено от узла С, т. е. стержень растянут (на диаграмме — тонкая
линия);
г)рассмотрим узел Е. В этом узле неизвестны усилия в стержнях d —4 и 4—3. На диаграмме проводим через
точки d и 3 линии, параллельные стержням d— 4 и 4—3, до пересечения в точке, которую обозначим цифрой 4.
Усилие в стержне d— 4 равно 4 • 15 = 60 кН, а в стержне 4—3 — 0,8 • 15 = 12 кН. Оба стержня сжаты;
д) узел G. В нем неизвестны усилия 4—5 и 5—е. На диаграмме проводим линии через точки 4 и е параллельно стержням 4—5 и 5—е, получим точку 5. Усилие в стержне 4—5 равно 0,9 • 15 == 13,5 кН (он растянут), в
стержне 5—е — 3,4 -15 = 51 кН (тоже растянут);
е) узел L. В нем неизвестны усилия в стержнях 5—5' и 5'—е. На диаграмме проводим линии параллельно этим стержням через точки 5 и е, получим точку 5'. Усилие в стержне 5—5' равно 1,1 • 15 == 16,5 кН (он растянут). Из диаграммы видно, что линия е—5‘ симметрична линии е —5 (или точка 5' расположена симметрично точке 5 относительно горизонтальной линии, проходящей через точку е).
На этом можно закончить построение диаграммы, так как усилия в симметричных стержнях одинаковы. Заполним таблицу усилий (табл. 1).
Слайд 64. Графическая часть
4. Графическая часть
- Предыдущая
Мастер-класс Букет сирени 2_Волны
2_Волны Электрический ток
Электрический ток Термодинамика однокомпонентных систем
Термодинамика однокомпонентных систем Электромагнитная индукция
Электромагнитная индукция Определение тока и напряжения в идеальных элементах
Определение тока и напряжения в идеальных элементах Радио - принцип радиосвязи
Радио - принцип радиосвязи Физика – одна из основных наук о природе
Физика – одна из основных наук о природе Технология ремонта резьбовых соединений
Технология ремонта резьбовых соединений Освещение помещения. Оптимизация энергозатрат
Освещение помещения. Оптимизация энергозатрат Они были первыми
Они были первыми Решение задач. Мощность
Решение задач. Мощность Презентация на тему Атмосфера Земли. Атмосферное давление
Презентация на тему Атмосфера Земли. Атмосферное давление  Основные теоремы о пределах. Раскрыте неопределенностей
Основные теоремы о пределах. Раскрыте неопределенностей Физикалық шама
Физикалық шама Закон Максвелла. Электромагнитное поле
Закон Максвелла. Электромагнитное поле Давление. Единицы давления
Давление. Единицы давления Основы постановки научного эксперимента. ЯМР-спектроскопия. (Лекция 8)
Основы постановки научного эксперимента. ЯМР-спектроскопия. (Лекция 8) 3_ЭМКолебания
3_ЭМКолебания Технологические процессы восстановления деталей и узлов сельскохозяйственной техники. Лекция 2
Технологические процессы восстановления деталей и узлов сельскохозяйственной техники. Лекция 2 Полная работа системы
Полная работа системы Электрическое поле (Лекция 2)
Электрическое поле (Лекция 2) Презентация на тему Принцип Гюйгенса. Закон отражение света
Презентация на тему Принцип Гюйгенса. Закон отражение света  Презентация на тему Звук, ультразвук, инфразвук и их использование
Презентация на тему Звук, ультразвук, инфразвук и их использование  Модуль Юнга
Модуль Юнга Индукция магнитного поля
Индукция магнитного поля Решение физических задач графическим способом
Решение физических задач графическим способом Основы электроники
Основы электроники Распространение электромагнитного излучения в молекулярной атмосфере
Распространение электромагнитного излучения в молекулярной атмосфере