Содержание
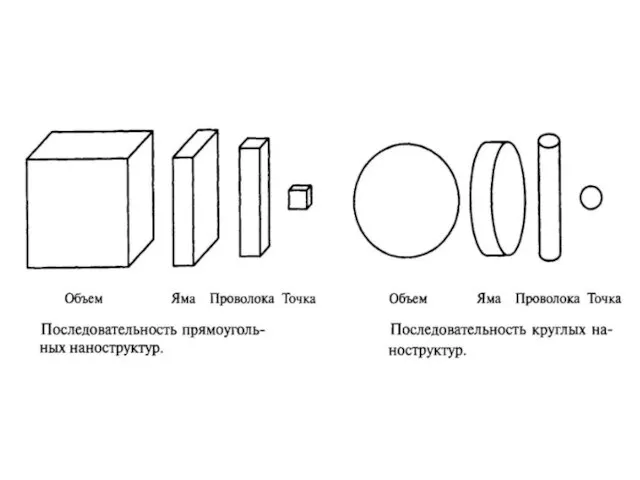
- 2. КВАНТОВЫЕ ЯМЫ, ПРОВОЛОКИ И ТОЧКИ При уменьшении размеров образца от больших (макроскопических) значений, например, метра или
- 3. Если размеры образца в одном измерении лежат в нанометровом диапазоне, а в двух других остаются большими,
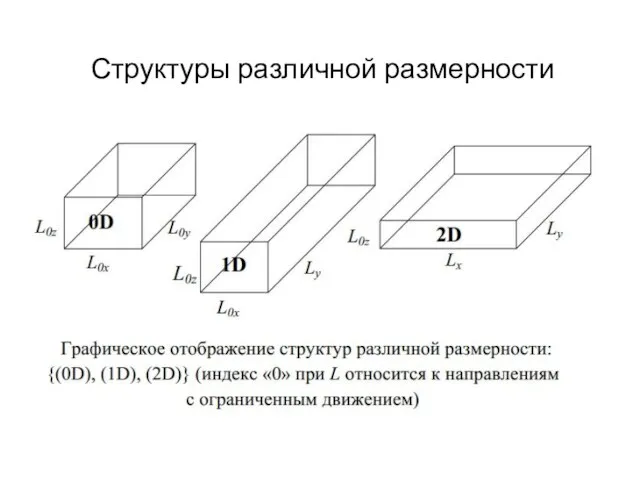
- 5. Структуры различной размерности
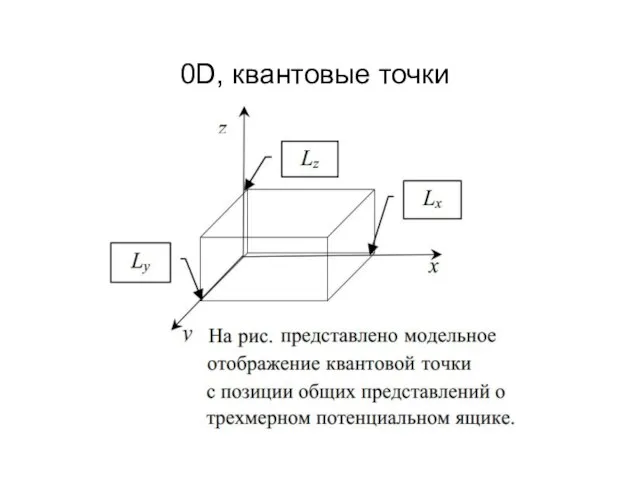
- 6. 0D, квантовые точки
- 11. Квантовые точки в полупроводниках. В полупроводниковых материалах между валентной зоной и зоной проводимости, как известно, существует
- 12. В первом приближении, поведение электронов в зоне проводимости и дырок в валентной зоне полупроводниковой частицы можно
- 13. Для сферического нанокристалла, например, энергии электронных и дырочных квантовых уровней, характеризующихся радиальным квантовым числом n и
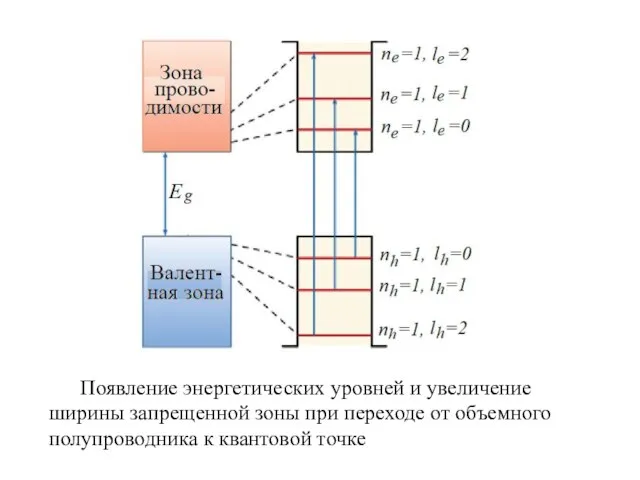
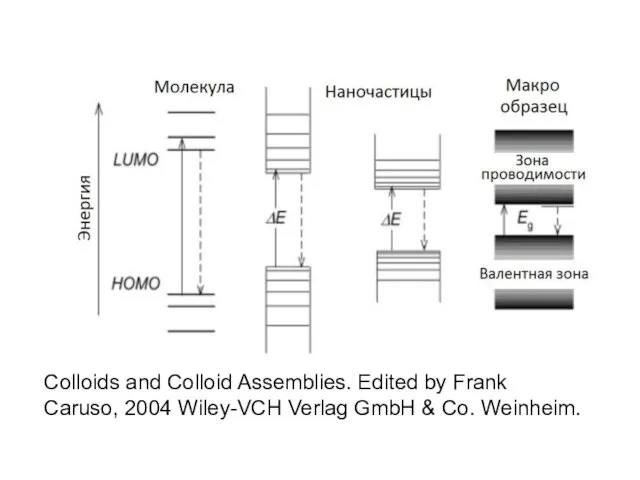
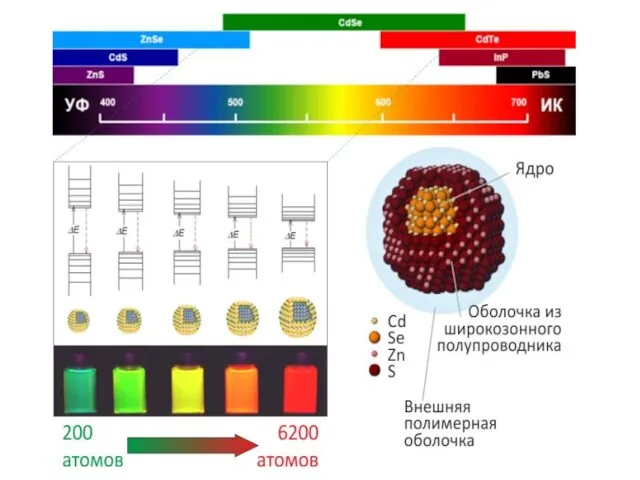
- 14. Появление энергетических уровней и увеличение ширины запрещенной зоны при переходе от объемного полупроводника к квантовой точке
- 15. При уменьшении радиуса кристалла увеличивается энергия электрона и дырки, и соответственно, растет наименьшая энергия оптического переход
- 16. Небольшой полупроводниковый кластер, состоящий только из нескольких атомов обладает лишь несколькими уровнями энергии (молекулярными орбиталями), доступными
- 17. Colloids and Colloid Assemblies. Edited by Frank Caruso, 2004 Wiley-VCH Verlag GmbH & Co. Weinheim.
- 18. Люминесценция. В полупроводниках в основном состоянии, как правило, электроны находятся в валентной зоне, в возбужденном состоянии
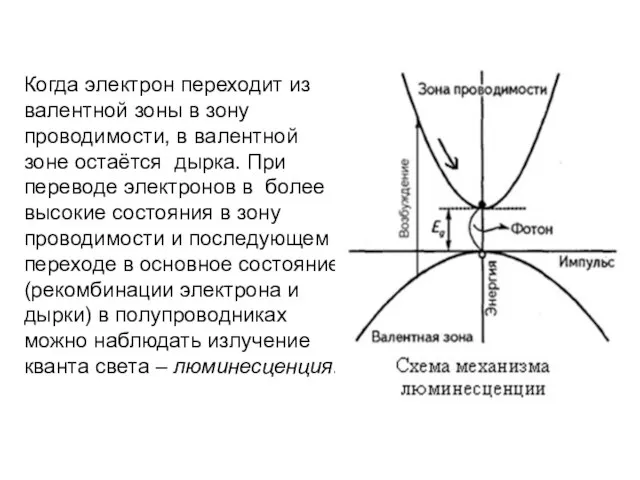
- 19. Когда электрон переходит из валентной зоны в зону проводимости, в валентной зоне остаётся дырка. При переводе
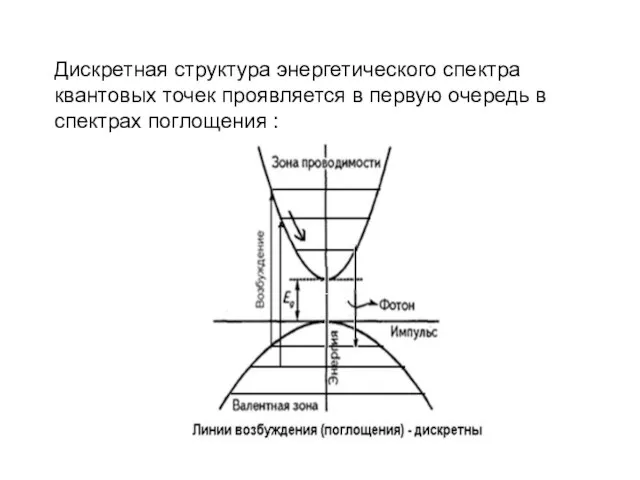
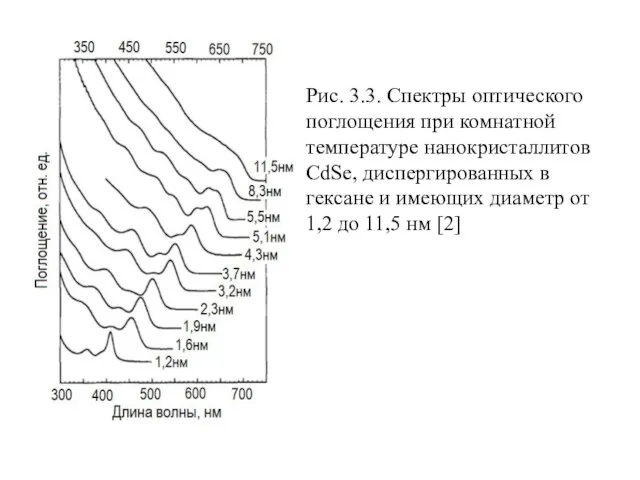
- 20. Дискретная структура энергетического спектра квантовых точек проявляется в первую очередь в спектрах поглощения :
- 22. В оптических явлениях квантово-размерный эффект проявляется не только в спектрах поглощения, но и в спектрах люминесценции,
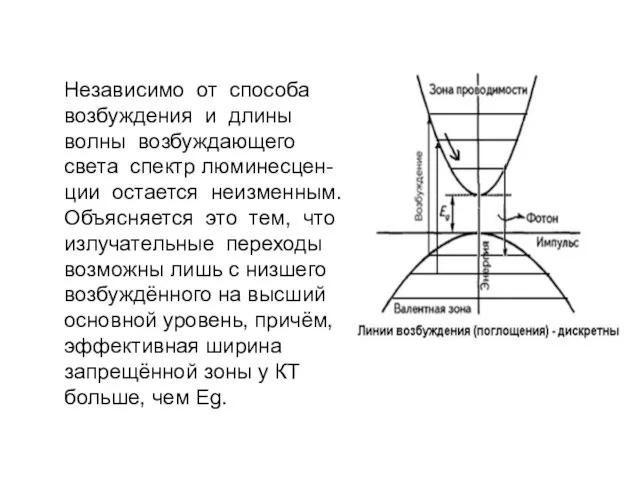
- 23. Независимо от способа возбуждения и длины волны возбуждающего света спектр люминесцен-ции остается неизменным. Объясняется это тем,
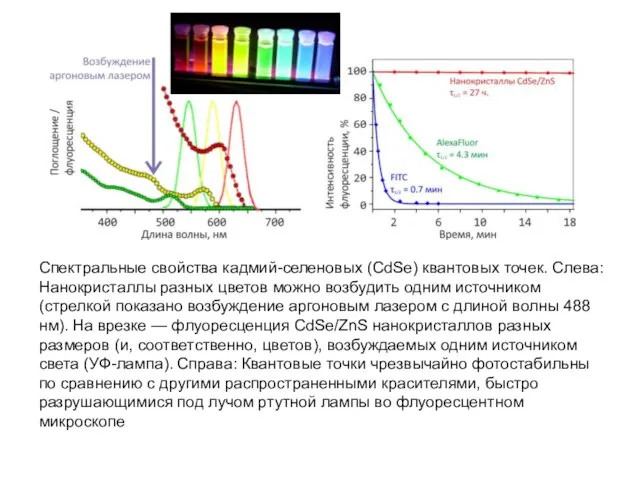
- 24. Спектральные свойства кадмий-селеновых (CdSe) квантовых точек. Слева: Нанокристаллы разных цветов можно возбудить одним источником (стрелкой показано
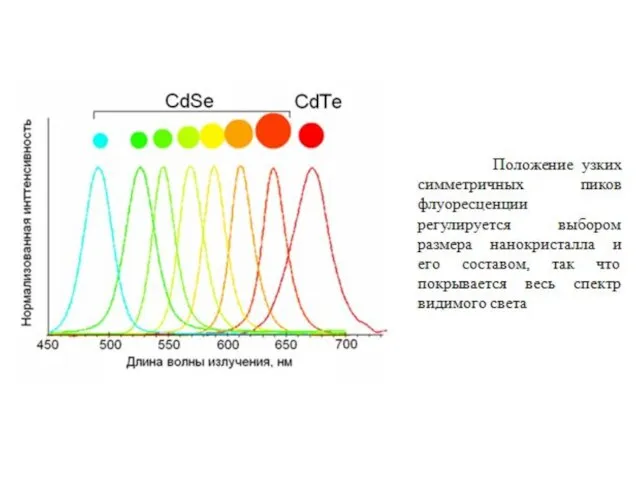
- 25. Нанокристаллы имеют уникальные оптические характеристики: узкий симметричный пик флуоресценции (в отличие от органических красителей, положение которого
- 28. Экситоны. Если энергия кванта света, падающего на кристалл, становится соизмеримой или превышает ширину его запрещенной зоны,
- 29. В кристалле энергия притяжения между электроном и дыркой, которую называют энергией связи экситона, задается соотношением, подобным
- 30. По аналогии с первым боровским радиусом атома водорода =0,53Å вводится боровский радиус экситона:
- 31. Экситоны в квантовых точках. Эффект изменения размера запрещенной зоны квантовой точки зависит от режима квантового ограничения
- 32. Однако, больший интерес вызывают квантовые точки в режиме «сильного удержания», которые меньше радиуса экситона Бора. В
- 33. В этом случае, полную энергию флуоресцирующего фотона можно моделировать как сумму запрещенной зоны квантовой точки, энергии
- 34. Если радиус квантовой точки а гораздо меньше aB, то такой экситон называется квантовой точкой малого радиуса.
- 36. Скачать презентацию





















 Явление тяготения. Сила тяжести
Явление тяготения. Сила тяжести Тест
Тест Оптика, квантовая оптика, квантовая механика
Оптика, квантовая оптика, квантовая механика Сила
Сила Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Электрический ток в жидкостях
Электрический ток в жидкостях Отсчёт по производственной практике
Отсчёт по производственной практике 2_kurs_lektsia_1_2
2_kurs_lektsia_1_2 Решение задач по кинематики
Решение задач по кинематики Проводники и диэлектрики
Проводники и диэлектрики В мире звуков
В мире звуков 实验五 功率放大电路
实验五 功率放大电路 Презентация на тему Изобретение радио Поповым (11 класс)
Презентация на тему Изобретение радио Поповым (11 класс)  Технология проверки технического состояния направляющих и ведущих колёс
Технология проверки технического состояния направляющих и ведущих колёс Решение многоуровневой задачи. Эйфелева башня
Решение многоуровневой задачи. Эйфелева башня Презентация на тему Деление ядер урана
Презентация на тему Деление ядер урана  Электростатика. Основы электромеханики
Электростатика. Основы электромеханики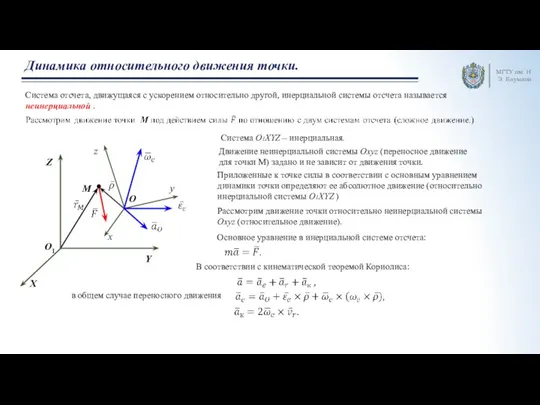 Динамика относительного движения точки. Лекция 2
Динамика относительного движения точки. Лекция 2 f3c279363c6051c6009ac4b1a3800ded
f3c279363c6051c6009ac4b1a3800ded Техническая механика
Техническая механика Квантовый протокол E91. Неравенства Белла
Квантовый протокол E91. Неравенства Белла Электромагнитная природа света
Электромагнитная природа света Сила трения
Сила трения Изобретение радио
Изобретение радио Искусственный интеллект. Сценарий №1
Искусственный интеллект. Сценарий №1 Плоская система сходящихся сил. Определение равнодействующей аналитическим способом
Плоская система сходящихся сил. Определение равнодействующей аналитическим способом Генератор 2ГВ-008
Генератор 2ГВ-008 Определение реакций связей твердого тела
Определение реакций связей твердого тела