Содержание
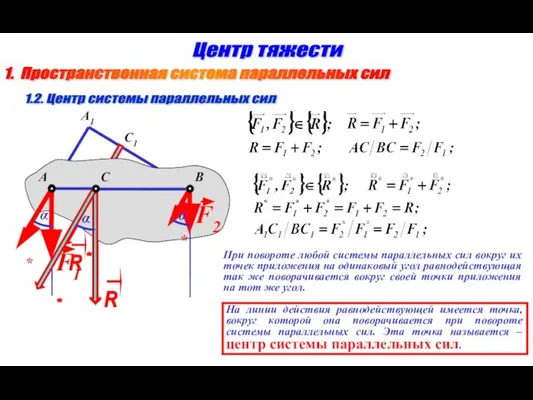
- 2. 1. Пространственная система параллельных сил Центр тяжести 1.2. Центр системы параллельных сил A B C α
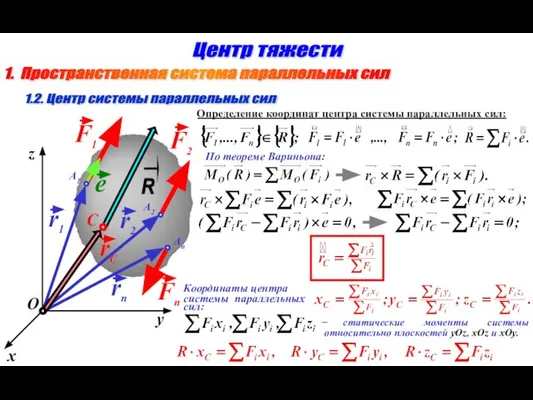
- 3. 1. Пространственная система параллельных сил Центр тяжести 1.2. Центр системы параллельных сил Определение координат центра системы
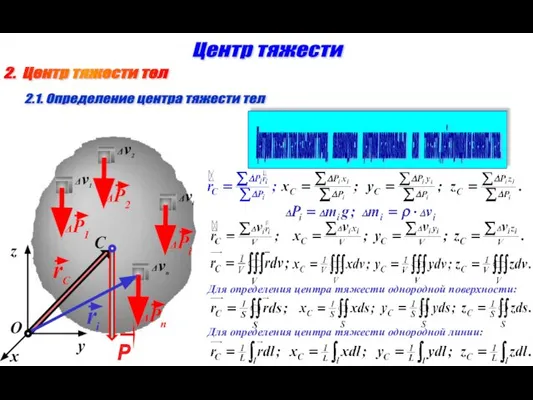
- 4. O x y z 2. Центр тяжести тел Центр тяжести 2.1. Определение центра тяжести тел Δv1
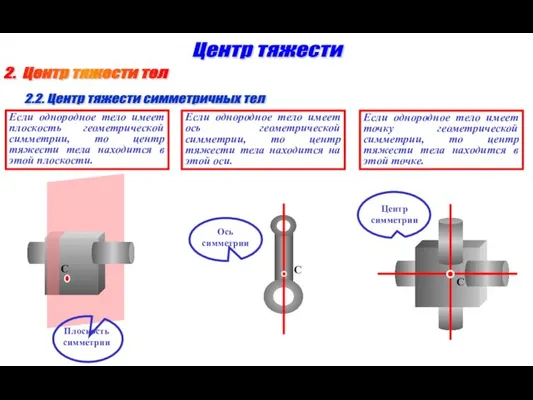
- 5. 2. Центр тяжести тел Центр тяжести 2.2. Центр тяжести симметричных тел Если однородное тело имеет плоскость
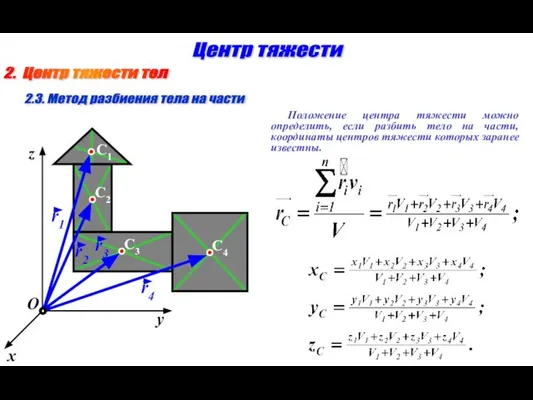
- 6. 2. Центр тяжести тел Центр тяжести 2.3. Метод разбиения тела на части С1 O x y
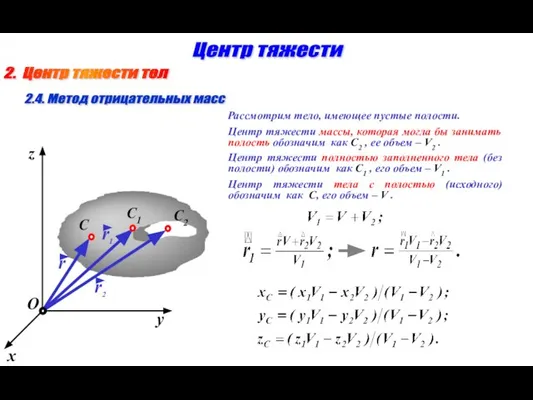
- 7. 2. Центр тяжести тел Центр тяжести 2.4. Метод отрицательных масс O x y z Рассмотрим тело,
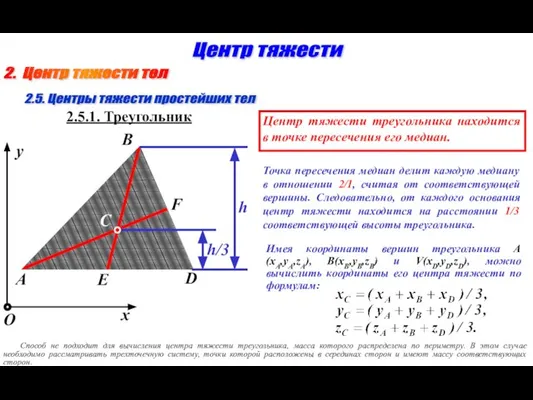
- 8. 2. Центр тяжести тел Центр тяжести 2.5. Центры тяжести простейших тел 2.5.1. Треугольник C A B
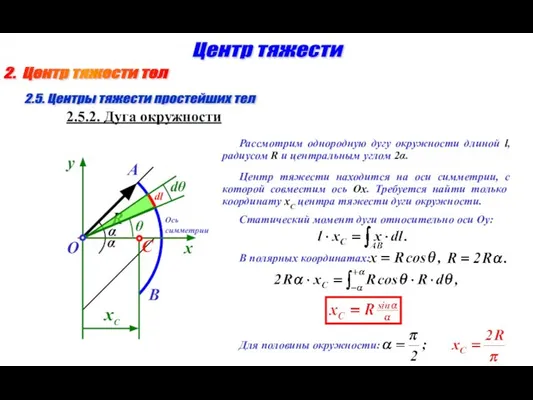
- 9. 2. Центр тяжести тел Центр тяжести R α α A B O Ось симметрии x y
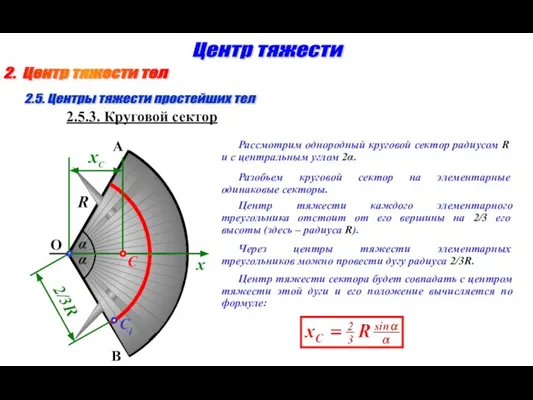
- 10. 2. Центр тяжести тел Центр тяжести Рассмотрим однородный круговой сектор радиусом R и с центральным углом
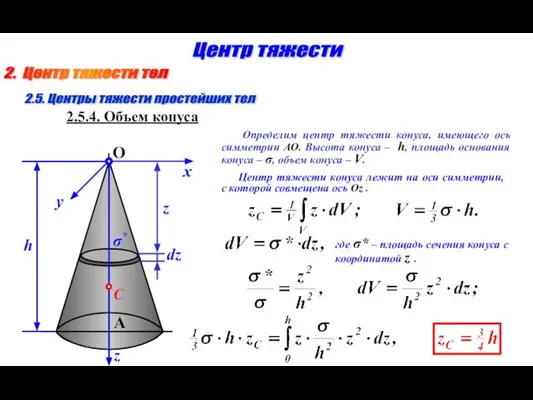
- 11. 2. Центр тяжести тел Центр тяжести Определим центр тяжести конуса, имеющего ось симметрии АО. Высота конуса
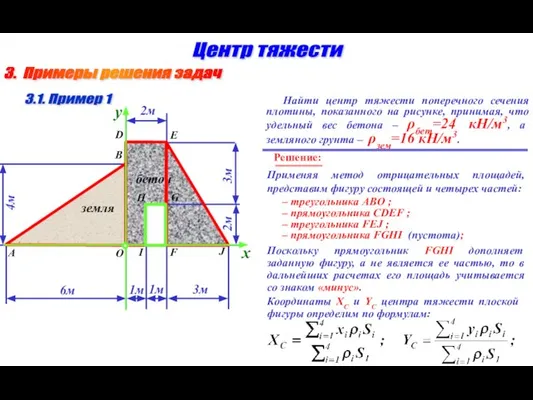
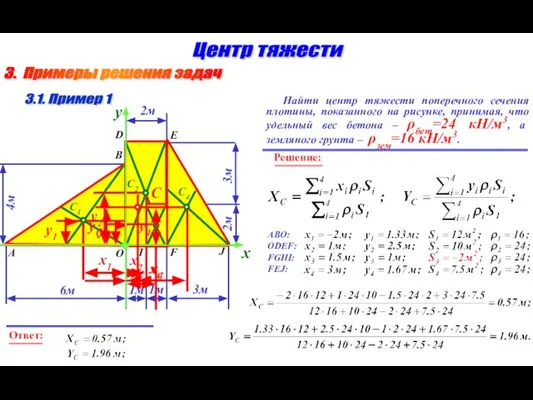
- 12. 3. Примеры решения задач Центр тяжести 3.1. Пример 1 Найти центр тяжести поперечного сечения плотины, показанного
- 13. 3. Примеры решения задач Центр тяжести 3.1. Пример 1 Найти центр тяжести поперечного сечения плотины, показанного
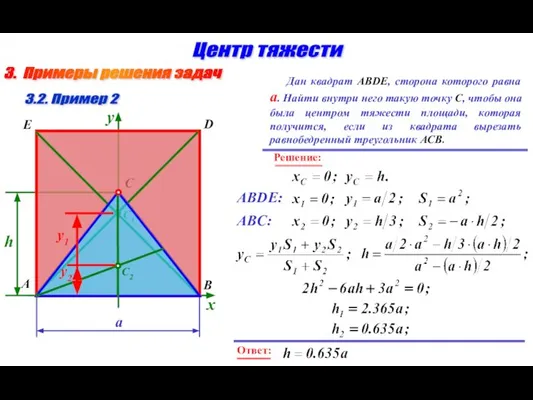
- 14. 3. Примеры решения задач Центр тяжести 3.2. Пример 2 Дан квадрат ABDE, сторона которого равна а.
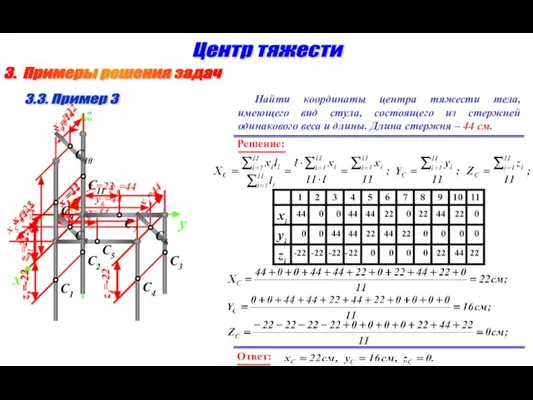
- 15. 3. Примеры решения задач Центр тяжести 3.3. Пример 3 Найти координаты центра тяжести тела, имеющего вид
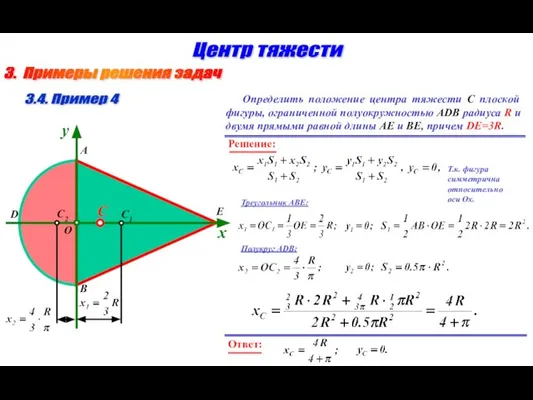
- 16. 3. Примеры решения задач Центр тяжести 3.4. Пример 4 Определить положение центра тяжести С плоской фигуры,
- 18. Скачать презентацию
 Фізичні основи оптикоелектронних систем. Тема 2
Фізичні основи оптикоелектронних систем. Тема 2 Вес тела. Единицы силы. Связь между силой тяжести и массой тела
Вес тела. Единицы силы. Связь между силой тяжести и массой тела Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения Посадочный размер блока. Диаметр ТЭНа
Посадочный размер блока. Диаметр ТЭНа Исследование физико-химических процессов получения порошковых покрытий газоплазменным методом
Исследование физико-химических процессов получения порошковых покрытий газоплазменным методом Работа силы
Работа силы Школа №625 11 класс Н.М.Турлакова
Школа №625 11 класс Н.М.Турлакова Электризация тел
Электризация тел Надежность
Надежность Необычные барометры
Необычные барометры Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Применение ядерного оружия
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Применение ядерного оружия Поглощение энергии при испарении жидкости и выделение её при конденсации пара
Поглощение энергии при испарении жидкости и выделение её при конденсации пара Звёздный час. Игра по физике
Звёздный час. Игра по физике Проектирование образовательного процесса направленного на формирование ключевых компетенций у учащихся непрофильных классов
Проектирование образовательного процесса направленного на формирование ключевых компетенций у учащихся непрофильных классов Простые механизмы
Простые механизмы Импульс тела (количество движения)
Импульс тела (количество движения) Мощность. Механическая работа
Мощность. Механическая работа Методы исследование структуры. Часть 1
Методы исследование структуры. Часть 1 Общий порядок построения эпюр Qx и Мх
Общий порядок построения эпюр Qx и Мх Презентация на тему Мощность
Презентация на тему Мощность  Инженер древности Герон Александрийский
Инженер древности Герон Александрийский Методы инструментального выявления недостоверного учета электрической энергии
Методы инструментального выявления недостоверного учета электрической энергии Динамика материальной точки
Динамика материальной точки Строительство и эксплуатация зданий и сооружений. Связи и их реакции
Строительство и эксплуатация зданий и сооружений. Связи и их реакции Использование электромагнитов
Использование электромагнитов Виртуальный эксперимент на уроках физики
Виртуальный эксперимент на уроках физики Качественный и количественный характеристики измеряемых величин
Качественный и количественный характеристики измеряемых величин Фрактальная размерность проводников и полупроводников
Фрактальная размерность проводников и полупроводников