Плоская система сходящихся сил

Сдержание
Определение равнодействующей системы сходящих сил методом проекции.
Аналитическое условие.
Проекция силы на две оси.
Определение равнодействующей системы сходящих сил.
Аналитическая форма условия равновесия.
Домашнее задание.

Определение равнодействующей системы сходящихся сил методом проекций.
Аналитическое условие равновесия
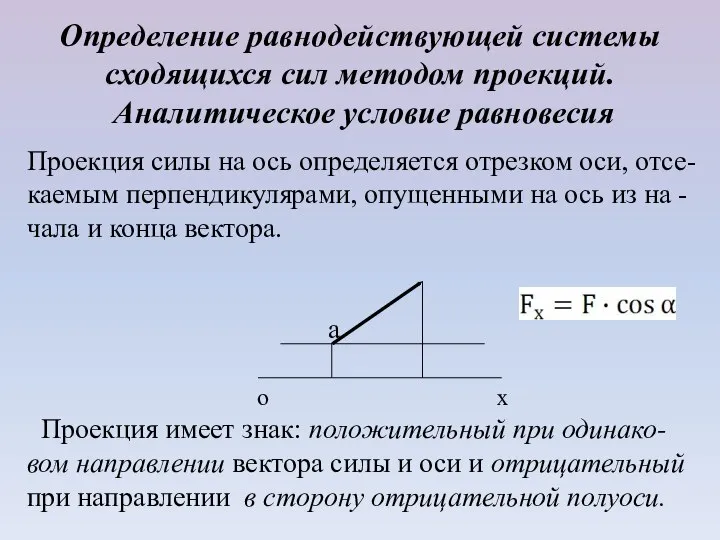
Проекция силы на ось определяется отрезком оси, отсе-
каемым перпендикулярами, опущенными на ось из на -
чала и конца вектора.
а
о х
Проекция имеет знак: положительный при одинако-
вом направлении вектора силы и оси и отрицательный
при направлении в сторону отрицательной полуоси.

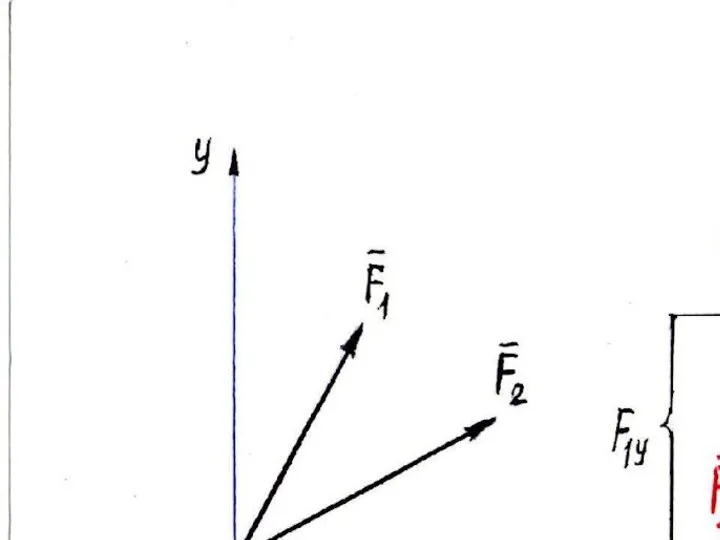
ПРОЕКЦИЯ СИЛЫ НА ДВЕ ОСИ
Если F образует с положи-
тельным направлением
осей х и у соответственно
углы:
По заданным проекциям силы на оси можно опреде-
лить сам вектор силы (её модуль и направление).

Допустим, проекции и силы известны, тогда из
Δ АВС видно, что модуль силы
Чтобы найти углы и , опре-
деляем сначала значения:
,
Затем с помощью таблиц или калькулятора нахо-
дим и
Определение углов и удобнее находить
их:
и

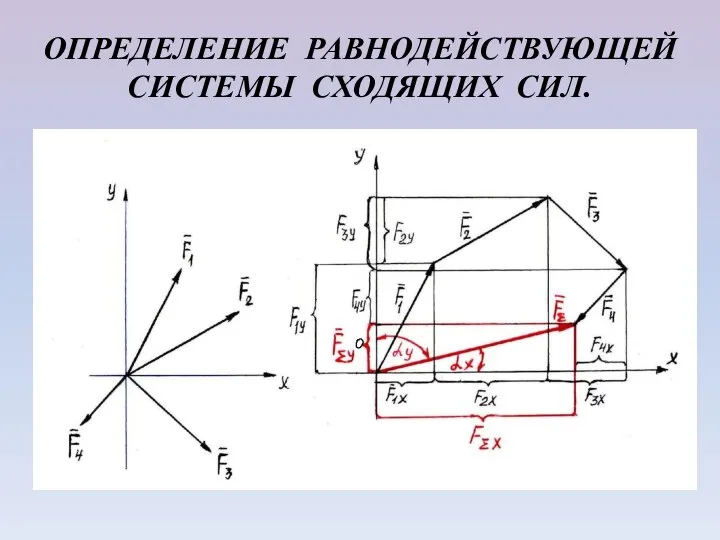
ОПРЕДЕЛЕНИЕ РАВНОДЕЙСТВУЮЩЕЙ СИСТЕМЫ СХОДЯЩИХ СИЛ.

Модуль равнодействующей можно найти по известным
проекциям:
или
Направление вектора равнодействующей можно опре-
делить по величинам и знакам косинусов углов, образу-
емых равнодействующей с осями координат:
Проекция равнодействующей системы сходящих сил на
каждую из осей координат = алгебраической сумме
проекций соответствующих сил на ту же ось.

АНАЛИТИЧЕСКАЯ ФОРМА УСЛОВИЯ РАВНОВЕСИЯ
Исходя из того, что равнодействующая уравнове-
шенной системы сходящихся сил , то её про-
екции на оси: и => равенство
Условие равновесия в аналитической форме:
плоская система сходящих сил находится в равновесии,
если алгебраическая сумма проекций всех сил системы
на любую ось равна нулю:

ДОМАШНЕЕ ЗАДАНИЕ
1. А.И. Аркуша ,, Техническая механика”
стр. 28 – 34
2. Лекции.