Содержание
- 2. Дифракция света Часть 2 Дифракция Фраунгофера на одномерной дифракционной решетке Характеристики дифракционной решетки как спектрального аппарата
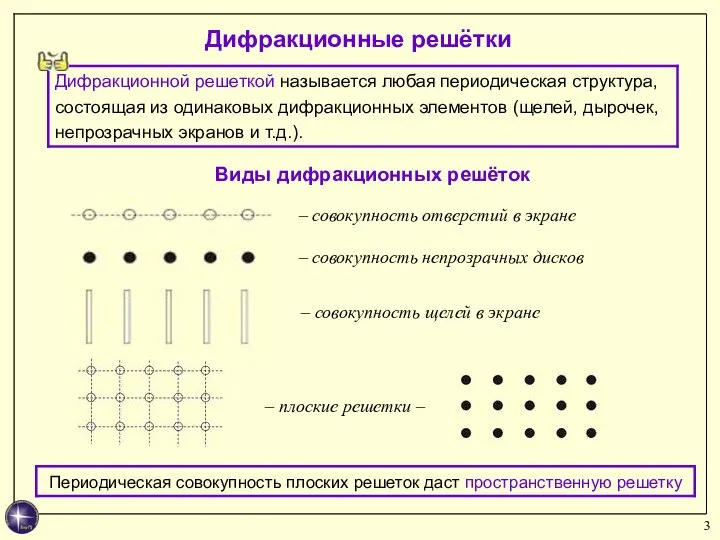
- 3. Дифракционные решётки Виды дифракционных решёток – совокупность отверстий в экране – совокупность непрозрачных дисков – совокупность
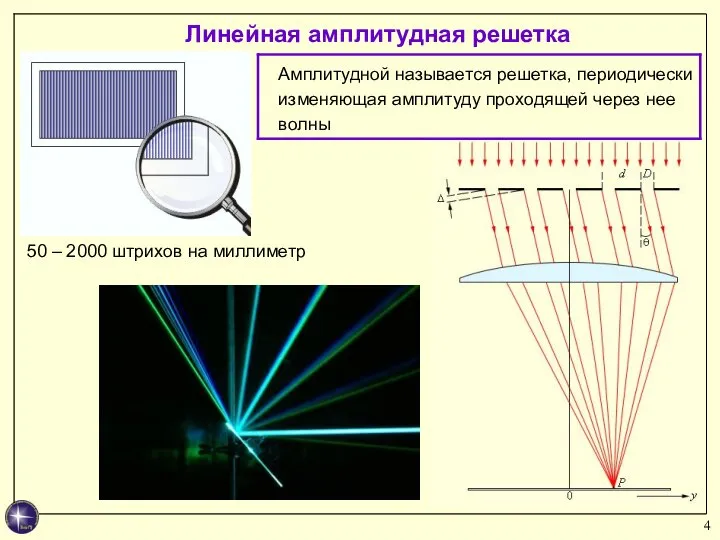
- 4. Линейная амплитудная решетка 50 – 2000 штрихов на миллиметр
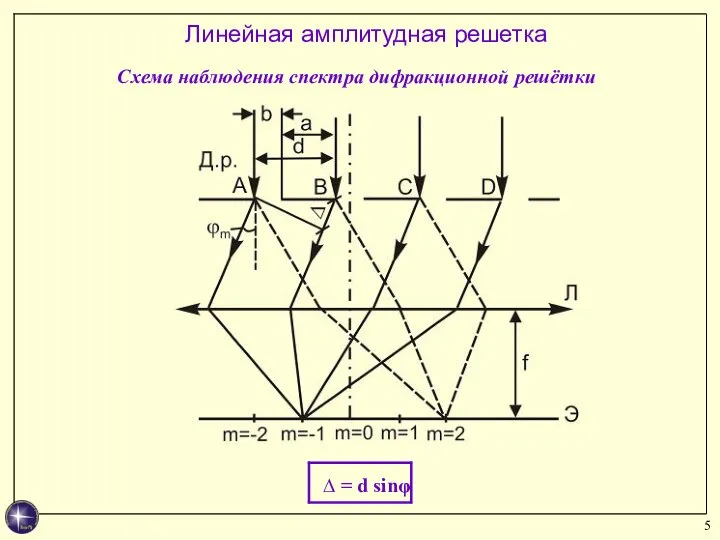
- 5. Линейная амплитудная решетка Схема наблюдения спектра дифракционной решётки
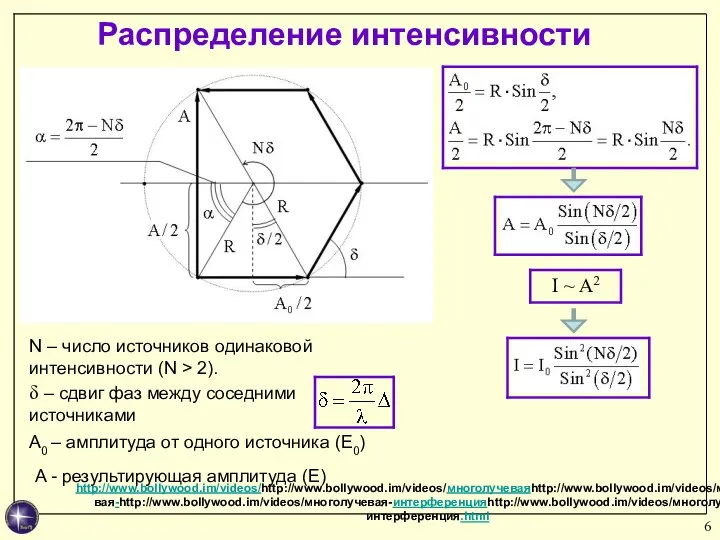
- 6. Распределение интенсивности N – число источников одинаковой интенсивности (N > 2). δ – сдвиг фаз между
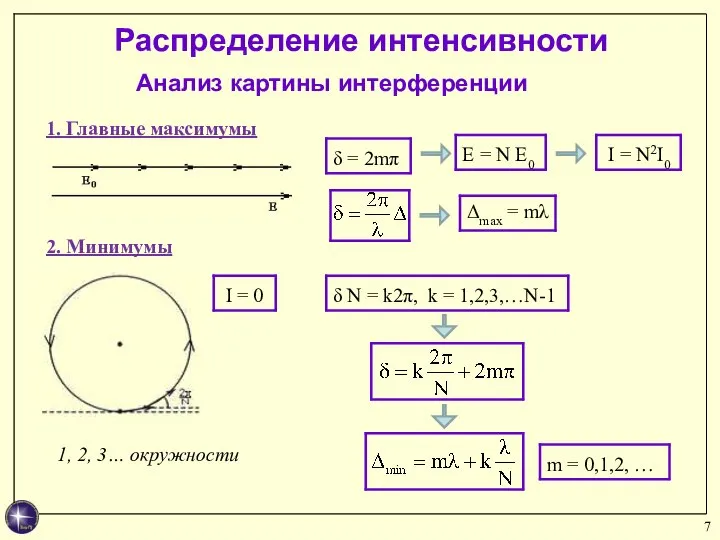
- 7. Распределение интенсивности 1. Главные максимумы Анализ картины интерференции 2. Минимумы Δmax = mλ 1, 2, 3…
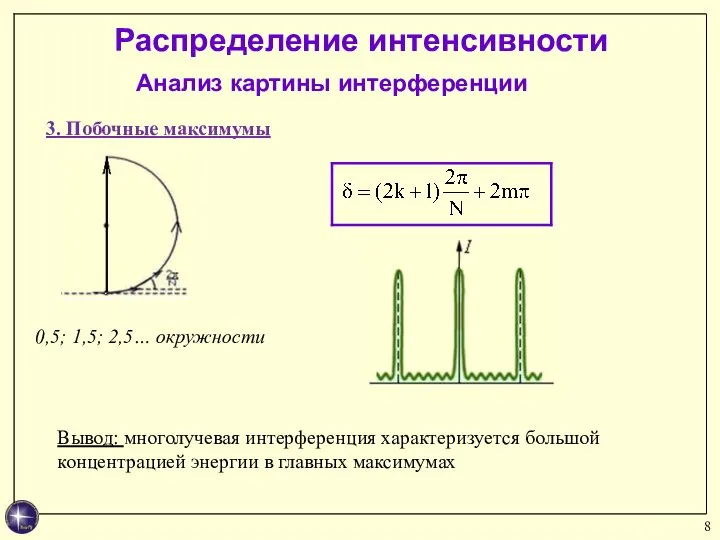
- 8. Распределение интенсивности 3. Побочные максимумы Анализ картины интерференции 0,5; 1,5; 2,5… окружности Вывод: многолучевая интерференция характеризуется
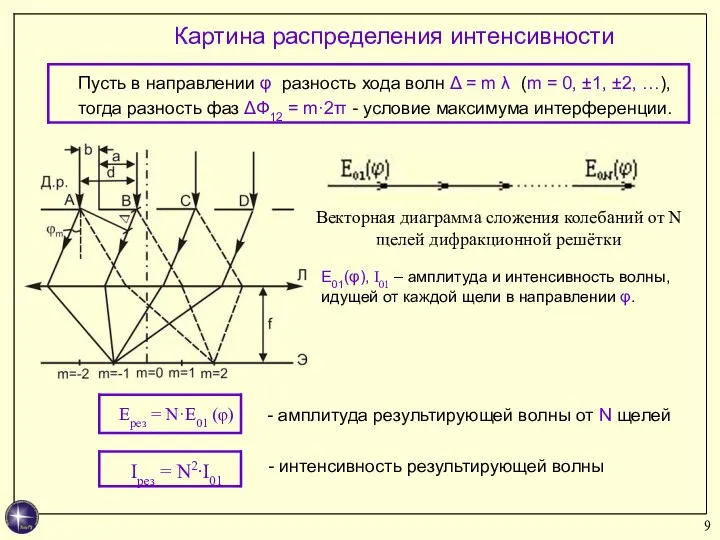
- 9. Картина распределения интенсивности Векторная диаграмма сложения колебаний от N щелей дифракционной решётки - амплитуда результирующей волны
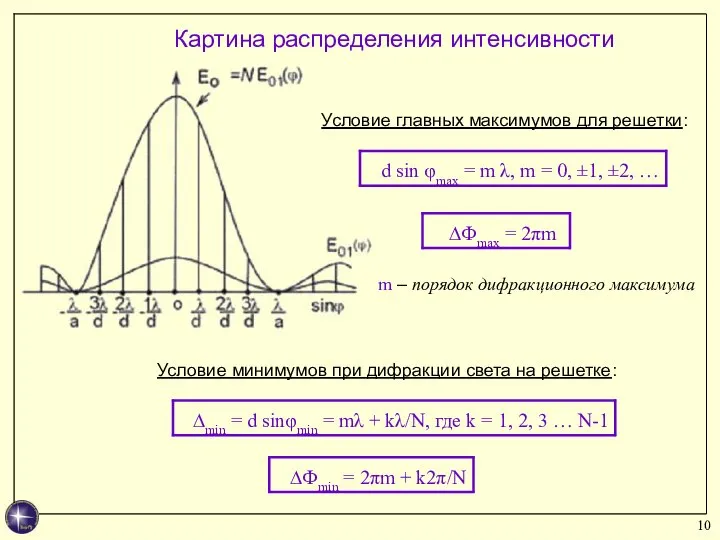
- 10. Условие главных максимумов для решетки: m – порядок дифракционного максимума Картина распределения интенсивности Условие минимумов при
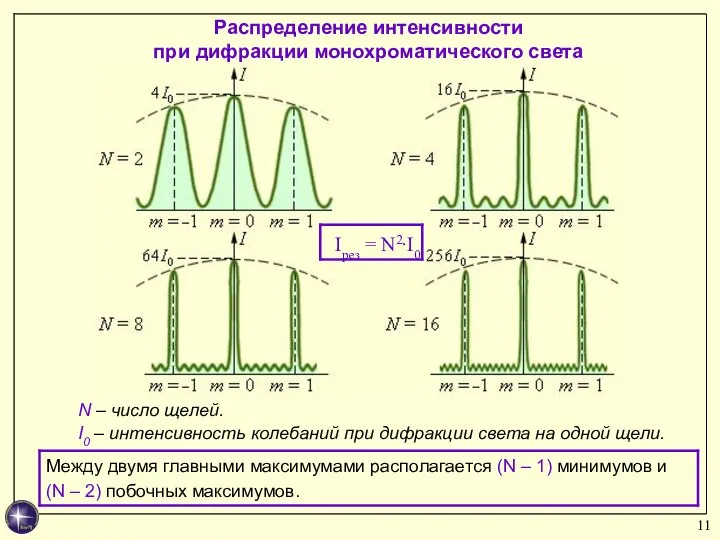
- 11. Распределение интенсивности при дифракции монохроматического света N – число щелей. I0 – интенсивность колебаний при дифракции
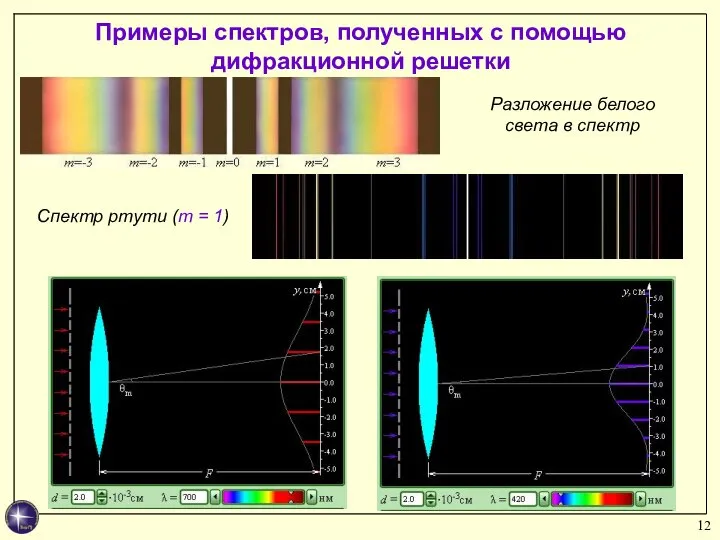
- 12. Примеры спектров, полученных с помощью дифракционной решетки Разложение белого света в спектр Спектр ртути (m =
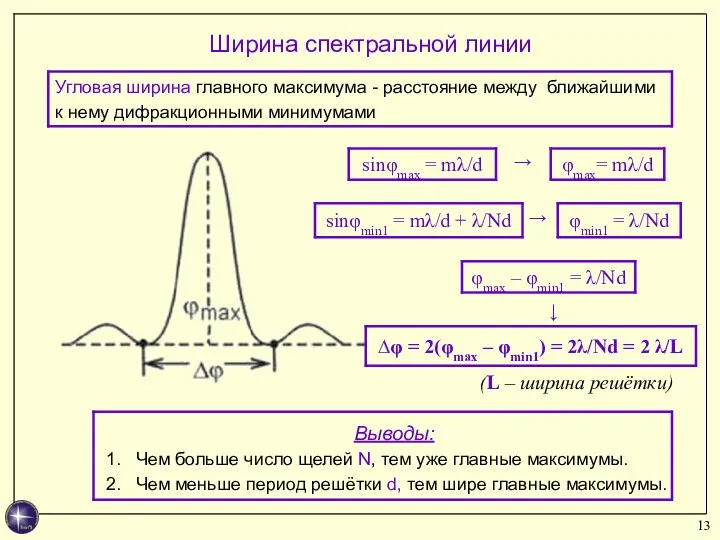
- 13. → (L – ширина решётки) → → Ширина спектральной линии
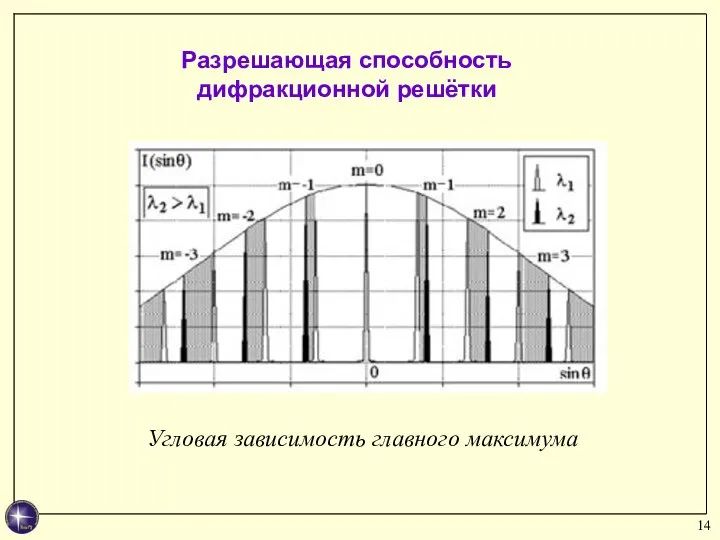
- 14. Разрешающая способность дифракционной решётки Угловая зависимость главного максимума
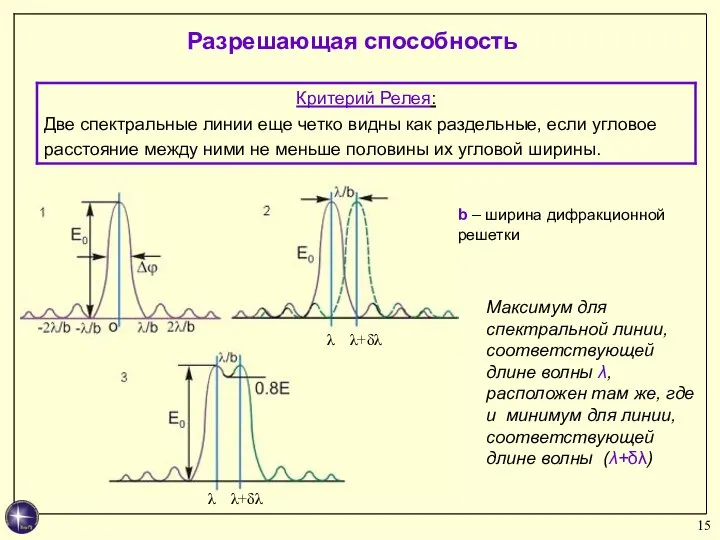
- 15. Максимум для спектральной линии, соответствующей длине волны λ, расположен там же, где и минимум для линии,
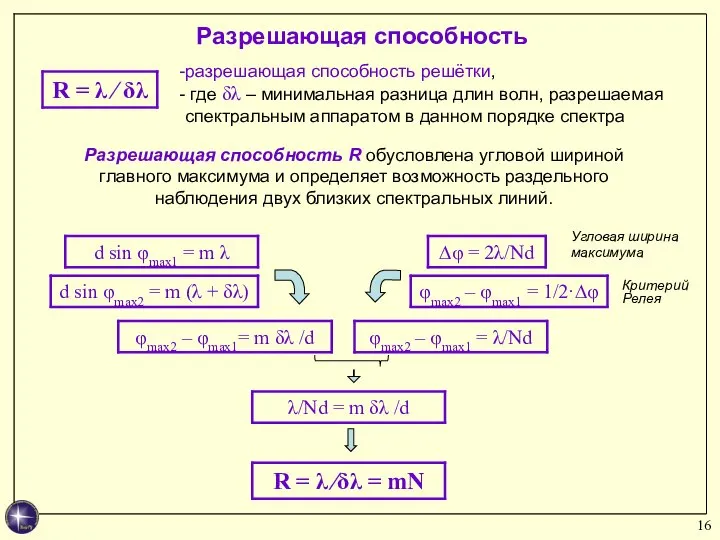
- 16. разрешающая способность решётки, где δλ – минимальная разница длин волн, разрешаемая спектральным аппаратом в данном порядке
- 17. Элементы голографии Физические основы голографической записи изображений Голографирование в плоских волнах Голограмма точки Толстослойные голограммы Свойства
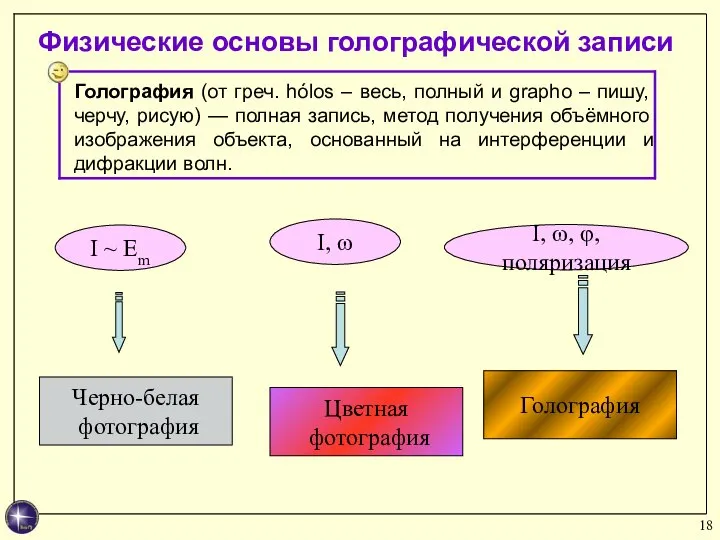
- 18. Физические основы голографической записи I ~ Em Черно-белая фотография I, ω Цветная фотография I, ω, φ,
- 19. В 1962 г. И. Лейт и Ю. Упатниекс получили первые пропускающие голограммы объемных объектов, выполненные с
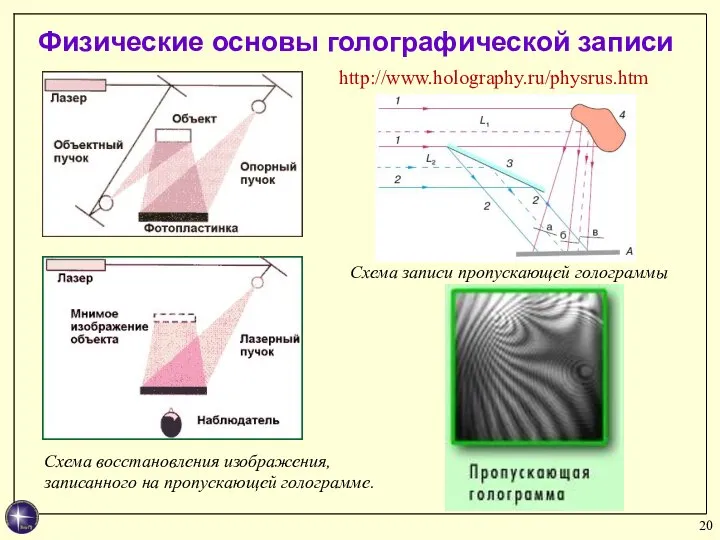
- 20. Физические основы голографической записи Схема восстановления изображения, записанного на пропускающей голограмме. Схема записи пропускающей голограммы http://www.holography.ru/physrus.htm
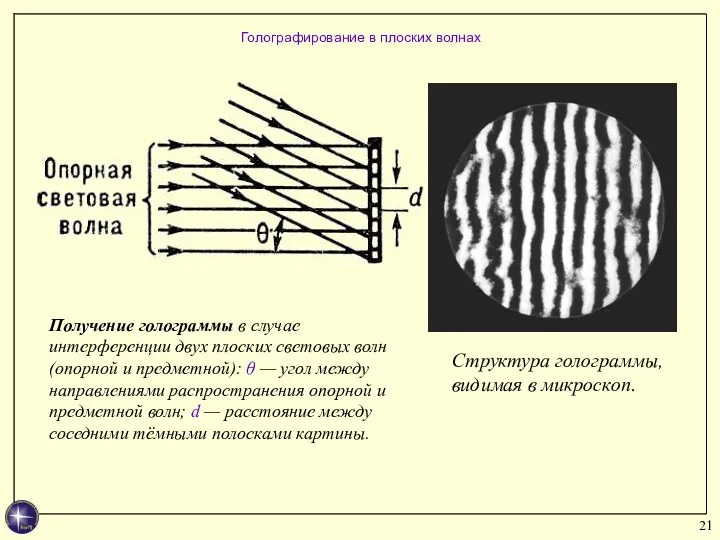
- 21. Голографирование в плоских волнах Получение голограммы в случае интерференции двух плоских световых волн (опорной и предметной):
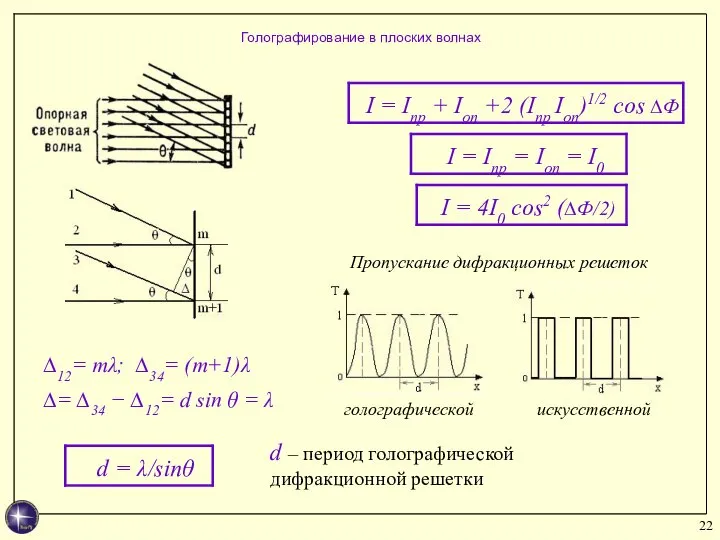
- 22. Голографирование в плоских волнах ∆12= mλ; ∆34= (m+1)λ ∆= ∆34 − ∆12= d sin θ =
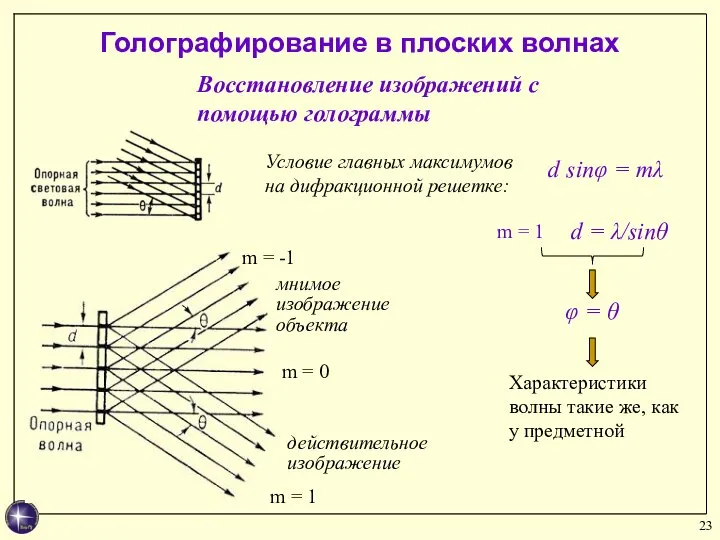
- 23. Голографирование в плоских волнах Восстановление изображений с помощью голограммы мнимое изображение объекта действительное изображение m =
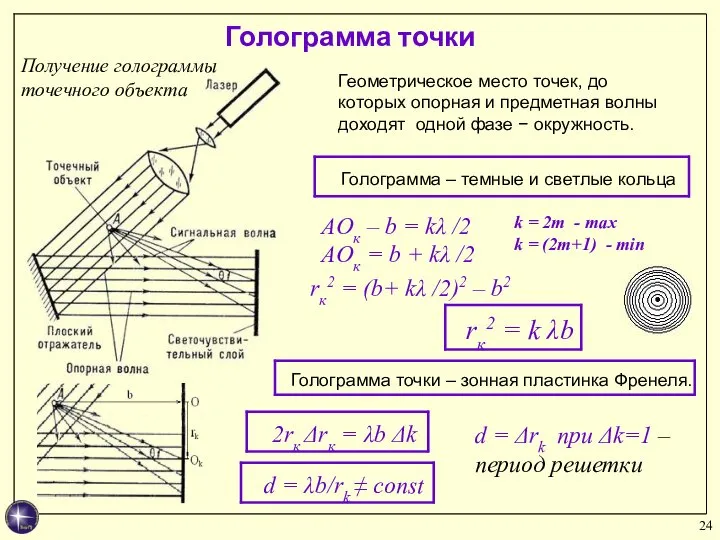
- 24. Голограмма точки Получение голограммы точечного объекта Геометрическое место точек, до которых опорная и предметная волны доходят
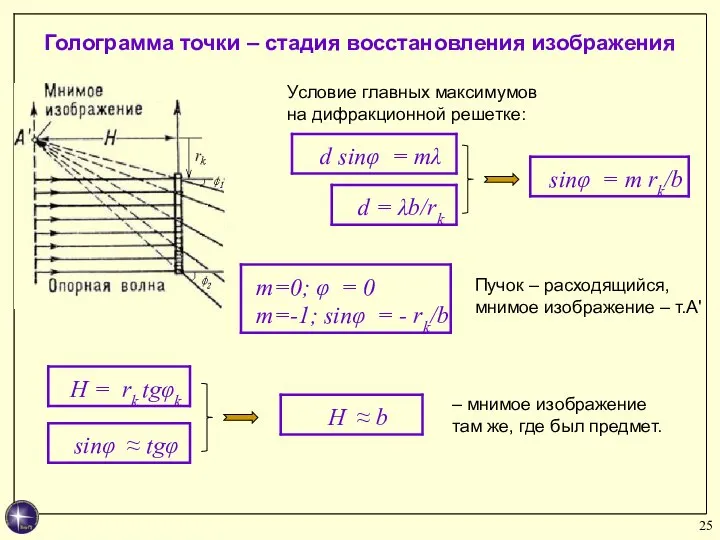
- 25. Голограмма точки – стадия восстановления изображения Условие главных максимумов на дифракционной решетке: Пучок – расходящийся, мнимое
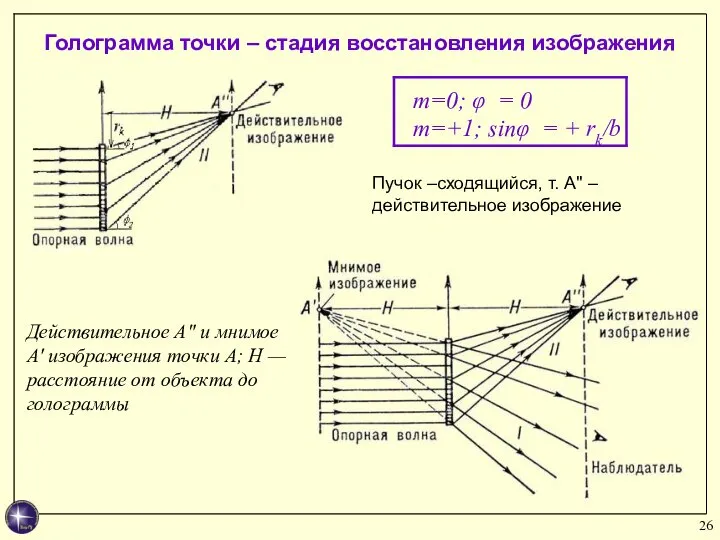
- 26. Голограмма точки – стадия восстановления изображения Действительное А" и мнимое A′ изображения точки А; Н —
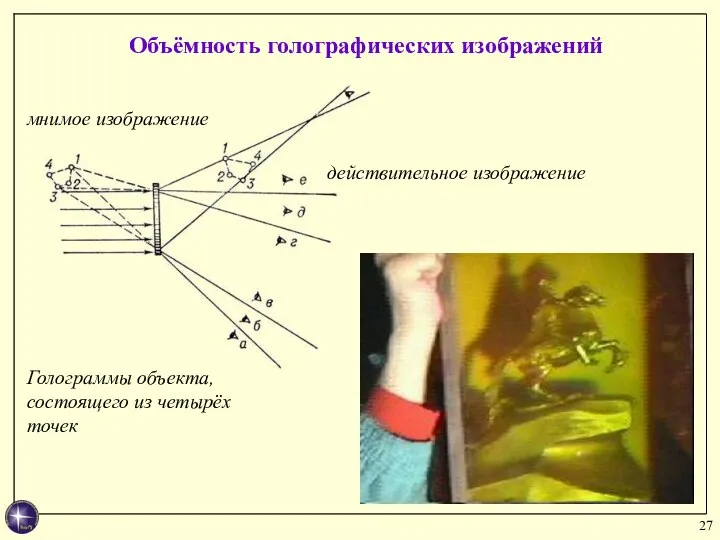
- 27. Голограммы объекта, состоящего из четырёх точек Объёмность голографических изображений действительное изображение мнимое изображение
- 28. Объёмность голографических изображений Фотографии мнимого голографического изображения шахматных фигур, полученные при разных направлениях наблюдения
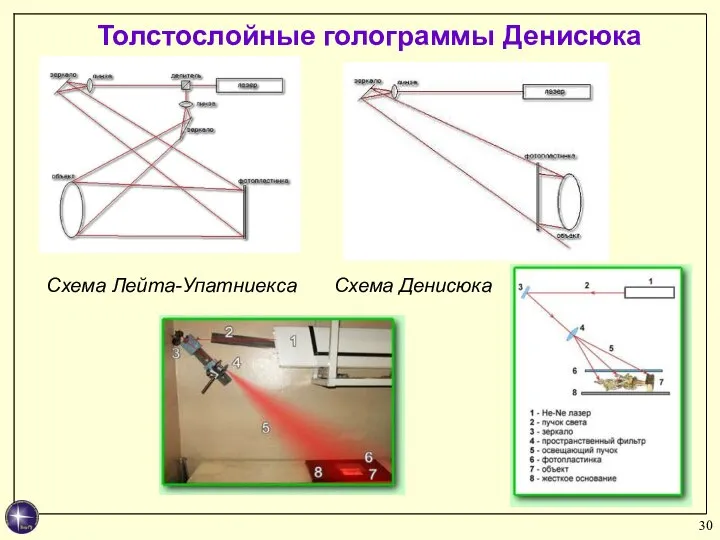
- 30. Толстослойные голограммы Денисюка Схема Лейта-Упатниекса Схема Денисюка
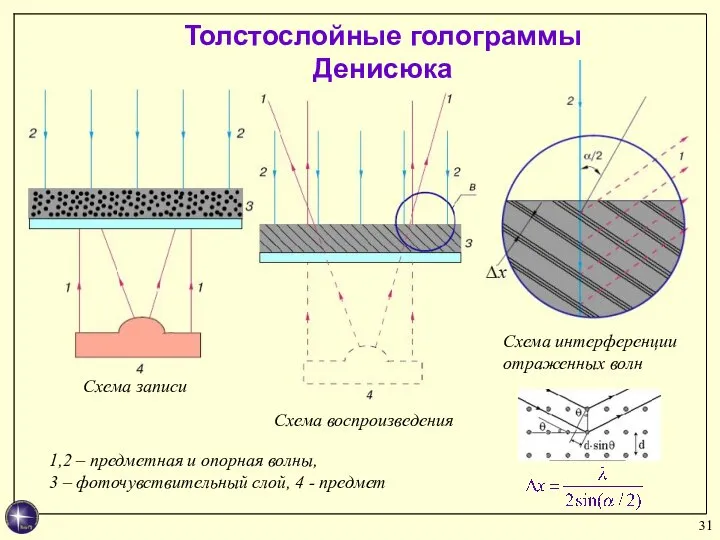
- 31. Толстослойные голограммы Денисюка Cхема записи Cхема воспроизведения Cхема интерференции отраженных волн 1,2 – предметная и опорная
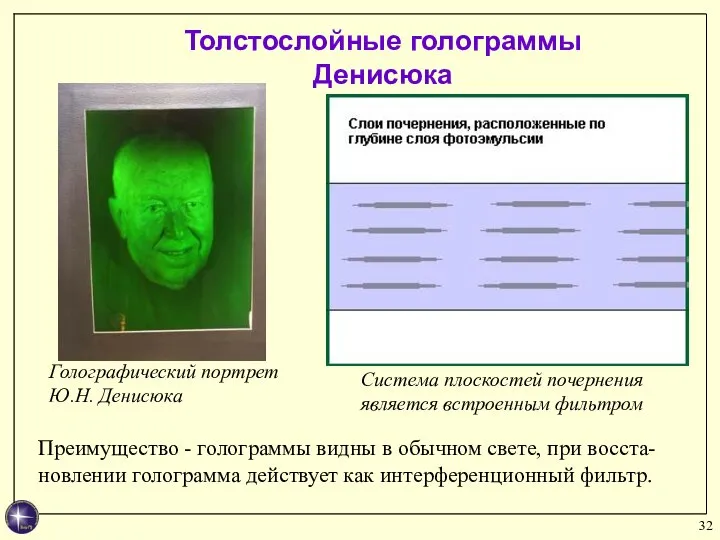
- 32. Толстослойные голограммы Денисюка Система плоскостей почернения является встроенным фильтром Преимущество - голограммы видны в обычном свете,
- 33. Голографическая установка Ю.Н. Денисюка, 1959г., Москва, Политехнический музей Голограммы Денисюка видео
- 34. В 1969 г. Стивен Бентон из Polaroid Research Laboratories (США) изготовил пропускающую голограмму, видимую в обычном
- 35. Свойства голограмм
- 36. При просмотре голограмм можно менять форму волнового фронта опорной волны. Освещая голограмму расходящейся сферической волной, можно
- 37. Применение голографии Музейные выставки, художественная голография Создание объёмного цветного телевидения Создание новых систем памяти с большой
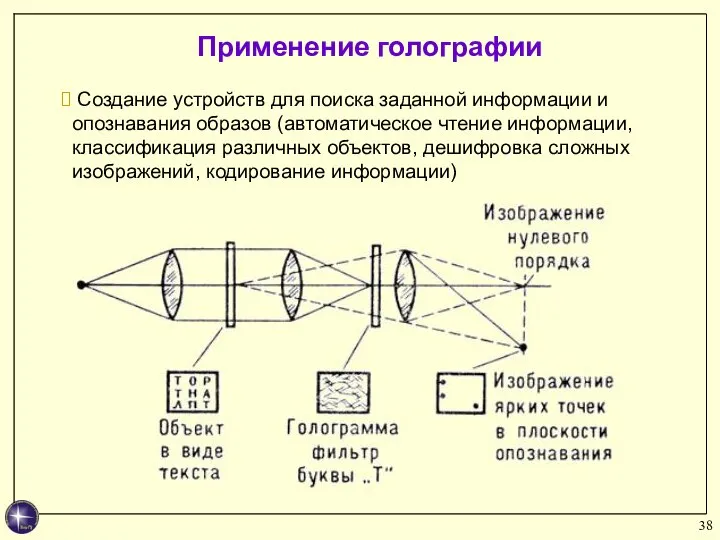
- 38. Создание устройств для поиска заданной информации и опознавания образов (автоматическое чтение информации, классификация различных объектов, дешифровка
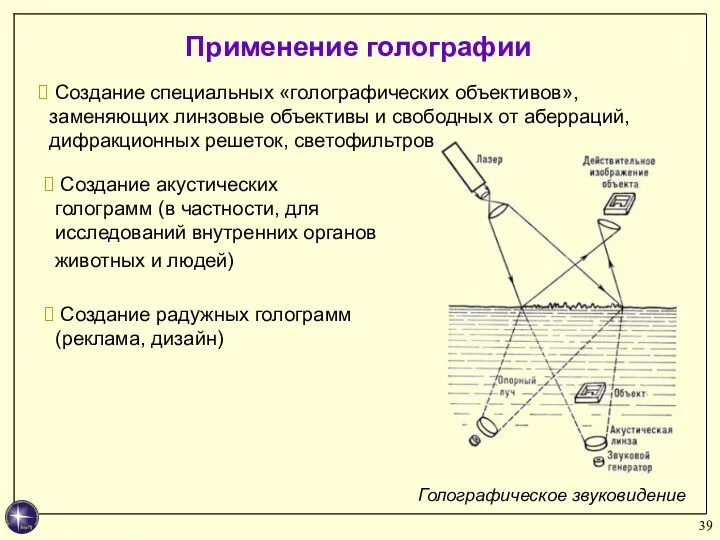
- 39. Применение голографии Создание специальных «голографических объективов», заменяющих линзовые объективы и свободных от аберраций, дифракционных решеток, светофильтров
- 40. Голографическая 3D-карта местности Компания Zebra Imaging производит удивительные голографические 3D-карты местности, и поверьте, технология эта куда
- 42. Скачать презентацию











 Основы электродинамики. Электрическое поле
Основы электродинамики. Электрическое поле Диод Шоттки
Диод Шоттки Электромагнитные колебания и волны
Электромагнитные колебания и волны Спектроскоп. Виды спектров
Спектроскоп. Виды спектров Давление. Единицы давления
Давление. Единицы давления Задачи для курсовой работы
Задачи для курсовой работы Неньютоновская жидкость
Неньютоновская жидкость Електричні двигуни
Електричні двигуни Updated_Строение атома
Updated_Строение атома Физика на службе человека
Физика на службе человека Частицы
Частицы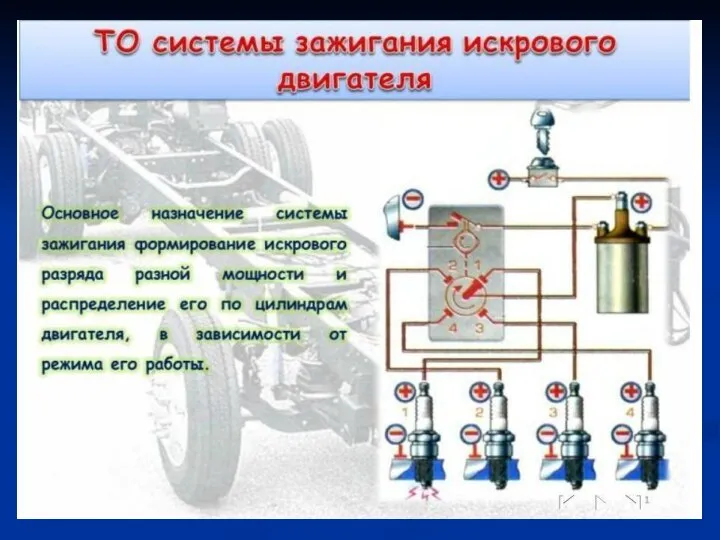 ТО системы зажигания искрового двигателя
ТО системы зажигания искрового двигателя Томас Юнг
Томас Юнг Поверхностные и пространственные методы визуализации потока в аэродинамических трубах
Поверхностные и пространственные методы визуализации потока в аэродинамических трубах Виды радиоактивного излучения. (Лекция 3)
Виды радиоактивного излучения. (Лекция 3) Изучение устройства радиоприёмника
Изучение устройства радиоприёмника Прозрачный люминесцентный солнечный концентратор
Прозрачный люминесцентный солнечный концентратор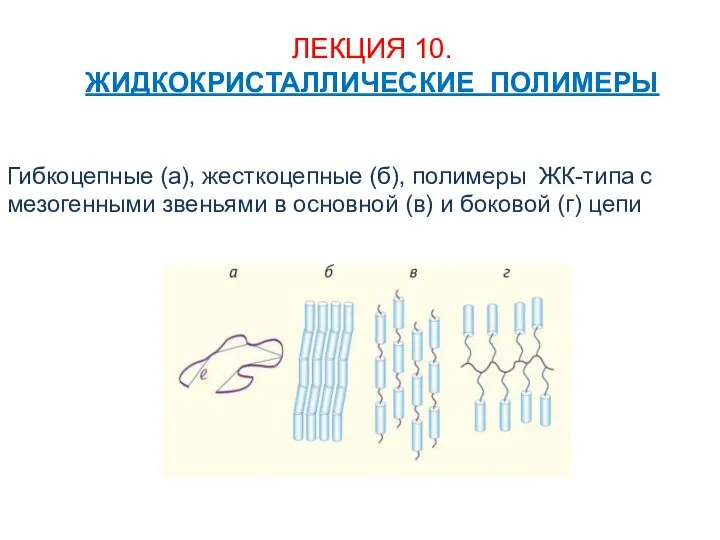 Жидкокристаллические полимеры
Жидкокристаллические полимеры Электромагнитная индукция
Электромагнитная индукция Движение и взаимодействие тел. Повторительно-обобщающий урок-игра
Движение и взаимодействие тел. Повторительно-обобщающий урок-игра Делимость электрического заряда. Строение атома
Делимость электрического заряда. Строение атома Нанороботы в биомедицине
Нанороботы в биомедицине Что изучает физика
Что изучает физика Электрические методы контроля
Электрические методы контроля Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Прибор, открывающий тайны
Прибор, открывающий тайны Досліди Фарадея. Явище електромагнітної індукції. 9кл
Досліди Фарадея. Явище електромагнітної індукції. 9кл Никола Тесла. Человек, обогнавший своё время
Никола Тесла. Человек, обогнавший своё время