Математический и пружинный маятники

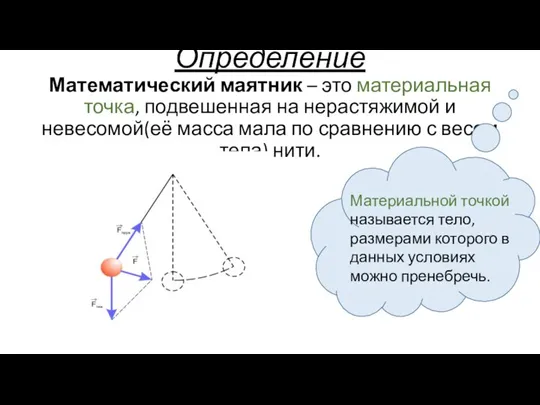
Определение
Математический маятник – это материальная точка, подвешенная на нерастяжимой и невесомой(её масса мала по сравнению с весом тела) нити.
Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.

Зависимость Математического маятника
Галилео Галилей
(1564-1642гг.)
Великий итальянский ученый – один из создателей точного естествознания.
Учился сначала в монастырской школе, а затем в университете. Уже в студенческие годы Галилей увлекся изучением колебаний. Он обнаружил, что колебания маятника не зависят от его массы, а определяются длиной подвеса.

ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКОГО МАЯТНИКА
Период (T):
Христиа́н Гю́йгенс
g - Ускорение свободного падения(м/с2)
- Длина маятника(м)
(1629-1695гг.)

ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКОГО МАЯТНИКА
Период (T):
Христиа́н Гю́йгенс
g - Ускорение свободного падения(м/с2)
- Длина маятника(м)
(1629-1695гг.)

ДА ЗДРАВСТВУЕТ ТОЧНОЕ ВРЕМЯ !

Характеристика Математического маятника
Циклическая частота:

Характеристика Математического маятника
Циклическая частота:

График устанавливает зависимость смещения тела со временем.

Пружинный маятник.
Маятник на пружине — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Характеристика Пружинных маятников
Закон Гука:
Сила упругости пропорциональна смещению тела (удлинению пружины):
Fупр = –kx.
k – коэффициент жесткости пружины.
x – отклонение груза от точки равновесия

Характеристика Пружинного маятника
Груз на пружине называют линейным гармоническим осциллятором.

Характеристика Пружинного маятника
Собственная частота ( ω0 )
Период
(Т)
k – коэффициент жесткости пружины.
m – масса маятника.
k – коэффициент жесткости пружины.
m – масса маятника.
- математическая постоянная ≈ 3,14

Задачи
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла v ?

Задачи
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла ?
Ответ:

Задача
Пример . Тело массой m=2 кг подвешено к упругой пружине, совершает гармонические колебания. Определите жёсткость k пружины, если за время t=1,5мин число N полных колебаний равно 60.
Дано: m=2кг; t=1,5мин=90с; N=60.
Найти: k.

Решение: Период гармонических колебаний тела, подвешенного на пружине (пружинный маятник),
где m- масса тела; k- жёсткость пружины.
С другой стороны, период колебаний
где t – время, за которое совершается N полных колебаний.
Приравняв оба выражения
Найдём искомую жёсткость пружины
Ответ: k=35,1 Н/м.