с неподвижной опорой. Ось шарнира перпендикулярна плоскости качаний маятника (плоскости чертежа). Введем обозначения: l — длина маятника (l = OB), M — его масса, J — его момент инерции относительно шарнира O. Маятник представляет собой однородный стержень, поэтому его центр масс расположен в середине отрезка OB и J = Ml^2/3. Угол отклонения маятника от вертикали обозначается через φ или ψ.
Симметричный относительно своей оси вращения маховик смонтирован на маятнике так, что его центр расположен в конце маятника OB – в точке B. Здесь маховик изображен в виде окружности с центром в точке B. Маховик может поворачиваться в ту или иную сторону вокруг про6 ходящей через точку B горизонтальной оси, перпендикулярной плоскости качаний маятника (плоскости чертежа). Эта ось параллельна оси шарнира O. Ось вращения маховика является продолжением оси ротора электродвигателя. Таким образом, маховик вместе с якорем двигателя имеет по отношению к маятнику одну степень свободы. Вся система имеет две степени свободы. Единственный управляющий параметр в системе – напряжение u, подаваемое на электродвигатель, который вращает маховик.
















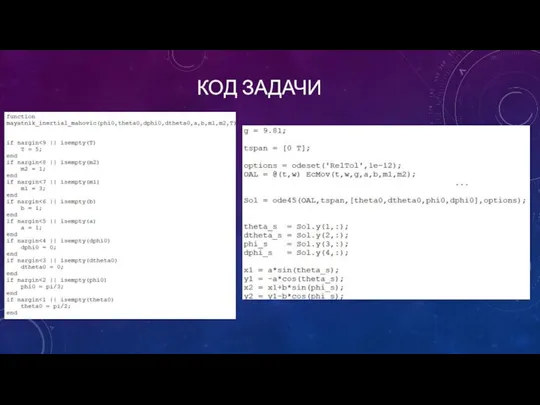
 0008959c-88e65e04
0008959c-88e65e04 Презентация на тему Калейдоскоп физических явлений
Презентация на тему Калейдоскоп физических явлений  Ускорение. Движение с постоянным ускорением. Уравнение движения. (10 класс)
Ускорение. Движение с постоянным ускорением. Уравнение движения. (10 класс) Сила упругости
Сила упругости Классификация томографов и магнитов
Классификация томографов и магнитов Проблемы применения нанотехнологии
Проблемы применения нанотехнологии Презентация на тему Импульс Закон сохранения импульса
Презентация на тему Импульс Закон сохранения импульса  Электрический ток в металлах
Электрический ток в металлах Презентация на тему Принцип относительности в механике. Постулаты теории относительности (11 класс)
Презентация на тему Принцип относительности в механике. Постулаты теории относительности (11 класс)  Христиан Гюйгенс вклад в развитие механики
Христиан Гюйгенс вклад в развитие механики Простые механизмы. Рычаг. Правило равновесия рычага
Простые механизмы. Рычаг. Правило равновесия рычага Электрические машины. Законы электромеханики
Электрические машины. Законы электромеханики Электромагнетизм
Электромагнетизм Газораспределительный механизм
Газораспределительный механизм Магнитное поле Земли
Магнитное поле Земли Работа, мощность силы. Кинетическая энергия. Лекция 9
Работа, мощность силы. Кинетическая энергия. Лекция 9 Электрические колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях
Электрические колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях Закон Ома для участка электрической цепи
Закон Ома для участка электрической цепи Разработка и моделирование МЭМС-датчика давления воздушной среды
Разработка и моделирование МЭМС-датчика давления воздушной среды Периодическое движение
Периодическое движение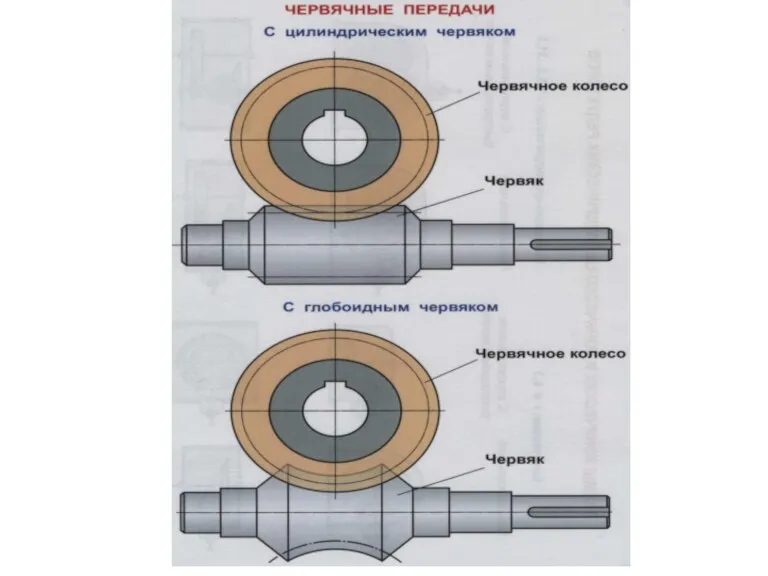 Червячные передачи
Червячные передачи Теория линейных электрических цепей
Теория линейных электрических цепей Исследование зависимостей термодинамических величин
Исследование зависимостей термодинамических величин Транзисторы. Практическое применение транзисторов, диодов и конденсаторов. Лекция 6
Транзисторы. Практическое применение транзисторов, диодов и конденсаторов. Лекция 6 Поршневые компрессоры
Поршневые компрессоры Гуманитарная направленность преподавания физики при организации самостоятельной работы студентов
Гуманитарная направленность преподавания физики при организации самостоятельной работы студентов Вопросы для аттестации. Квантовая теория
Вопросы для аттестации. Квантовая теория Презентация на тему Атом
Презентация на тему Атом