Механические колебания и волны

План лекции
Свободные незатухающие гармонические колебания:
Пружинный маятник
Математический маятник
Крутильный маятник
Физический маятник
Затухающие колебания с вязким трением.
Вынужденные колебания. Резонанс.
Параметрический резонанс.
Решение задач
Волны в упругих средах

Демонстрации
Автоколебания
Резонанс камертонов
Параметрический резонанс
Маятник Капицы
Волна в массивной пружине

Колебательные процессы
Колебание – изменение состояния системы по периодическому или почти периодическому закону: маятник часов, груз на пружине, гитарная струна, давление воздуха в звуковой волне.
Свободные (или собственные) колебания: колебания в системе, предоставленной самой себе:
шарик в лунке, груз на нити.
Вынужденные колебания – колебания под действием внешней периодической силы: вибрации моста, качели.
Автоколебания, параметрические колебания (часы, качели)

Свободные незатухающие
гармонические колебания.
Пружинный маятник
mx” = - kx ⇨ mx” + kx = 0 ⇨
x” + ω02x = 0 – дифференциальное уравнение гармонических колебаний (ω02 = k/m)
x = Acos(ω0t + φ0) – гармоническое колебание
A – амплитуда колебаний
ω0 – циклическая частота
φ0 – начальная фаза
ω0t + φ0 – фаза колебаний
T = 2π/ ω0 – период колебаний
Изохронность: ω0, Т – определяются только свойствами системы и не зависит от амплитуды.
F = -kx – квазиупругая возвращающая сила

Скорость и ускорение при гармонических колебаниях
Смещение:
x = Acos(ω0t + φ0)
Скорость:
v = x’ = - ω0Asin(ω0t + φ0) = ω0Acos(ω0t + φ0 + π/2);
v0 = ω0A – амплитуда скорости;
скорость опережает смещение x по фазе на π/2.
Ускорение
a = - ω02Acos(ω0t + φ0) = ω02Acos(ω0t + φ0 + π)
a0 = ω02A – амплитуда ускорения;
ускорение в противофазе со смещением

Векторная диаграмма
Векторная диаграмма:
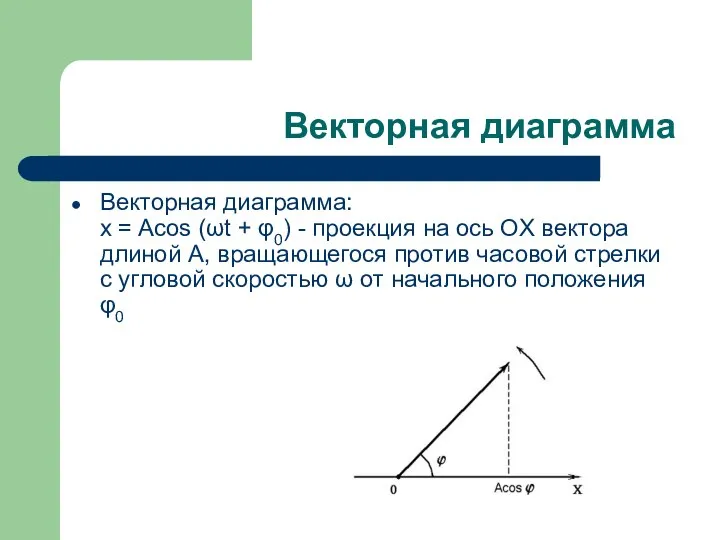
x = Acos (ωt + φ0) - проекция на ось OX вектора длиной A, вращающегося против часовой стрелки с угловой скоростью ω от начального положения φ0

Векторная диаграмма гармонических колебаний (картинка)
Смещение: x = Acos(ω0t + φ0)
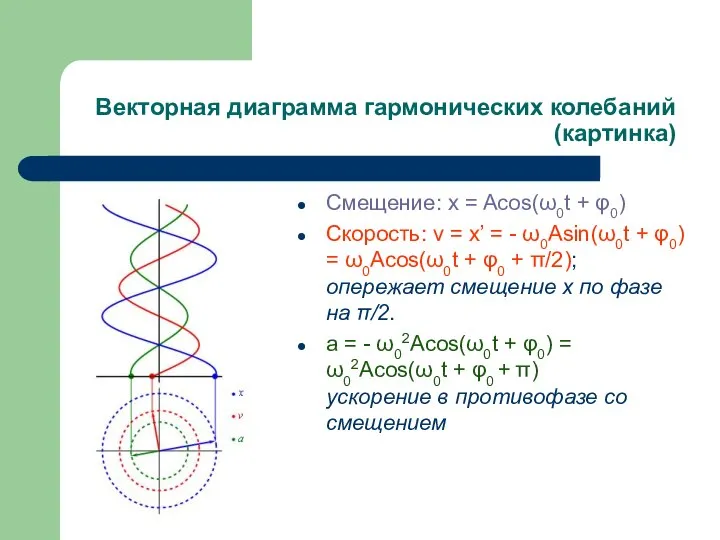
Скорость: v = x’ = - ω0Asin(ω0t + φ0) = ω0Acos(ω0t + φ0 + π/2);
опережает смещение x по фазе на π/2.
a = - ω02Acos(ω0t + φ0) = ω02Acos(ω0t + φ0 + π)
ускорение в противофазе со смещением

Энергия гармонических колебаний
Потенциальная энергия:
П = kx2/2 = ½kA2cos2(ω0t + φ0)
Кинетическая энергия:
K = mv2/2 = ½mω02A2sin2(ω0t + φ0) =
½кA2sin2(ω0t + φ0)
Полная энергия:
Е = П + K = const = ½kA2 = ½mv02
Для гармонических колебаний:
= <П> = ½E

Задача 10.1
Фазовая траектория – эллипс:
x2/A2 + v2/v02 = 1
Задача 10.1. Нарисуйте характерный график зависимости координаты x тела, совершающего гармонические колебания без затухания от его скорости x’ (фазовая траектория) для нескольких значений энергии системы. То же самое для осциллятора с затуханием.
Решение:
x = Acosωt; v = x’ = -ωAsinωt → kx2/2 + mx’2/2 = E →
x2/(2E/k) + x’2/(2E/m) = 1 – эллипс с п/осями a = (2E/k)1/2 ; b = (2E/m)1/2
Затухание A(t) = A0e-γt ; 2γ = β/m; β – коэффициент вязкого трения: fтр = -βv

Период колебаний: энергетический метод для колебательных систем с одной степенью свободы
q – обобщённая координата (смещение, угол поворота, заряд на конденсаторе)
q’ – обобщённая скорость (скорость смещения, угловая скорость, электрический ток)
Уравнение энергии: ½ αq2 +½ βq’2 = const
П = ½ αq2 – потенциальная энергия
K = ½ βq’2 – кинетическая энергия
ω2 = α/β – циклическая частота α – эффективная жёсткость системы
β – инерционность системы

Математический маятник
Математический маятник – материальная точка на нерастяжимой лёгкой нити в поле тяжести Земли.
Энергетический метод:
θ – угол отклонения нити от вертикали (обобщённая координата).
Потенциальная энергия:
П = mgL(1 – cosθ) ≈ ½ mgLθ2 = ½ кθ2
k = mgL – эффективная жёсткость
Кинетическая энергия:
K = ½ m(Lθ’)2 = ½ mL2 θ’2 = ½ μθ’2 μ = mL2 – инерционность системы
Уравнение колебаний: ½кθ2 + ½ μθ’2 = const
ω02 = к/μ = g/L; T = 2π/ω0 = 2π(L/g)1/2

Задача 10.5
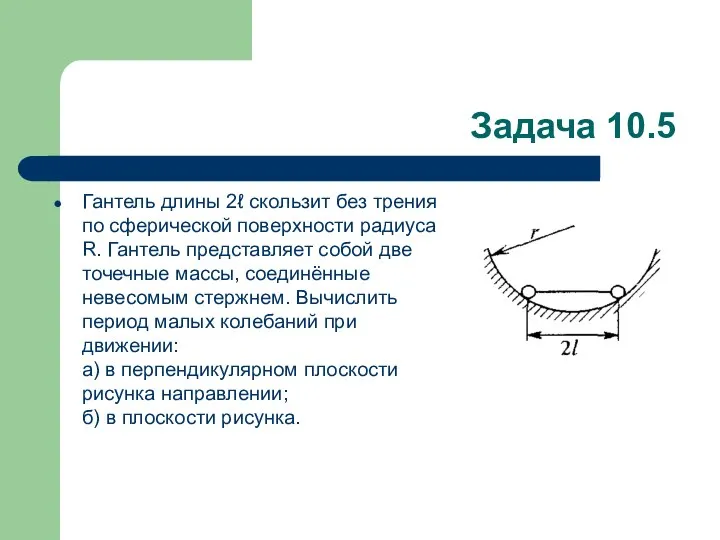
Гантель длины 2ℓ скользит без трения по сферической поверхности радиуса R. Гантель представляет собой две точечные массы, соединённые невесомым стержнем. Вычислить период малых колебаний при движении:
а) в перпендикулярном плоскости рисунка направлении;
б) в плоскости рисунка.

Решение
Решение:
b) П = 2mgr(1 – cosα) = ½ (2mgrφ2) = ½(2mgφ2(R2 - ℓ2)1/2;
K = 2mR2φ’2/2 → жёсткость α = 2mg(R2 - ℓ2)1/2; инерционность β = 2mR2 →
ω2 = α/β = g(R2 - ℓ2)1/2/R2 //ответ
a) r = (R2 - ℓ2)1/2 →
потенциальная энергия: П = ½ (2mgrφ2) → жёсткость α = 2mgr;
кинетическая энергия K = ½ (2mr2φ’2) →
инерционность β = 2mr2 →
ω02 = α/β = g/r = g/(R2 - ℓ2)1/2 //ответ

Крутильный маятник

Крутильные колебания
Диск на упругой нити:
Момент упругих сил Mz = - kθ, k – коэффициент “крутильной” жёсткости
I0θ” = - kθ ⇨ θ” + (k/I0)θ = 0 ⇨ ω02 = k/I0

Физический маятник
Физический маятник - твёрдое тело, совершающее колебания вокруг неподвижной горизонтальной оси.
Энергетический метод:
Потенциальная энергия:
П = mga(1 – cosθ) ≈ ½ mgaθ2
Кинетическая энергия:
K = ½Iθ’2, I = Ic + ma2 - момент инерции относительно оси O
Уравнение колебаний: ½mgaθ2 + ½ Iθ’2 = const
ω02 = mga/I; T = 2π/ω0 = 2π(l/mga)1/2

Приведённая длина. Центр качания. Теорема Гюйгенса.
Оборотный маятник и измерение g
Lпр = I/ma – длина математического маятника с тем же периодом колебаний
Lпр = I/ma = (Ic + ma2)/ma = a + Ic/ma
Центр качания О’ расположен на прямой ОС расстоянии Lпр от точки подвеса O
Теорема Гюйгенса
Точка подвеса и центр качания являются “сопряжёнными” точками: если маятник подвесить за центр качания, то его период не изменится.
Доказательство: Lпр = a + Ic/ma ⇨ a2 - Lпрa + Ic/m = 0 ⇨
a1 + a2 = Lпр
Оборотный маятник и измерение g: экспериментально определяют расстояние между сопряжёнными точками ОО’ = Lпр и рассчитывают g по формуле: g = Lпрω02

Задача 10.3
10.3. Найти период колебаний однородного стержня длины ℓ = 50 см, если ось вращения проходит через точку, находящуюся на расстоянии d = 10 см от его верхнего конца.
Решение:
a = ½ℓ - d = 15 см
T = 2π(I/ma)1/2 = 2π((Iс + ma2) /mag)1/2=
2π((Iс/ma + a)/g)1/2 →
ℓпр = Iс/ma + a = ℓ2/12a + a ≈ 14 + 15 = 29 см. →
T = 2π(ℓпр/g)1/2 = 1,08 c //ответ

Затухающие колебания
Сила вязкого трения Fтр = -βv
mx” = - kx – βv ⇨ mx” + βv + kx = 0 ⇨
x” + 2γx’ + ω02 x = 0 - дифференциальное уравнение колебаний с затуханием;
γ = β/2m – коэффициент затухания
ω02 = k/m – собственная частота
если γ < ω0,то
x = а0e-γtcos(ωt + φ0),
ω = (ω02 – γ2)1/2 – частота затухающих колебаний; а0e-γt – амплитуда затухающих колебаний

Характеристики затухающих колебаний
Время релаксации τ – это время, за которое амплитуда колебаний уменьшается в e раз:
τ = 1/ γ
Логарифмический декремент затухания:
λ = ln[a(t)/a(t + T)] = γT = T/τ
Число колебаний, за которое амплитуда уменьшается в e раз
Ne = τ/T = 1/λ
Слабое затухание Ne = τ/T = ω/2πγ >> 1 ⇨
γ << ω ≈ ω0

Диссипация энергии. Добротность
dE/dt = -βv2 - мощность силы трения
dE/dt = -βv2 = -(2β/m) (mv2/2) = - 4γK
Слабое затухание: γ << ω0 ⇨
= ½ E ⇨
d
/dt = - 2γ
⇨ E = E0e-2γt
Убыль энергии за период ΔЕT = 2γTE
Убыль энергии при изменении фазы на 1 рад:
ΔЕ = ΔЕT/2π = (2γ/ω)E0
Добротность:
Q = E/ΔЕ = ω/2γ = πNe

Задача 10.2
Зная период колебаний T и время уменьшения амплитуды колебаний в 2 раза τ, найдите добротность колебательной системы.
Решение:
A = A0e-γt → γ = ℓn2/τ →
Q = ω0/2γ = πτ/Tℓn2 //ответ

Задача 10.4
Свободные колебания математического маятника массы m, длиной ℓ испытывают затухание из-за трения о воздух. Сила трения пропорциональна скорости с коэффициентом пропорциональности β. Для поддержания колебаний маятник раскачивают периодическими толчками — один раз за период в момент максимального отклонения маятника ему сообщают дополнительную скорость u. Найдите значение u, при котором амплитуда колебаний A маятника будет стационарна, и нарисуйте фазовую траекторию для этого случая.

Решение 10.4
A = A0e-γt → ΔA = A0γT → ΔE = kA0ΔA = mu2/2 → u2 = 2ω02A0ΔA = 2ω02A02γT = 4πγω0A02 = 2πβω0A02/m →
u = A0(2π ω0 β/m) (ω0 = (g/ℓ)1/2) //ответ
Энергетический подход:
ΔW = 2πW/Q = 2πkA22γ/ω0 = 2πkA2β/mω0 = 2πω0A2β = mu2/2 → u = A0(2π ω0 β/m) //ответ
Фазовая траектория: ΔA/A0 = 2γT → u/v0 = (2* 2γT)1/2 → u = A0(2π ω0 β/m) //ответ

Вынужденные колебания. Векторные диаграммы. Резонанс
mx” + βv + kx = Fcosωt ⇨
x” + 2γx’ + ω02x = fcos ωt, f = F/m
Вынужденные колебания ищем в виде:
x = Bcos(ωt + φ)
Векторная диаграмма:
x = Acos (ωt + φ0) проекция на ось OX радиус-вектора длиной A, вращающегося против часовой стрелки с угловой скоростью ω от начального положения φ0

Вынужденные колебания. Векторные диаграммы. Резонанс
Из векторной диаграммы:
амплитуда
B = f/((ω2 – ω02)2 + 4γ2ω2)1/2
Фаза
tg φ = 2γω/(ω02– ω2)
В резонансе (при малых γ)
Bmax ≈ B(ω0) = f/2γω0 ⇨ Bmax/Bстат = ω0/2γ = Q
Вблизи резонанса:
B = Bmaxγ/((ω – ω0)2 + γ2)1/2 ⇨ ширина резонансной кривой ΔΩ = 2γ

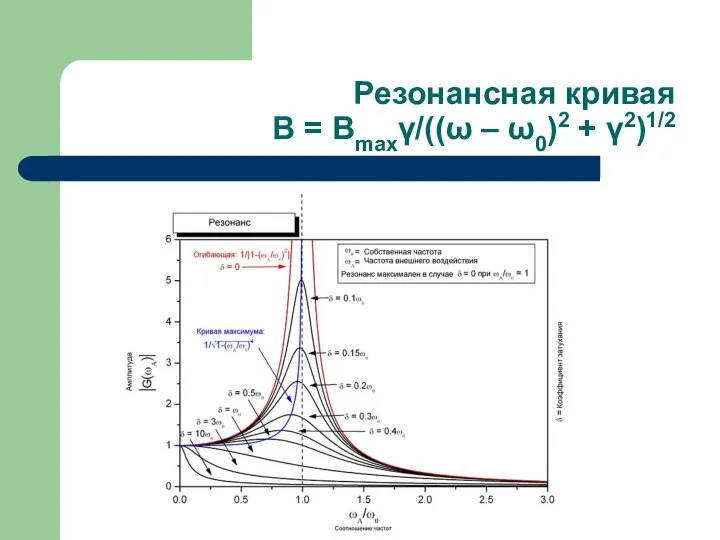
Резонансная кривая
B = Bmaxγ/((ω – ω0)2 + γ2)1/2

Параметрический резонанс
Параметрический резонанс - возбуждение незатухающих колебаний периодическим изменением параметров колебательной системы
Пример: маятник с изменяющейся длиной (качели)
Работа против тяжести:
A1 = mgΔh(1 - cos φ0) ≈ ½ mgΔhφ02 = ½ mv02 Δh/L
Работа против центробежной силы:
A2 = mv02Δh/L
приращение энергии за период:
ΔE = 2(A1 + A2) = 6 Δh/L mv02/2
dE/dt = 6 Δh/L E/T = E/τ ⇨ E = E0et/τ

Ангармонический математический маятник
½кθ2 + ½ μθ’2 = const ⇨ θ” + ω02 θ = 0 – линеаризованное уравнение
θ” + ω02sinθ = 0 – нелинеаризованное ангармоническое уравнение;
T = T0(1 + θ02/16 + 9θ04/64 + …) – период зависит от амплитуды θ0

Волновое уравнение. Скорость упругих волн в тонком стержне
∂2x/∂t2 = v2 ∂2x/∂z2
общее решение волнового уравнения:
x = x(t – z/v) + x(t + z/v)
Относительная деформация ε = ∂x/∂z
Закон Гука σ = Eε ⇨
Закон Ньютона для участка стержня Δz:
Δm∂2x/∂t2 = F ⇨
ρSΔz ∂2x/∂t2 = (σ(z + Δz) - σ(z))S = ES∂ε/∂z ⇨
∂2x/∂t2 = (E/ρ) ∂2x/∂z2 ⇨ v = (E/ρ)1/2

Численные примеры (сталь)
Модуль Юнга: E0 = 2 1011 Н/м2 = 2 Мбар; коэффициент Пуассона μ = 0,3; плотность ρ = 7,8 г/см3 ⇨ v = (E0/ρ)1/2 = 5064 м/с (табл. v = 5150 м/с)
В толстом стержне:
Модуль одностороннего сжатия
E = E0(1 – μ)/(1 + μ)(1 - 2μ) = 1,35E0 ⇨
vII = (E/ρ)1/2 = (1,35)1/2v = 5884 м/с (табл. v = 5900 м/с)
Поперечный звук: v┴ = (G/ρ)1/2,
G = E0/2(1 + μ) = E0/2,6 – модуль сдвига ⇨
v┴ = v/(2,6)1/2 = 3140 м/с (табл. v┴ = 3100 м/с)

Численные примеры (алюминий)
Модуль Юнга: E0 = 0,705 1011 Н/м2 = 0,705 Мбар; коэффициент Пуассона μ = 0,345;
плотность ρ = 2,7 г/см3
скорость звука в тонком стержне
v = (E0/ρ)1/2 = 5110 м/с (табл. v = 5240 м/с (2,5%))
В толстом стержне:
Модуль одностороннего сжатия
E = E0(1 – μ)/(1 + μ)(1 - 2μ) = 1,57E0 ⇨
vII = (E/ρ)1/2 = (1,57)1/2v = 6403 м/с (табл. v = 6400 м/с)
Поперечный звук: v┴ = (G/ρ)1/2,
G = E0/2(1 + μ) = E0/2,69 – модуль сдвига ⇨
v┴ = v/(2,69)1/2 = 3115 м/с (табл. v┴ = 3100 м/с)

Скорость звука в жидкостях и газах
В газе Δz/z = ΔV/V = Δp/Е ⇨ модуль упругости в жидкости
E = dp/(dV/V) = dp/(dρ/ρ) коэффициент всестороннего сжатия.
Скорость звука в жидкости
v = (dp/dρ)1/2
Избыточное давление
Δp = Eε = Eερ/ρ = ρuv

Численные примеры (вода, воздух)
v = (dp/dρ)1/2
Вода:
v = (K/ρ)1/2 K = Vdp/dV - модуль всестороннего сжатия воды:
К = dp/(dV/V) = 2,14*104 Н/м2
v = (K/ρ)1/2 = 1463 м/с (табл. v = 1484 м/с (1,3%))
Воздух:
изотермический звук:
vT = (dp/dρ)Т1/2 = (p/ρ)1/2 = 280 м/с
Адиабатический звук:
vs = (dp/dρ)s1/2 = (γp/ρ)1/2 = (1,4)1/2 vT = 330 м/с

Скорость волны в гибком шнуре. Струна
v = (T/ρl)1/2 – скорость распространения упругих волн небольшой амплитуды в натянутой струне;
T – натяжение струны
ρl – погонная плотность
Вывод:
ρl Δz ∂2x/∂t2 = T(sinα(z+Δz) - (sinα(z)) ⇨ ∂2x/∂t2 = (T/ρl)∂2x/∂z2

Энергия упругой волны. Амплитуда давления в звуковой волне.
Плотность кинетическая энергии:
wk = ρu2/2 = ρx’2/2 = ½ ρA2ω2sin2(ωt – kz)
Плотность упругой энергии:
wП = Eε2/2 = ½ ρA2ω2sin2(ωt – kz)
Полная энергия
w = wk + wП = ρx’2/2 + Eε2/2 = ρA2ω2sin2(ωt – kz)
Для гармонической волны:
= ½ ρA2ω2 =
Поток энергии, или интенсивность:
I = ½ ρA2ω2v
I = 2
v = (Eεm2/2) v = (Δp)2/2vρ ⇨
Δp = (2Iρv)1/2