Механические колебания. Лекция 8

Виды и признаки колебаний
Колебания делятся на механические и электромагнитные (электромеханические комбинации)
Для колебаний характерно превращение одного вида энергии в другую – кинетической в потенциальную, магнитной в электрическую и т.д.
Колебательным движением (или просто колебанием) называются процессы, повторяющиеся во времени.

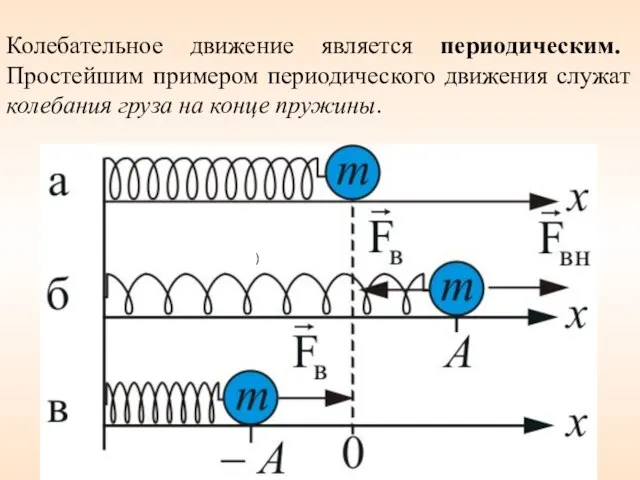
Колебательное движение является периодическим. Простейшим примером периодического движения служат колебания груза на конце пружины.
)

Три признака колебательного движения:
повторяемость (периодичность) – движение по одной и той же траектории туда и обратно;
ограниченность пределами крайних положений;
действие силы, описываемой функцией F = – kx.

Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Простейшим типом периодических колебаний являются так называемые гармонические колебания.
Любая колебательная система, в которой возвращающая сила прямо пропорциональна смещению, взятому с противоположным знаком (например, F = – kx), совершает гармонические колебания.
Саму такую систему часто называют гармоническим осциллятором.

Различные периодические процессы (повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний.
Периодический процесс можно описать уравнением:
Колебания называются гармоническими, если зависимость некоторой величины имеет вид
или

Расстояние груза от положения равновесия до точки, в которой находится груз, называют смещением x.
Максимальное смещение – наибольшее расстояние от положения равновесия – называется амплитудой и обозначается, буквой A.
определяет смещение x в данный момент времени t и называется фазой колебания.
называется начальной фазой колебания при t=0
Параметры гармонических колебаний
.

Частота колебаний ν определяется, как число полных колебаний в 1 секунду. Частоту, измеряют в герцах (Гц):
1 Гц = 1 колебание в секунду.
Период колебаний Т – минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание

ω – циклическая (круговая) частота – число полных колебаний за 2π секунд.
Фаза φ не влияет на форму кривой х(t), а влияет лишь на ее положение в некоторый произвольный момент времени t.
Гармонические колебания являются всегда синусоидальными.
Частота и период гармонических колебаний не зависят от амплитуды.

– амплитуда скорости;
– амплитуда ускорения.
Смещение описывается уравнением
тогда, по определению:
скорость
ускорение

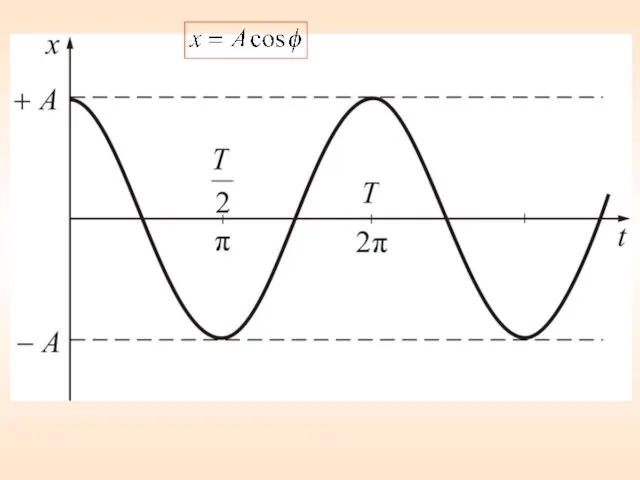
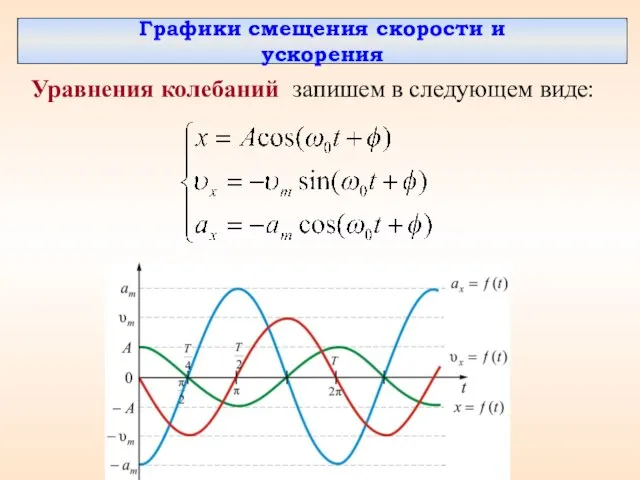
Графики смещения скорости и ускорения
Уравнения колебаний запишем в следующем виде:

Скорость колебаний тела максимальна и равна амплитуде скорости в момент прохождения через положение равновесия (x=0).
При максимальном смещении ( ) скорость равна нулю.
Ускорение равно нулю при прохождении телом положения равновесия и достигает наибольшего значения, равного амплитуде ускорения при наибольших смещениях.

Основное уравнение динамики гармонических
колебаний
Исходя из второго закона, , можно записать
сила F пропорциональна х и всегда направлена к положению равновесия (поэтому ее и называют возвращающей силой).
Примером сил являются упругие силы. Силы же имеющие иную природу называются квазиупругими. Квазиупругая сила
где k – коэффициент квазиупругой силы.

Получим основное уравнение динамики гармонических колебаний, вызываемых упругими силами:
или ; , тогда
Решение этого уравнения всегда будет выражение вида
Основное уравнение динамики гармонических колебаний

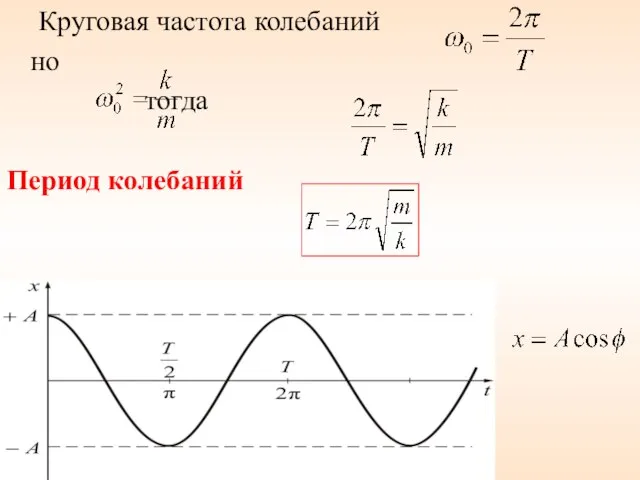
Круговая частота колебаний
но
тогда
Период колебаний

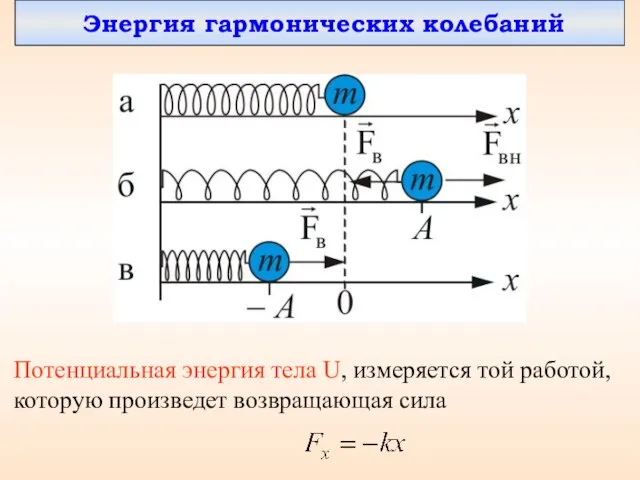
Энергия гармонических колебаний
Потенциальная энергия тела U, измеряется той работой, которую произведет возвращающая сила

, отсюда
Кинетическая энергия
Полная энергия:
Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания.
Потенциальная энергия

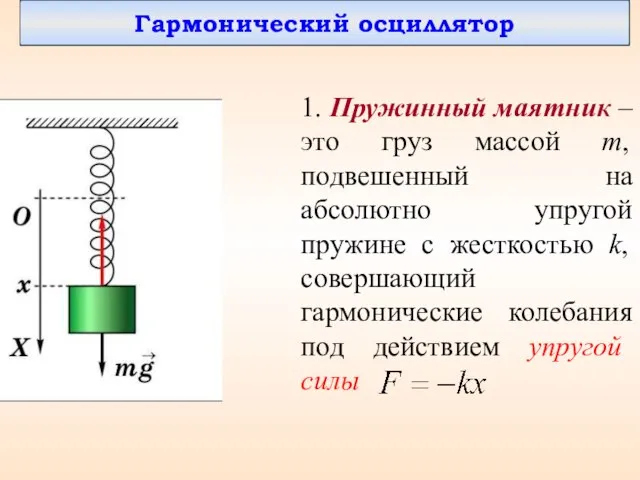
Гармонический осциллятор
1. Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине с жесткостью k, совершающий гармонические колебания под действием упругой силы

или
циклическая частота ω период Т
Из второго закона Ньютона F = mа; или F = - kx
получим уравнение движения маятника:
Решение этого уравнения – гармонические колебания вида:

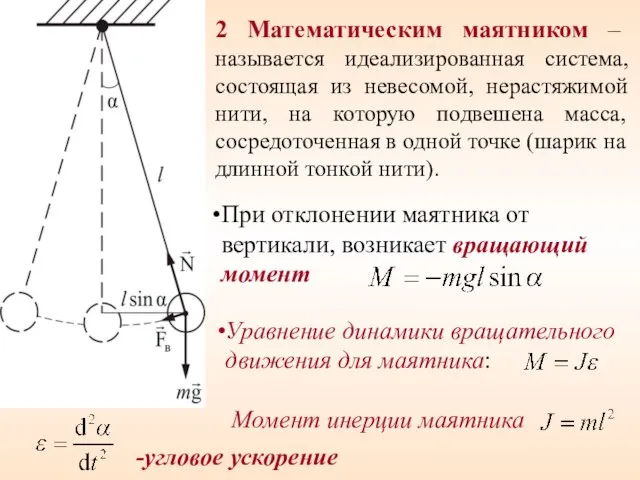
2 Математическим маятником – называется идеализированная система, состоящая из невесомой, нерастяжимой нити, на которую подвешена масса, сосредоточенная в одной точке (шарик на длинной тонкой нити).
При отклонении маятника от вертикали, возникает вращающий момент
Уравнение динамики вращательного движения для маятника:
Момент инерции маятника
-угловое ускорение

Тогда
, или
Обозначим
:
- Это уравнение динамики гармонических колебаний.
Решение уравнения имеет вид:
Т – зависит только от длины маятника и ускорения свободного падения.
Уравнение движения маятника

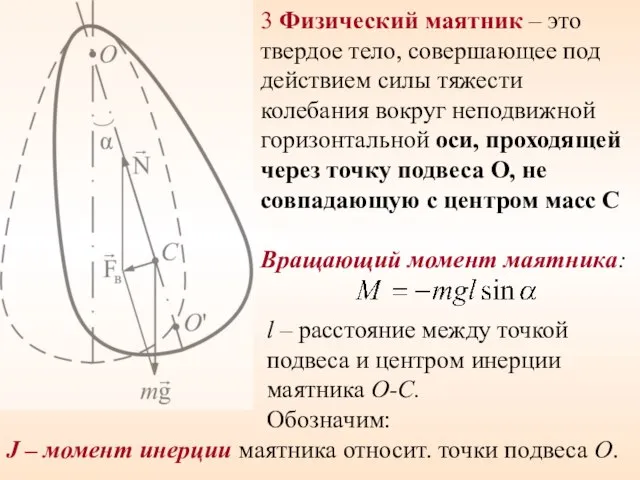
3 Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку подвеса О, не совпадающую с центром масс С
Вращающий момент маятника:
l – расстояние между точкой подвеса и центром инерции маятника О-С.
Обозначим:
J – момент инерции маятника относит. точки подвеса O.

- угловое ускорение, тогда
Уравнение динамики вращательного движения
– приведенная длина физического маятника – это длина такого математического маятника, период колебания которого совпадает с периодом колебаний данного физического маятника.

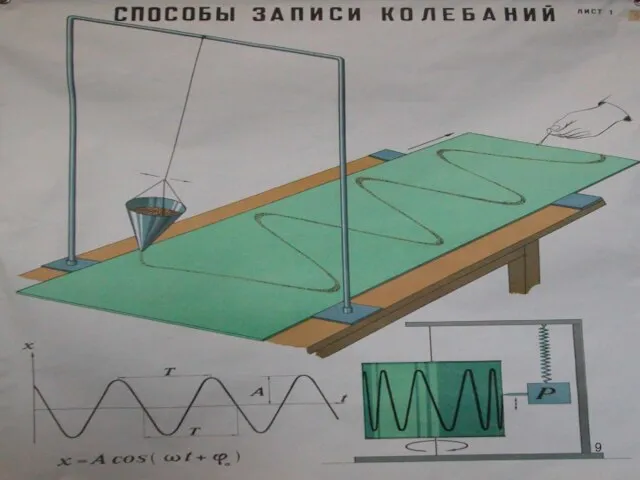
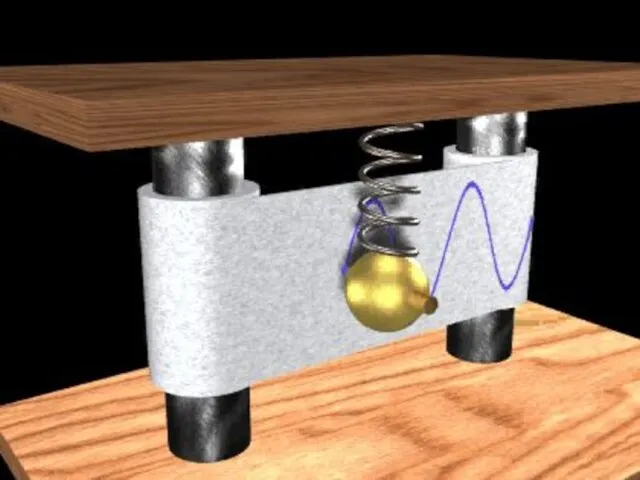
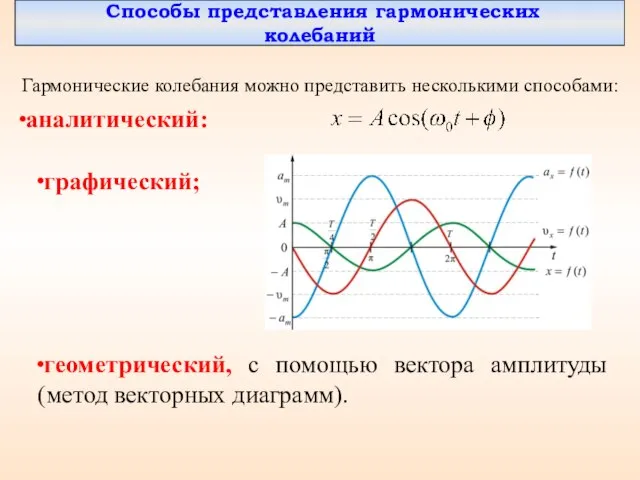
Способы представления гармонических колебаний
Гармонические колебания можно представить несколькими способами:
аналитический:
графический;
геометрический, с помощью вектора амплитуды (метод векторных диаграмм).

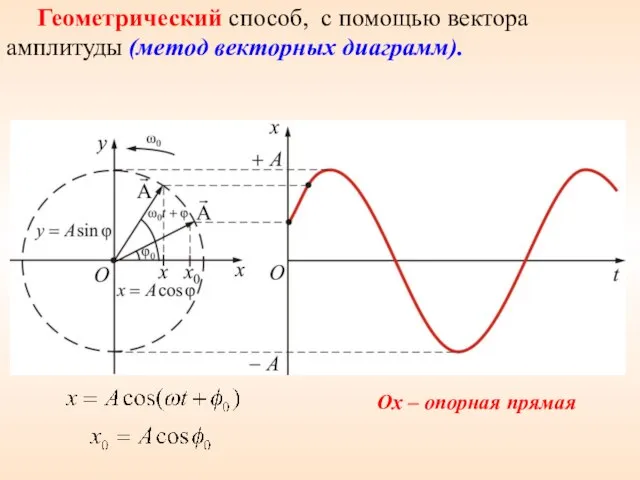
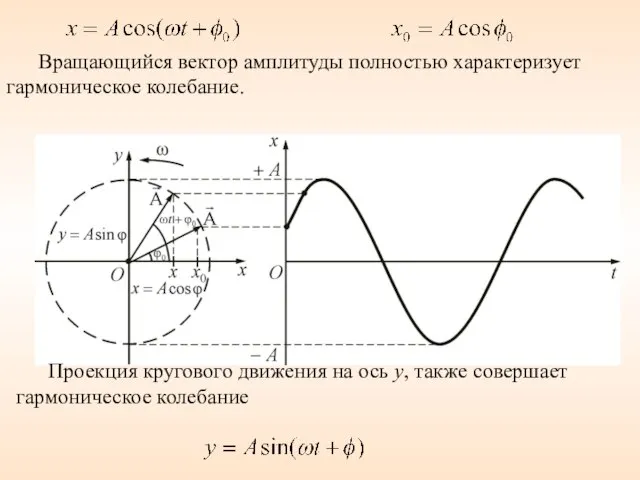
Геометрический способ, с помощью вектора амплитуды (метод векторных диаграмм).
Ox – опорная прямая

Вращающийся вектор амплитуды полностью характеризует гармоническое колебание.
Проекция кругового движения на ось у, также совершает гармоническое колебание

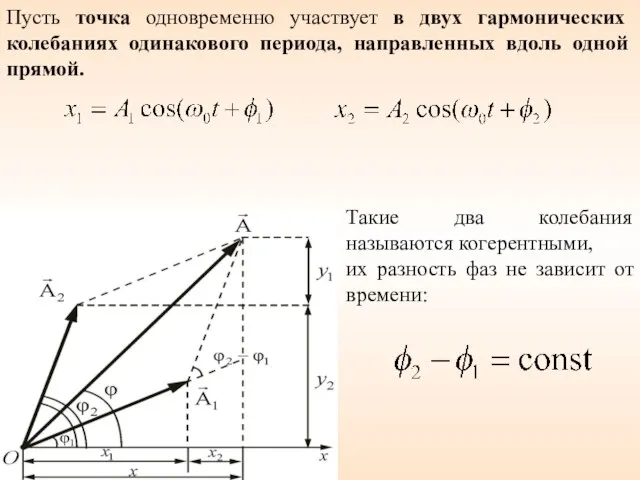
Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой.
Такие два колебания называются когерентными,
их разность фаз не зависит от времени:

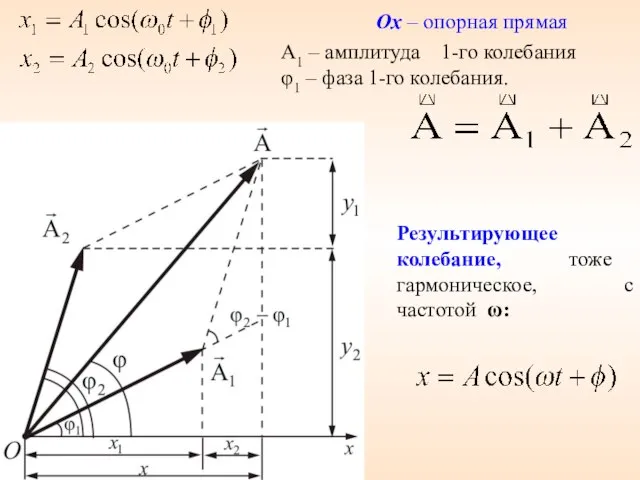
Ox – опорная прямая
A1 – амплитуда 1-го колебания
φ1 – фаза 1-го колебания.
Результирующее колебание, тоже гармоническое, с частотой ω:

По правилу сложения векторов найдем суммарную амплитуду, результирующего колебания:
Начальная фаза определяется из соотношения
Амплитуда А результирующего колебания зависит от разности начальных фаз

Сложение взаимно перпендикулярных колебаний
В результате получили уравнение эллипса с произвольно расположенными осями

Свободные затухающие механические колебания
Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний уменьшается.
Сила трения (или сопротивления)
где r – коэффициент сопротивления,

Второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x
где kx – возвращающая сила, – сила трения.
Введем обозначения
)

Найдем частоту колебаний ω.
;
;
Условный период
Решение уравнения имеет вид

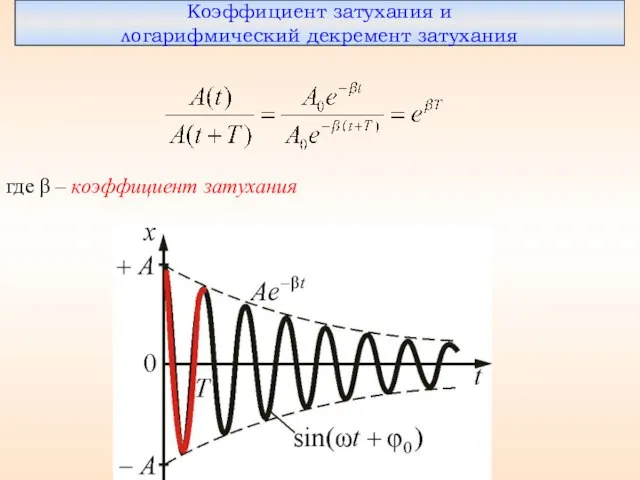
Коэффициент затухания и
логарифмический декремент затухания
где β – коэффициент затухания

Логарифмическим декрементом затухания называется натуральный логарифм отношения амплитуд, следующих друг за другом через период Т.
Следовательно, коэффициент затухания β – есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз,
τ – время релаксации.

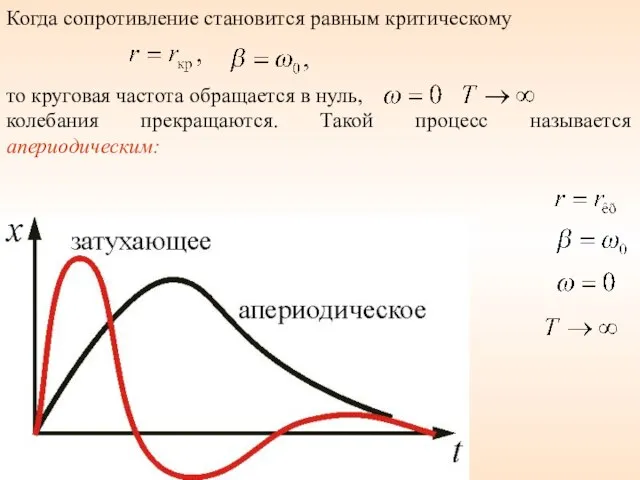
Когда сопротивление становится равным критическому
то круговая частота обращается в нуль,
колебания прекращаются. Такой процесс называется апериодическим:

Вынужденные механические колебания
Рассмотрим систему, на которую кроме упругой силы (– kx) и сил сопротивления (– rυ) действует добавочная периодическая сила F – вынуждающая сила:
– основное уравнение колебательного процесса, при вынужденных колебаниях

Уравнение установившихся вынужденных колебаний
Задача найти амплитуду А и разность фаз φ между смещением вынужденных колебаний и вынуждающей силой.
– амплитуда ускорения;
– амплитуда скорости;
– амплитуда смещения;
– амплитуда вынуждающей силы
Введем обозначения:

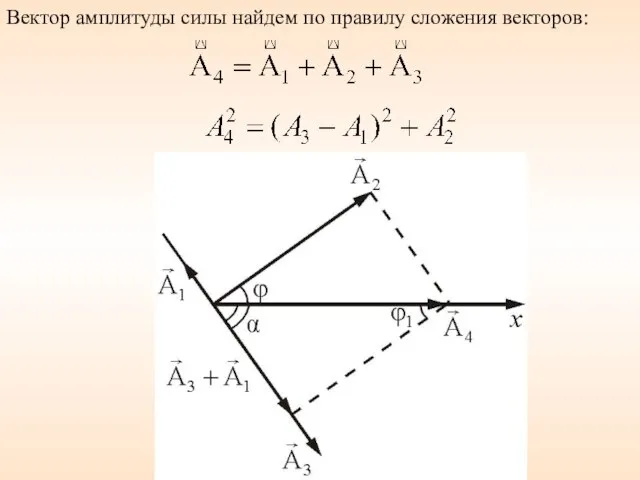
Вектор амплитуды силы найдем по правилу сложения векторов:

1)
(частота вынуждающей силы равна нулю)
– статическая амплитуда, колебания не совершаются.
2)
(затухания нет). С увеличением ω (но при
), амплитуда растет и при
, амплитуда
резко возрастает (
). Это явление называется
– резонанс. При дальнейшем увеличении (
)
амплитуда опять уменьшается.
3) – резонансная частота

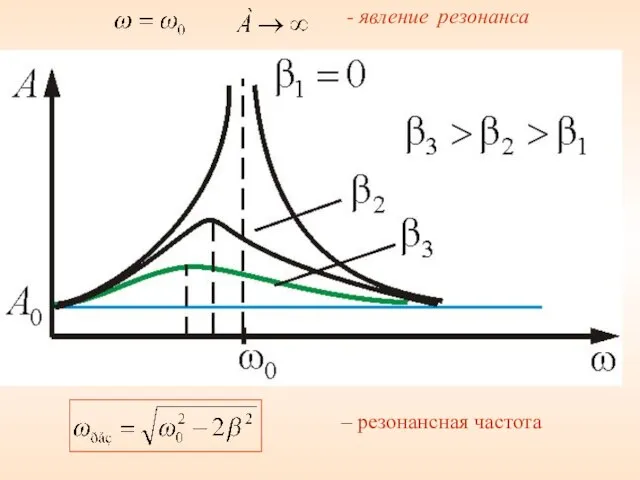
- явление резонанса
– резонансная частота

– резонансная частота.
Явление возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к называется резонансом.
С увеличением коэффициента затухания β явление резонанса проявляется все слабее и исчезает при